测地距离

转载自：http://lemonc.me/average-geodesic-distance.html 作者：LEEMANCHIU

Geodesic Distane

"geodesic"（测地线）一词来源于 geodesy（测地学），是一门测量地球大小和形状的学科。

就从 geodesic 的本意来说，就是地球表面两点之间的最短路径，因此 Geodesic Distance 最初是指地球表面两点之间的最短距离，但随后这一概念便被推广到了数学空间的测量之中。

在图论中，Geodesic Distance 就是图中两节点的最短路径的距离。这与我们平时在几何空间通常用到的 Euclidean Distance（欧氏距离），即两点之间的最短距离是不同。

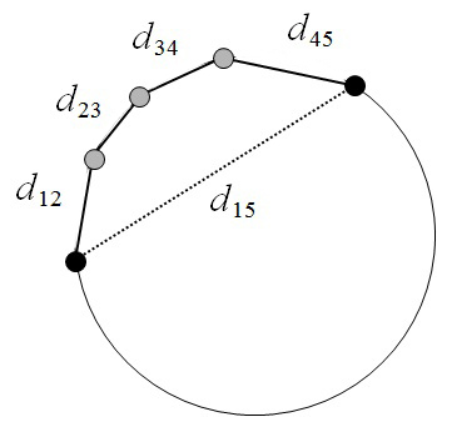
欧式距离：\(d_{15}\)

测地距离：\(d_{12}+d_{23}+d_{34}+d_{45}\)(在曲面上从A点走到B点（不允许离开曲面）的最短距离)

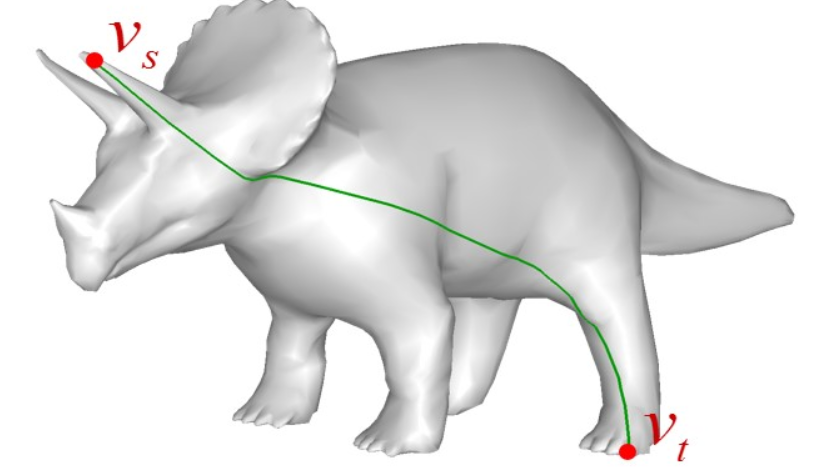
在三维网格中，Geodesic Distance 就是两顶点沿网格表面最短路径的距离。

对于计算三维点云中两点的 Geodesic Distance，首先要利用点云中所有点构建出一个类似于网格的表面结构的图，随后通过找到两点在图中的最短路径，再去计算 Geodesic Distance。

Average Geodesic Distance

给定一个点，计算该点到剩余所有点的 Geodesic Distance 的平均值。用这个 Average Geodesic Distance 作为一个三维点的几何特征时，越靠近中心部位的点的值会越低，而边缘末端的点的值会相对更高，所以很容易通过此特征捕获到这两种类型的区域。

这看似简单的算法原理在实际的计算中还是相当耗时的，会随着三维点数的增加，耗时呈指数级的增长。但由于实际中往往并不需要用到非常精确的 Geodesic Distance。

伪代码：

For each point {
    double totalDistance = 0;
    int totalCount = 0;
    For each otherPoint {
        FindShortestPaths();
        double geodesicDistance = ComputeShortestDistance();
        totalDistance += geodesicDistance;
        ++totalCount;
    }
    double averageGeodesicDistance = totalDistance / totalCount;
    averageGeodesicDistance = normalize(averageGeodesicDistance);
}