卷积扩展知识

分治卷积

问题

已知$g(i)$的各项函数值

$f(i)=\sum_{j=1}^i g(j)*f(i-j)$

求$f(i)$的各项函数值

解法

考虑cdq分治思想

每次二分，先把左边的f(i)计算出来， 然后计算左边的f(i)对右边的贡献，再继续累积右边的贡献

二分到达边界时，表明这个点的函数值已经统计完毕

同理，当二分完一个区间时，表明该区间所有函数值已计算完毕

举例：

假设一开始知道f(0)的值

二分到区间0~1时，左边区间0~0已知，那么可以用f(0)计算f(1),另外f(1)除了f(0)无其他贡献来源，所以f(1)计算完毕

（绿色表示计算完成，黄色表示正在计算中）

回退到0~2时，0~1已知，可以用于计算f(1)~f(2)

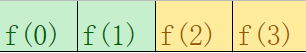
 进入2~2，到达边界，f(2)计算完成，回退，累计f(2)对f(3)的贡献

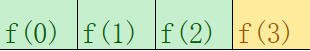
 进入3~3，到达边界，f(3)计算完成，回退至0~7区间，累计f(0~3)对f(4~7)的贡献

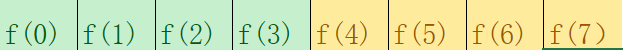
 之后以此类推即可

代码

代码中有些细节解释

#include<bits/stdc++.h>
using namespace std;
#define N 300000
#define int long long
int g[N],f[N],res[N],ind,rev[N],ta[N],tb[N];
const int p=998244353;
int qpow(int aa,int bb)
{
	int res=1;
	aa%=p;
	while(bb)
	{
		if(bb&1) res*=aa,res%=p;
		aa*=aa,aa%=p;
		bb>>=1ll;
	}
	return res;
}
void ntt(int arr[],int g,int n)
{
	for(int i=1;i<=n;i++)
	{
		if(i<rev[i]) swap(arr[i],arr[rev[i]]);
	}
	for(int len=1;len<n;len*=2)
	{
		int offect=qpow(g,(p-1)/(len<<1));
		for(int i=0;i<n;i+=len*2)
		{
			for(int j=0,g1=1;j<len;j++,g1=g1*offect%p)
			{
				int t=arr[i+j];
				arr[i+j]=(t+g1*arr[i+j+len]%p)%p;
				arr[i+j+len]=(t-g1*arr[i+j+len]%p+p)%p;
			}
		}
	}
}
void mul(int ans[],int len)
{
	int x=0,y=1;
	while(y<=len) x++,y<<=1;
	len=y;
	for(int i=0;i<=len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(x-1));
	ntt(ta,3,len);
	ntt(tb,3,len);
	for(int i=0;i<=len;i++) ans[i]=ta[i]*tb[i]%p;
	int inv=qpow(3,p-2);
	ntt(ans,inv,len);
	//ntt(a,inv,len,p);
	//ntt(b,inv,len,p);
	int z=qpow(len,p-2);
	for(int i=0;i<=len;i++) ans[i]=ans[i]*z%p,ta[i]=tb[i]=0;
}
void divide(int l,int r)
{
	if(l==r) return;
	int mid=(l+r)/2;
	divide(l,mid);
	memset(res,0,16*(r-l+1));
	memcpy(ta,f+l,8*(mid-l+1));
	memcpy(tb,g,8*(r-l+1));//实际是f(l~mid)*g(mid+1~r) 但为了凑足g的次数还是从g(1)开始 
	mul(res,r-l+1);//乘出来的res应该是r-l+1+mid-l+1项的，但我们只关心mid+1~r项，所以只需要计算1~r-l+1项就行了 
	for(int i=mid+1;i<=r;i++) f[i]+=res[i-l],f[i]%=p; 
	divide(mid+1,r);
}
signed main()
{
	int n;
	cin>>n;
	n--; 
	for(int i=1;i<=n;i++) scanf("%lld",&g[i]);
	f[0]=1;
	int t=1;
	while(t<n) t<<=1,ind++;
	divide(0,t-1);
	for(int i=0;i<=n;i++) printf("%lld ",f[i]);
}

　　

任意模数卷积

如果题目的模数不是NTT模数，甚至没有模数，并且值域范围很大，fft会掉精度

介绍两种办法

拆系数fft

将多项式系数拆为$a_i=b_i*m+c_I$，m是阈值，一般取1e5,这样如果$a_i<=10^9，则b_i,c_i<=10^5$，乘起来不会太大

这样$f(x)=f_1(x)*m+f_2(x)$

然后$f(x)*g(x)=f_1(x)*g_1(x)*m^2+(f_1(x)*g_2(x)+f_2(x)*g_1(x))*m+f_2(x)*g_2(x)$

做四次fft即可

三模数ntt

 代码

#include<bits/stdc++.h>
using namespace std;
#define N 300000
#define int long long
int ta[N],tb[N],a[N],b[N],ans[5][N],p[4]={0,469762049,998244353,1004535809},rev[N];
int fmul(int a, int b, int mod) {//用于计算会爆long long的乘法
    a %= mod, b %= mod;
    return ((a * b - (int)((int)((long double)a / mod * b + 1e-3) * mod)) % mod + mod) % mod;
}
int qpow(int aa,int bb,int pp)
{
	int res=1;
	aa%=pp;
	while(bb)
	{
		if(bb&1) res*=aa,res%=pp;
		aa*=aa,aa%=pp;
		bb>>=1ll;
	}
	return res;
}
void ntt(int arr[],int g,int n,int p)
{
	for(int i=1;i<=n;i++)
	{
		if(i<rev[i]) swap(arr[i],arr[rev[i]]);
	}
	for(int len=1;len<n;len*=2)
	{
		int offect=qpow(g,(p-1)/(len<<1),p);
		for(int i=0;i<n;i+=len*2)
		{
			for(int j=0,g1=1;j<len;j++,g1=g1*offect%p)
			{
				int t=arr[i+j];
				arr[i+j]=(t+g1*arr[i+j+len]%p)%p;
				arr[i+j+len]=(t-g1*arr[i+j+len]%p+p)%p;
			}
		}
	}
}
int len=1,l=0;
void mul(int a[],int b[],int ans[],int n,int p)
{
	
	for(int i=0;i<=len;i++)
	{
		rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
	}
	ntt(a,3,len,p);
	ntt(b,3,len,p);
	for(int i=0;i<=len;i++) ans[i]=a[i]*b[i]%p;
	int inv=qpow(3,p-2,p);
	ntt(ans,inv,len,p);
	//ntt(a,inv,len,p);
	//ntt(b,inv,len,p);
	for(int i=0;i<=len;i++) ans[i]=ans[i]*qpow(len,p-2,p)%p;
}
signed main()
{
	int n,m,p0;
	cin>>n>>m>>p0;
	while(len<n+m+1) len<<=1,l++;
	for(int i=0;i<=n;i++) scanf("%lld",&a[i]);
	for(int i=0;i<=m;i++) scanf("%lld",&b[i]);
	for(int i=1;i<=3;i++)
	{
		//memset(ta,0,sizeof(ta));
		//memset(tb,0,sizeof(tb));
		for(int j=0;j<=len;j++) ta[j]=a[j];
		for(int j=0;j<=len;j++) tb[j]=b[j];
		mul(ta,tb,ans[i],n+m+1,p[i]);
	}
	int pn=p[1]*p[2],inv1=qpow(p[2],p[1]-2,p[1]),inv2=qpow(p[1],p[2]-2,p[2]),inv3=qpow(pn,p[3]-2,p[3]);
	for(int i=0;i<=n+m;i++)
	{
		ans[4][i]=(fmul(ans[1][i]*p[2],inv1,pn)+fmul(ans[2][i]*p[1],inv2,pn))%pn;
		int t=(ans[3][i]-ans[4][i]%p[3]+p[3])%p[3]*inv3%p[3];
		ans[0][i]=(pn%p0*t%p0+ans[4][i])%p0;
		printf("%lld ",(ans[0][i]+p0)%p0);
	}

}