力扣 - 72. 编辑距离

目录

• 题目
• 思路
• 题解
• 代码实现
  • 自顶向下（递归）
  • 自底向上（动态规划）
  • 优化版，空间复杂度仅为O(n)，n为目标字符串的长度

题目

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

思路

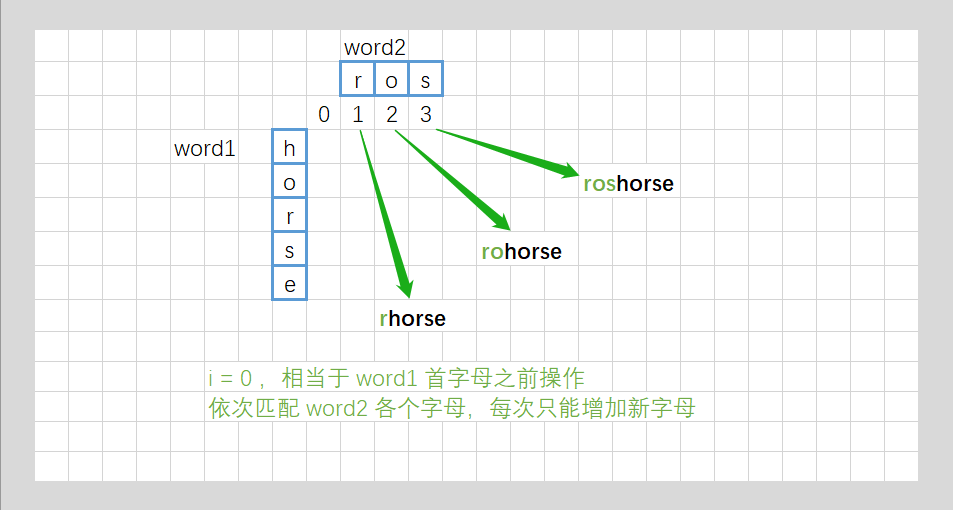
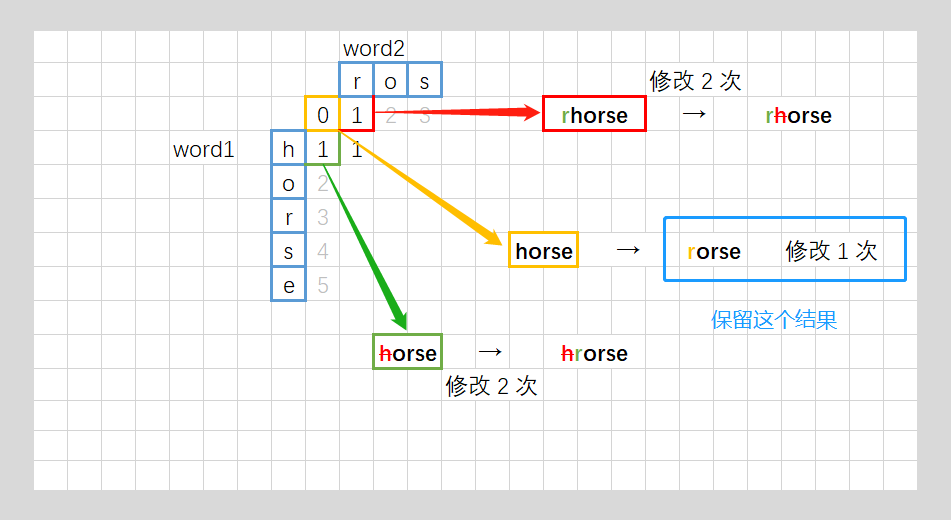
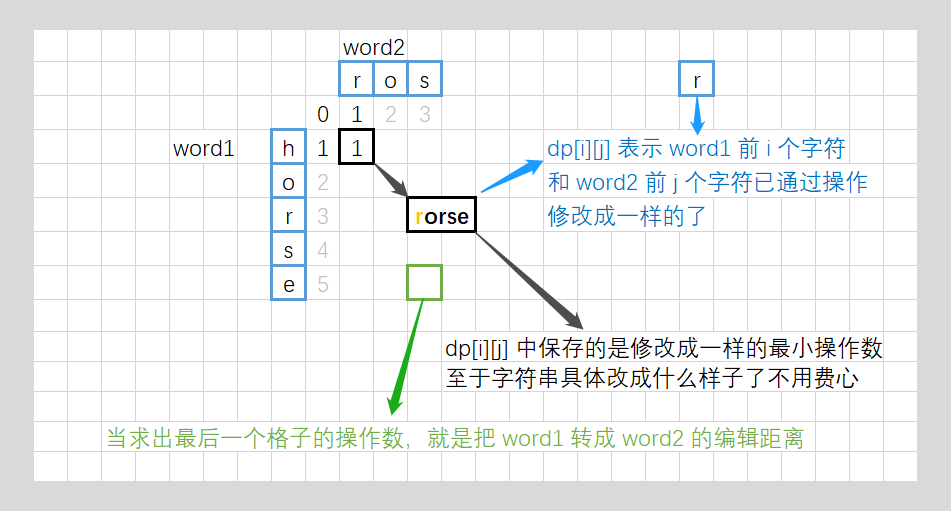
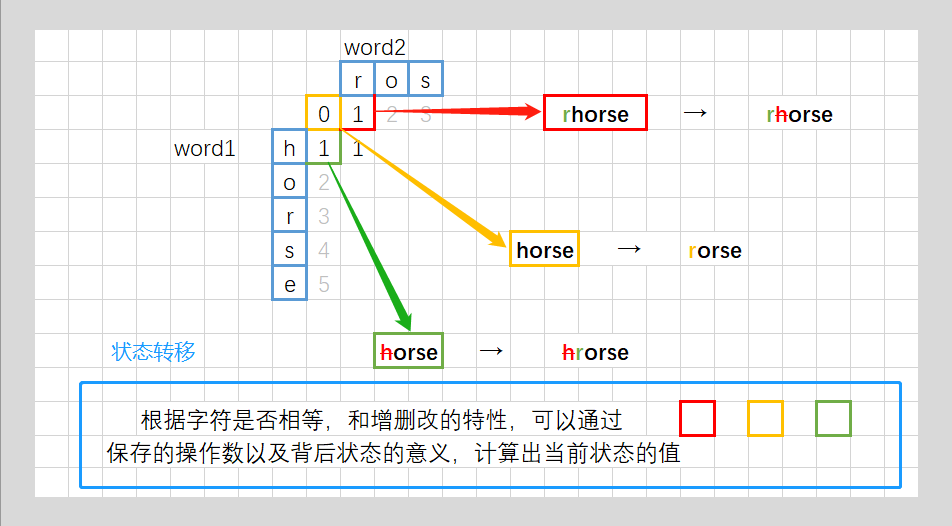
• 将上边界初始化为0 1 2 3 4 ··· 是因为在word1的前边插入字符，插入一个就代表增加一；左边界也是一样的，向下一格就代表删去一个字符，可得出：
  • 如果把字符 word1[i] 替换成与 word2[j] 相等，则有 dp[i] [j] = dp[i-1] [j-1] + 1;
  • 如果在字符串 word1末尾插入一个与 word2[j] 相等的字符，则有 dp[i] [j] = dp[i] [j-1] + 1;
  • 如果把字符 word1[i] 删除，则有 dp[i] [j] = dp[i-1] [j] + 1;
  • 那么我们应该选择一种操作，使得 dp[i] [j] 的值最小，显然有dp[i] [j] = min(dp[i-1] [j-1]，dp[i] [j-1]，dp[[i-1] [j]]) + 1;
• 即如果相等就操作次数不变，和上一次一样；如果不相等的话，要插入，就dp[i][j] = dp[i][j-1] + 1、要删除，就dp[i][j] = dp[i-1][j] + 1、要替换，就dp[i][j] = dp[i-1][j-1] + 1

题解

作者：ikaruga 链接：https://leetcode-cn.com/problems/edit-distance/solution/edit-distance-by-ikaruga/ 来源：力扣（LeetCode）

代码实现

自顶向下（递归）

• 递归这个方法由于计算了太多的重叠子问题，导致超出时间限制

class Solution {
    public int minDistance(String word1, String word2) {
        return dp(word1.length()-1, word2.length()-1, word1, word2);
    }

    private int dp(int n1, int n2, String word1, String word2) {
        if (n1 == -1) return n2 + 1;
        if (n2 == -1) return n1 + 1;

        if (word1.charAt(n1) == word2.charAt(n2)) {
            return dp(n1 - 1, n2 - 1, word1, word2);
        } else {
            return Math.min(Math.min(dp(n1-1, n2, word1, word2), dp(n1, n2-1, word1, word2)), dp(n1-1, n2-1, word1, word2)) + 1;
        }
    }
}

自底向上（动态规划）

class Solution {
    public int minDistance(String word1, String word2) {
        int n1 = word1.length();
        int n2 = word2.length();

        int[][] dp = new int[n1+1][n2+1];
        for (int i = 1; i <= n1; i++) {
            dp[i][0] = i;
        }
        for (int i = 1; i <= n2; i++) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= n1; i++) {
            for (int j = 1; j <= n2; j++) {
                if (word1.charAt(i-1) == word2.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i][j-1], dp[i-1][j]), dp[i-1][j-1]) + 1;
                }
            }
        }
        return dp[n1][n2];
    }
}

优化版，空间复杂度仅为O(n)，n为目标字符串的长度

class Solution {
    public int minDistance(String word1, String word2) {
        int n1 = word1.length();
        int n2 = word2.length();

        // 使用一维数组来存储
        int[] dp = new int[n2 + 1];

        // 初始化
        for (int i = 0; i <= n2; i++) {
            dp[i] = i;
        }

        for (int i = 1; i <= n1; i++) {
            //在不断向后比较的时候，前面的也要实时更新
            int temp = dp[0];
            dp[0] = i;
            // 将每个字符进行比较
            for (int j = 1; j <= n2; j++) {
                // 记录左上角的数字
                int pre = temp;
                temp = dp[j];
                if (word1.charAt(i-1) == word2.charAt(j-1)) {
                    dp[j] = pre;
                } else {
                    dp[j] = Math.min(Math.min(dp[j-1], dp[j]), pre) + 1;
                }
            }
        }
        return dp[n2];
    }
}