ACM数论之旅7---欧拉函数的证明及代码实现(我会证明都是骗人的╮( ̄▽ ̄)╭)
欧拉函数,用φ(n)表示
欧拉函数是求小于等于n的数中与n互质的数的数目
辣么,怎么求哩?~(~o ̄▽ ̄)~o
可以先在1到n-1中找到与n不互质的数,然后把他们减掉
比如φ(12)
把12质因数分解,12=2*2*3,其实就是得到了2和3两个质因数
然后把2的倍数和3的倍数都删掉
2的倍数:2,4,6,8,10,12
3的倍数:3,6,9,12
本来想直接用12 - 12/2 - 12/3
但是6和12重复减了
所以还要把即是2的倍数又是3的倍数的数加回来 (>﹏<)
所以这样写12 - 12/2 - 12/3 + 12/(2*3)
这叫什么,这叫容斥啊,容斥定理听过吧
比如φ(30),30 = 2*3*5
所以φ(30) = 30 - 30/2 - 30/3 - 30/5 + 30/(2*3) + 30/(2*5) + 30/(3*5) - 30/(2*3*5)
但是容斥写起来好麻烦( ̄. ̄)
有一种简单的方法
φ(12) = 12*(1 - 1/2)*(1 - 1/3) = 12*(1 - 1/2 - 1/3 + 1/6)
φ(30) = 30*(1 - 1/2)*(1 - 1/3)*(1 - 1/5) = 30*(1 - 1/2 - 1/3 - 1/5 + 1/6 + 1/10 + 1/15 - 1/30)
你看( •̀∀•́ ),拆开后发现它帮你自动帮你容斥好
所以φ(30)的计算方法就是先找30的质因数
分别是2,3,5
然后用30* 1/2 * 2/3 * 4/5就搞定了
顺便一提,phi(1) = 1
代码如下:
1 //欧拉函数 2 int phi(int x){ 3 int ans = x; 4 for(int i = 2; i*i <= x; i++){ 5 if(x % i == 0){ 6 ans = ans / i * (i-1); 7 while(x % i == 0) x /= i; 8 } 9 } 10 if(x > 1) ans = ans / x * (x-1); 11 return ans; 12 }
(phi就是φ的读音)
机智的代码,机智的我(。・`ω´・)
这个的复杂度是O(√n),如果要你求n个数的欧拉函数,复杂度是O(n√n),这也太慢了
有更快的方法
跟埃筛素数差不多
1 #include<cstdio> 2 const int N = 100000 + 5; 3 int phi[N]; 4 void Euler(){ 5 phi[1] = 1; 6 for(int i = 2; i < N; i ++){ 7 if(!phi[i]){ 8 for(int j = i; j < N; j += i){ 9 if(!phi[j]) phi[j] = j; 10 phi[j] = phi[j] / i * (i-1); 11 } 12 } 13 } 14 } 15 int main(){ 16 Euler(); 17 }
(Euler就是欧拉)
另一种,比上面更快的方法
需要用到如下性质
p为质数
1. phi(p)=p-1 因为质数p除了1以外的因数只有p,故1至p的整数只有p与p不互质
2. 如果i mod p = 0, 那么 phi(i * p)=phi(i) * p (我不会证明)
3.若i mod p ≠0, 那么 phi( i * p )=phi(i) * ( p-1 ) (我不会证明)
(所以我说我会证明都是骗人的╮( ̄▽ ̄)╭)
代码如下:
1 #include<cstdio> 2 using namespace std; 3 const int N = 1e6+10 ; 4 int phi[N], prime[N]; 5 int tot;//tot计数,表示prime[N]中有多少质数 6 void Euler(){ 7 phi[1] = 1; 8 for(int i = 2; i < N; i ++){ 9 if(!phi[i]){ 10 phi[i] = i-1; 11 prime[tot ++] = i; 12 } 13 for(int j = 0; j < tot && 1ll*i*prime[j] < N; j ++){ 14 if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-1); 15 else{ 16 phi[i * prime[j] ] = phi[i] * prime[j]; 17 break; 18 } 19 } 20 } 21 } 22 23 int main(){ 24 Euler(); 25 }
最后说下
a^b % p 不等价 (a%p)^(b%p) % p
因为
a^φ(p) ≡ 1 (mod p)
所以
a^b % p = (a%p)^(b%φ(p)) % p
(欧拉函数前提是a和p互质)
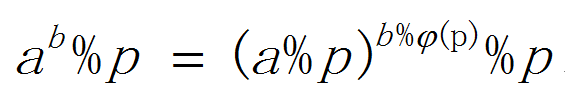
如果p是质数
直接用这个公式
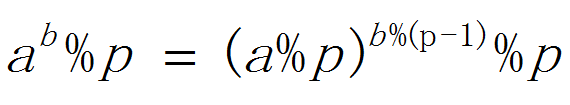
机智的代码,机智的我(。・`ω´・)
///////////////////////////////////////////////
2016年7月23号
我的天哪,我又发现了一个新公式,貌似可以摆脱a和p互质的束缚,让我们来命名为:超欧拉取模进化公式
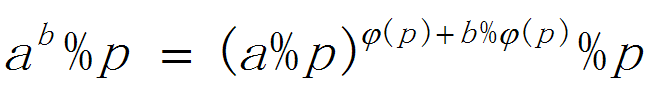
这是历史性的一刻,妈妈再也不用为a和p不互质而担心了= =


 浙公网安备 33010602011771号
浙公网安备 33010602011771号