图形学、02 推导证明 | 任意一点经过透视投影后 z 坐标相对于之前有什么变化

齐次坐标知识点： $\begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow\begin{bmatrix} nx \\ ny \\ nz \\ n \\\end{bmatrix}$ 两个都表示同一个点

透视投影：先将远截面按一定规则缩放到跟近截面一样大，然后再正交投影

缩放规则：远截面缩放后$z$不变，缩放过后大小同近截面相同。

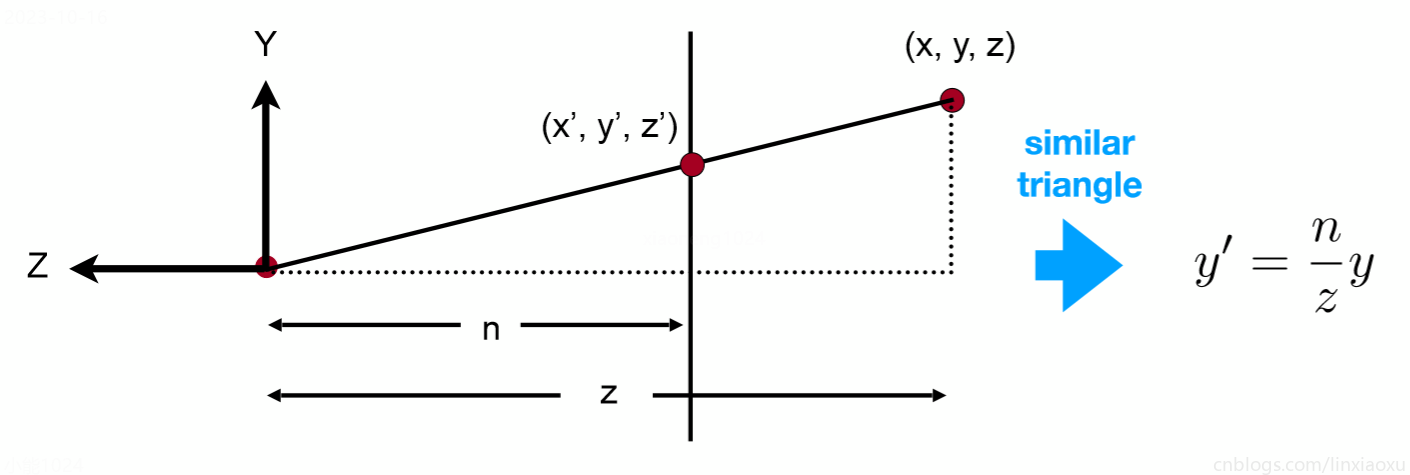
截取yz平面，$ZNear = n,ZFar = f$ ，则任意一点经过缩放后： $y^{’} = \frac{n}{z}y$ （相似三角形）

xz平面同理： $x^{’} = \frac{n}{z}x$ ，即 $\begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow\begin{bmatrix} \frac{n}{z}x \\ \frac{n}{z}y \\ unknown \\ 1 \\\end{bmatrix}\Rightarrow\begin{bmatrix}nx \\ ny \\ unknown \\ z \\\end{bmatrix}$

如此可以确定一部分矩阵参数：

$M_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ... & ... & ... & ... \\ 0 & 0 & 1 & 0 \\\end{bmatrix}$

对于近截面和远截面上的点，透视变换后z是不变的(缩放规则)

只看第三行的结果

$\begin{bmatrix} A&B&C&D\\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow z^2$

显然 $A = B = 0$ ，代入 $Z = n ，Z = f$ 有

$Cn+D = n^{2}$

$Cf+D = f^{2}$

得到 $C = n+f,D=-nf$

最后求得

$M_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\\end{bmatrix}$

课后问题：对于任意一个满足 $n\leq z\leq f$ 的点，经过透视投影后， z 坐标相对于之前有什么变化

$M_{persp\rightarrow ortho}\begin{bmatrix} x \\ y \\ z \\ 1 \\\end{bmatrix} \Rightarrow \begin{bmatrix} nx \\ ny \\ (n+f)z-nf \\ z\\\end{bmatrix}\Rightarrow \begin{bmatrix} \frac{n}{z}x \\ \frac{n}{z}y \\ \frac{(n+f)z-nf}{z} \\ 1\\\end{bmatrix}$

比较 $f(z) = \frac{(n+f)z-nf}{z} - z$ 跟0的关系即可，不妨乘以一个 z 得到：

$z*f(z) = -z^{2} + (n+f)z-nf = (z-n)(f-z)$

又 $n\leq z\leq f$ ，$z*f(z) \geq 0$ ，故 $f(z) \leq 0$，即透视投影后， z 坐标相对于以前离相机更远了

对 $f(z) = \frac{(n+f)z-nf}{z} - z$ ，对 $z$ 求偏导

$\begin{array}{l} \frac{\partial f}{\partial z}=\frac{(n+f) z-(n+f) z+nf}{z^{2}}-1 \\ \frac{\partial f}{\partial z}=\frac{n f}{z^{2}}-1=\frac{nf-z^{2}}{z^{2}} \\ z^{2}=nf \quad z= \pm \sqrt{nf} \end{array}$

从 $n$ 到 $- \sqrt{nf}$ 单调递增，从 $- \sqrt{nf}$ 到 $f$ 单调递减

分数怎么求导

$\begin{array}{l} g(x) \neq 0 , f(x) , g(x) \text { 均可导 } \\ {\left[\frac{f(x)}{g(x)}\right]^{\prime}=\frac{f^{\prime}(x) g(x)-g^{\prime}(x) f(x)}{[g(x)]^{2}}} \end{array}$