OpenCV入门(18):图像处理之边缘检测
在数字图像处理领域,边缘检测是一项至关重要的基础技术。它如同为图像赋予 “骨架”,帮助计算机快速识别图像中的物体轮廓、形状与结构,广泛应用于目标识别、图像分割、图像配准等多个领域。
边缘检测的核心目标是找出图像中像素灰度发生剧烈变化的区域边界。这些边界往往对应着图像中物体的轮廓、不同物体的交界处或纹理变化明显的地方。通过提取这些边缘信息,可以有效减少图像数据量,同时保留图像中最关键的结构特征,为后续的高级图像处理任务奠定基础。
OpenCV 中常用的边缘检测函数及其说明:
| 函数 | 算法 | 说明 | 适用场景 |
|---|---|---|---|
cv::Canny() |
Canny 边缘检测 | 多阶段算法,检测效果较好,噪声抑制能力强。 | 通用边缘检测,适合大多数场景。 |
cv::Sobel() |
Sobel 算子 | 基于一阶导数的边缘检测,可以检测水平和垂直边缘。 | 检测水平和垂直边缘。 |
cv::Scharr() |
Scharr 算子 | Sobel 算子的改进版本,对边缘的响应更强。 | 检测细微的边缘。 |
cv::Laplacian() |
Laplacian 算子 | 基于二阶导数的边缘检测,对噪声敏感。 | 检测边缘和角点。 |
一、什么是边缘?
1.1 边缘定义
在图像中,边缘可以看作是局部区域内像素灰度值的不连续性。从数学角度理解,灰度值的变化率在边缘处会出现显著变化。例如,在一幅黑白图像中,从黑色区域过渡到白色区域的边界处,像素灰度值会从较低值突然跃升至较高值,这个过渡区域就是边缘所在之处。
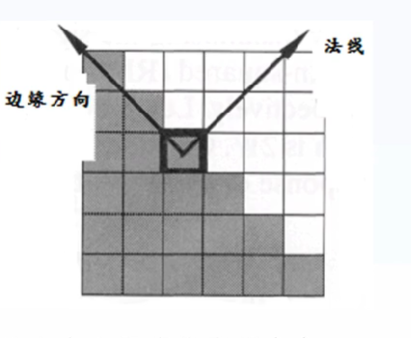
以图像像素值突变最大的方向作为边缘法线,与边缘法线垂直的就是边缘。
边缘强度:局部图像上的像素值突变程度(图像局部一阶梯度和二阶梯度值)。
1.2 边缘类型
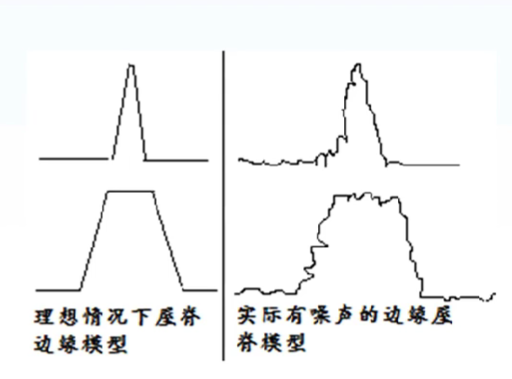
- 阶跃型边缘:像素灰度值在边缘两侧呈现明显的阶梯状变化,一侧灰度值较低,另一侧较高,中间过渡区域极窄,类似于一个理想的阶跃函数。
- 屋顶型边缘:灰度值从较低水平逐渐上升至峰值,然后又迅速下降到较低水平,边缘像素位于灰度值变化的峰值位置,形状类似屋顶。

1.3 梯度概念
为了准确检测出图像中的边缘,需要引入梯度的概念。在二维图像 f(x,y) 中,梯度是一个向量,它的方向指向图像灰度增长最快的方向,其幅值反映了灰度变化的剧烈程度。
1.4 边缘检测类型
边缘检测算子是利用图像边缘的突变性质来检测边缘的,通常情况下边缘检测有以下三种类型。
- 一阶微分:以一阶微分为基础的边缘检测,通过计算图像的梯度值来检测图像边缘,如 Sobel 算子,Prewitt 算子,Roberts 算子及差分边缘检测。
- 二阶微分:以二阶微分为基础的边缘检测,通过寻求二阶导数中的过零点来检测边缘,如拉普拉斯算子,高拉普拉斯算子,Canny 算子边缘检测。
- 混合一阶微分和二阶微分:以混合一阶微分和二阶微分为基础的边缘检测,综合利用一阶微分和二阶微分的特征,如 Marr-Hildreth 边缘检测算子。
二、Canny 边缘检测
Canny 边缘检测是一种多阶段的边缘检测算法,由 John F. Canny 在 1986 年提出。Canny 边缘检测被认为是边缘检测的"金标准",因为它能够在噪声抑制和边缘定位之间取得良好的平衡。
Canny 边缘检测算子是传统边缘检测算子中最优秀的,Canny 检测基于下面三个目标:
- 低错误率。即所有边缘都应该找到,并且没有虚假边缘。
- 准确的定位边缘。即检测到的边缘应该接近真实的边缘。
- 单个边缘点响应。即对于边缘检测,只返回单点厚度的结果。
2.1 Canny 边缘检测的步骤
Canny 边缘检测算法主要包括以下几个步骤:
(1)噪声抑制:使用高斯滤波器对图像进行平滑处理,以减少噪声的影响。
(2)计算梯度:使用 Sobel 算子计算图像的梯度幅值和方向。
(3)非极大值抑制:沿着梯度方向,保留局部梯度最大的像素点,抑制其他像素点。
(4)双阈值检测:使用两个阈值(低阈值和高阈值)来确定真正的边缘。高于高阈值的像素点被认为是强边缘,低于低阈值的像素点被抑制,介于两者之间的像素点如果与强边缘相连则保留。
(5)边缘连接:通过滞后阈值处理,将弱边缘与强边缘连接起来,形成完整的边缘。
2.2 API
在 OpenCV 中,可以使用 cv::Canny() 函数来实现 Canny 边缘检测。该函数的原型如下:
void Canny( InputArray image, OutputArray edges,
double threshold1, double threshold2,
int apertureSize = 3, bool L2gradient = false );
image:输入图像,必须是单通道的灰度图像。edges:输出的边缘图像,为单通道黑白图。threshold1:低阈值。threshold2:高阈值。apertureSize:Sobel 算子的孔径大小,默认为 3。L2gradient:是否使用 L2 范数计算梯度幅值,默认为 False(使用 L1 范数)。
2.3 示例代码
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main() {
// 读取图像
Mat img1 = imread("lena.jpg", 0); // 读取灰度图像
if (img1.empty())
{
cout << "读取错误" << endl;
return -1;
}
imshow("img1", img1);
// 定义输出的边缘图像,为单通道黑白图
Mat img2 = Mat(img1.size(), CV_8U, Scalar(0));
// OpenCV自带canny检测函数
Canny(img1, img2, 50, 150);
imshow("img2", img2);
waitKey(0);
return 0;
}
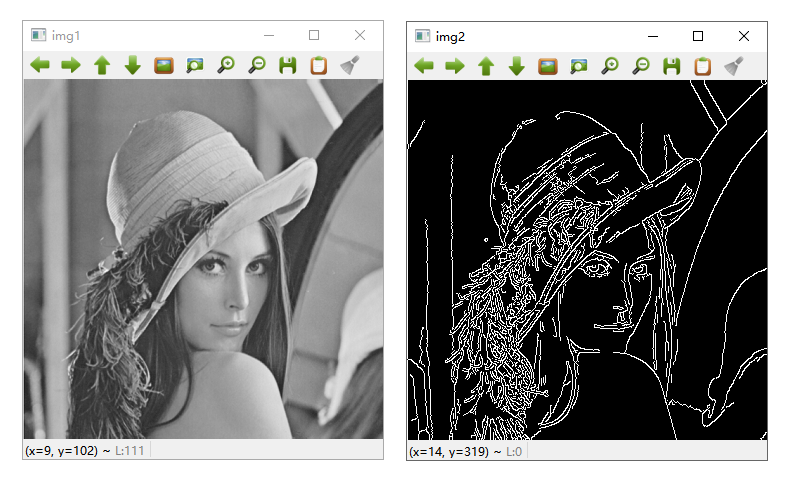
效果图如下所示:
三、Sobel 算子
Sobel 算子是一种基于梯度的边缘检测算子,它通过计算图像在水平和垂直方向上的梯度来检测边缘。Sobel 算子结合了高斯平滑和微分操作,因此对噪声具有一定的抑制作用。
3.1 Sobel 算子的原理
Sobel 算子使用两个 3x3 的卷积核分别计算图像在水平和垂直方向上的梯度:
-
水平方向的卷积核:
[-1, 0, 1] [-2, 0, 2] [-1, 0, 1] -
垂直方向的卷积核:
[-1, -2, -1] [ 0, 0, 0] [ 1, 2, 1]
通过这两个卷积核,可以分别得到图像在水平和垂直方向上的梯度 Gx 和 Gy。最终的梯度幅值可以通过以下公式计算:
G = sqrt(Gx^2 + Gy^2)
3.2 API
在 OpenCV 中,可以使用 cv::Sobel() 函数来计算图像的梯度。该函数的原型如下:
void Sobel( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, int ksize = 3,
double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
src:输入图像。ddepth:输出图像的深度,通常使用cv2.CV_64F。dx:x 方向上的导数阶数。dy:y 方向上的导数阶数。ksize:Sobel 核的大小,默认为 3。scale:缩放因子,默认为 1。delta:可选的 delta 值,默认为 0。borderType:边界填充类型,默认为cv2.BORDER_DEFAULT。
3.3 示例代码
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main() {
// 读取图像
Mat image = imread("lena.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cout << "Could not open or find the image" << endl;
return -1;
}
// Sobel算子检测
Mat sobelX, sobelY;
Sobel(image, sobelX, CV_16S, 1, 0, 3);
Sobel(image, sobelY, CV_16S, 0, 1, 3);
// 转换为绝对值
Mat sobelXAbs, sobelYAbs;
convertScaleAbs(sobelX, sobelXAbs);
convertScaleAbs(sobelY, sobelYAbs);
// 获取整幅图的一阶边缘
Mat edges;
//edges = sobelXAbs + sobelYAbs; // 使用这句也可以代替addWeighted
addWeighted(sobelXAbs, 0.5, sobelYAbs, 0.5, 0, edges);
imshow("Original Image", image);
imshow("Sobel Edge Detection", edges);
waitKey(0);
return 0;
}
Sobel 函数参数说明:
image:输入图像。gradient_x/gradient_y:输出的梯度图像,CV_16S表示输出图像的数据类型为 16 位有符号整数,这是为了防止在计算梯度过程中出现溢出。1, 0或0, 1:分别表示在x方向或y方向上计算梯度,若为1则表示该方向上进行求导,0表示不求导。3:表示 Sobel 算子的孔径大小,即卷积核大小为 3×3。
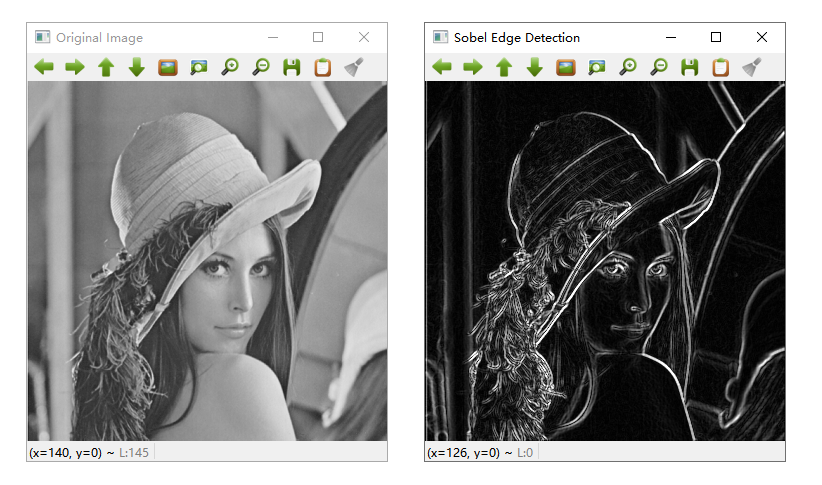
效果图如下所示:
四、Scharr 算子
Scharr 算子是 Sobel 算子的改进版本,两者主要是 X 和 Y 方向的滤波器(卷积核)不同。Scharr 算子可以看成 Sobel 算子的加强版,对一些导数较小(即像素值差距不大)的弱边缘仍然可以检测出。
4.1 API
在 OpenCV 中,可以使用 cv::Scharr() 函数来计算图像的 Scharr 值。
该函数的原型如下:
void Scharr( InputArray src, OutputArray dst, int ddepth,
int dx, int dy, double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
跟 Sobel 函数的参数一致,这里不再赘述。
4.3 示例代码
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main() {
// 读取图像
Mat image = imread("lena.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cout << "Could not open or find the image" << endl;
return -1;
}
// Scharr算子检测
Mat scharrX, scharrY;
Scharr(image, scharrX, CV_16S, 1, 0);
Scharr(image, scharrY, CV_16S, 0, 1);
// 转换为绝对值
Mat scharrXAbs, scharrYAbs;
convertScaleAbs(scharrX, scharrXAbs);
convertScaleAbs(scharrY, scharrYAbs);
// 整幅图的一阶边缘
Mat edges;
//edges = scharrXAbs + scharrYAbs; // 使用这句也可以代替addWeighted
addWeighted(scharrXAbs, 0.5, scharrYAbs, 0.5, 0, edges);
imshow("Original Image", image);
imshow("Sobel Edge Detection", edges);
waitKey(0);
return 0;
}
从结果可以看出,Scharr 算子会检测出更多的边缘。效果图如下所示:
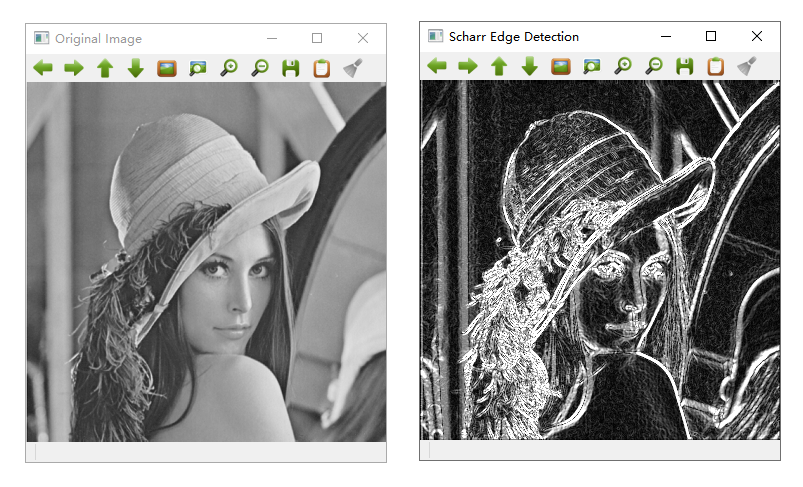
五、Laplacian 算子
Laplacian 算子是一种二阶微分算子,它通过计算图像的二阶导数来检测边缘。Laplacian 算子对噪声比较敏感,因此通常在使用之前会对图像进行高斯平滑处理。
5.1 Laplacian 算子的原理
Laplacian 算子使用以下卷积核来计算图像的二阶导数:
[ 0, 1, 0]
[ 1, -4, 1]
[ 0, 1, 0]
通过这个卷积核,可以得到图像的 Laplacian 值。Laplacian 值较大的区域通常对应于图像的边缘。
5.2 API
在 OpenCV 中,可以使用 cv::Laplacian() 函数来计算图像的 Laplacian 值。
该函数的原型如下:
void Laplacian( InputArray src, OutputArray dst, int ddepth,
int ksize = 1, double scale = 1, double delta = 0,
int borderType = BORDER_DEFAULT );
src:输入图像。ddepth:输出图像的深度,通常使用cv::CV_64F。ksize:Laplacian 核的大小,默认为 1。scale:缩放因子,默认为 1。delta:可选的 delta 值,默认为 0。borderType:边界填充类型,默认为cv::BORDER_DEFAULT。
5.3 示例代码
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main() {
// 读取图像
Mat image = imread("lena.jpg", IMREAD_GRAYSCALE);
if (image.empty()) {
cout << "Could not open or find the image" << endl;
return -1;
}
cv::Mat edges1, edges2, Gresult;
// Laplacian算子检测(未滤波的)
cv::Laplacian(image, edges1, CV_16S, 3, 1, 0);
// 转换为绝对值
cv::convertScaleAbs(edges1, edges1);
// Laplacian算子检测(进行高斯滤波的)
cv::GaussianBlur(image, Gresult, cv::Size(3, 3), 5, 0); // 进行高斯滤波
cv::Laplacian(Gresult, edges2, CV_16S, 3, 1, 0);
cv::convertScaleAbs(edges2, edges2);
imshow("Original Image", image);
imshow("Laplacian Edge Detection ", edges1);
imshow("Laplacian Edge Detection GaussianBlur", edges2);
waitKey(0);
return 0;
}
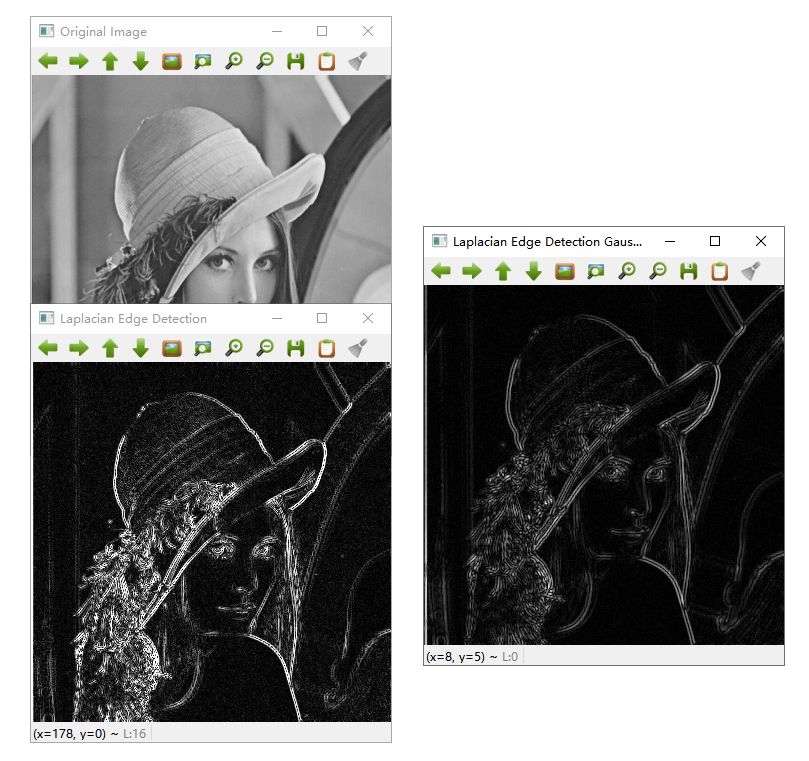
效果图如下所示:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号