OpenCV入门(12):基本操作之像素归一化
一、什么是归一化?
概念一:归一化是把需要处理的数据通过某种算法处理后限制在所需要的一定范围内。
概念二:归一化是指在处理数据的过程中,把数据范围相差较大的数据进行标准化处理,让所有的数据都处于同一个数量级中。
二、为什么要归一化?
首先,归一化是 为了后面数据处理的方便,其次是保证程序运行时收敛加快。归一化的具体作用是归纳统一样本的统计分布性。归一化在 0-1 之间是统计的概率分布,归一化在某个区间上是统计的坐标分布。
归一化的目的,是使得没有可比性的数据变得具有可比性,同时又保持相比较的两个数据之间的相对关系,如大小关系;或是为了作图,原来很难在一张图上作出来,归一化后就可以很方便的给出图上的相对位置等。
三、归一化的方法
cv::normalize 归一化数据。该函数分为范围归一化与数据值归一化。
void cv::normalize ( InputArray src, // 输入数组;
InputOutputArray dst, // 输出数组,数组的大小和原数组一致;
double alpha = 1, // 1,用来规范值,2.规范范围,并且是下限;
double beta = 0, // beta=0,则alpha = 1,规范值;beta不为0,只用来规范范围并且是上限;
int norm_type = NORM_L2, // 归一化选择的数学公式类型;
int dtype = -1, // 当为负,输出在大小深度通道数都等于输入,当为正,输出只在深度与输入不同,不同的地方由dtype决定;
InputArray mask = noArray() ) // 掩码。选择感兴趣区域,选定后只能对该区域进行操作。
归一化选择的数学公式类型:
NORM_MINMAX: 数组的数值被平移或缩放到一个指定的范围,线性归一化。NORM_INF: 归一化数组的(切比雪夫距离)L∞范数(绝对值的最大值)NORM_L1: 归一化数组的(曼哈顿距离)L1-范数(绝对值的和)NORM_L2: 归一化数组的(欧几里德距离)L2-范数
关于 norm_type 归一化选择的数学公式图如下:
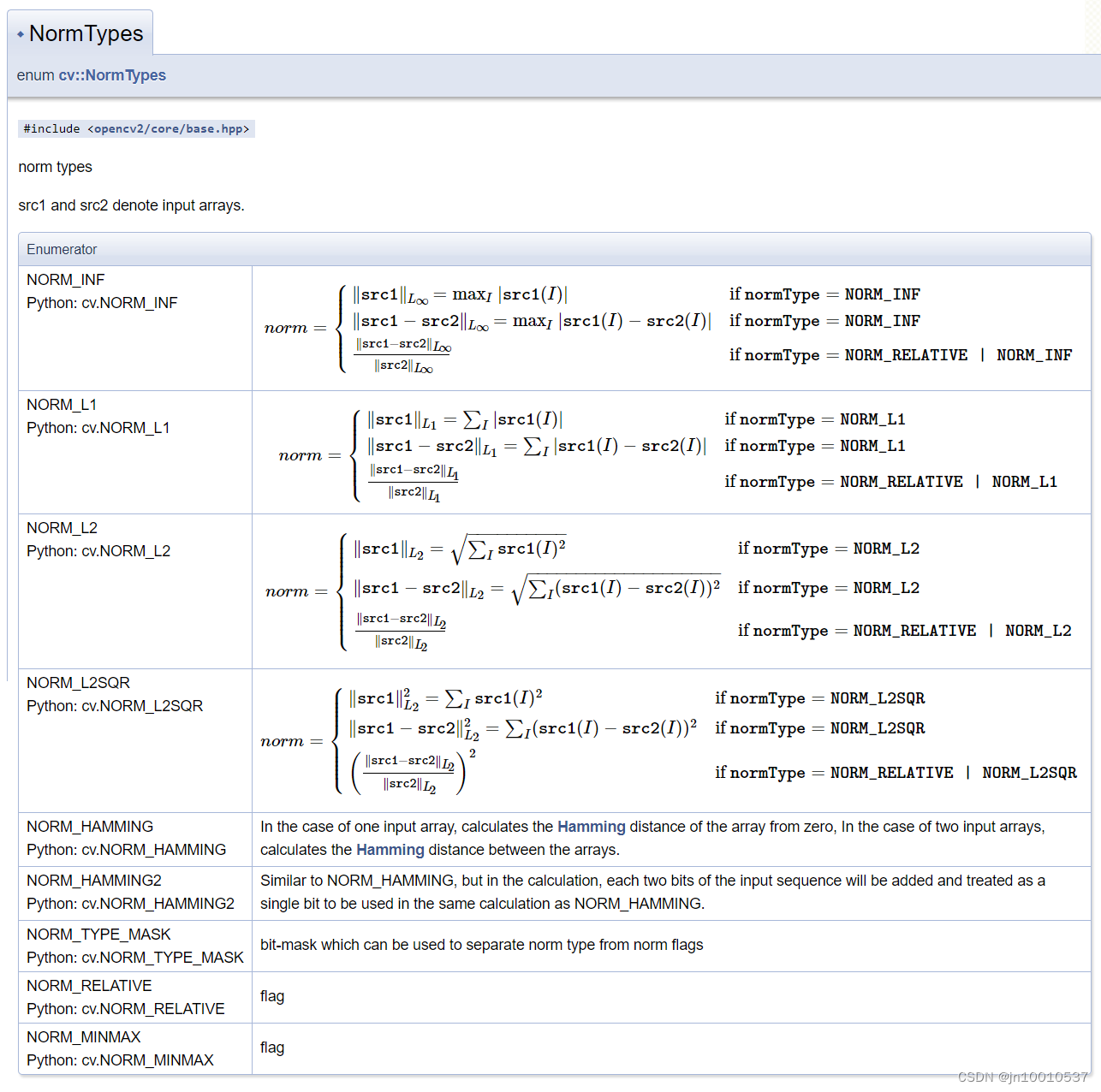
举例说明:
src={10, 23, 71}
NORM_L1 运算后得到: dst={0.096, 0.221, 0.683}
NORM_INF 运算后得到: dst={0.141, 0.324, 1}
NORM_L2 运算后得到: dst={0.133, 0.307, 0.947}
NORM_MINMAX 运算得到: dst={0, 0.377, 1}
四、示例
4.1 示例:值归一化
以下是值归一化:
#include<opencv2/opencv.hpp>
#include<iostream>
using namespace std;
int main(){
std::vector<double> src1 = { 5,3,7,10 };
std::vector<double> src2, src3, src4, src5;
cv::normalize(src1, src2, 1, 0, cv::NORM_L1); // beta=0,用来规范值
cv::normalize(src1, src3, 1, 0, cv::NORM_L2); // beta=0,用来规范值
cv::normalize(src1, src4, 1, 0, cv::NORM_INF); // beta=0,用来规范值
cv::normalize(src1, src5, 1, 0, cv::NORM_MINMAX); // beta=0,用来规范值
std::cout << "[INFO] src: { 5, 3, 7, 10 }" << std::endl;
std::cout << "[INFO] NORM_L1: ";
for (int i = 0; i < src2.size(); i++){
std::cout << src2[i] << "; ";
}
std::cout << std::endl;
std::cout << "[INFO] NORM_L2: ";
for (int i = 0; i < src3.size(); i++) {
std::cout << src3[i] << "; ";
}
std::cout << std::endl;
std::cout << "[INFO] :NORM_INF: ";
for (int i = 0; i < src4.size(); i++) {
std::cout << src4[i] << "; ";
}
std::cout << std::endl;
std::cout << "[INFO] :NORM_MINMAX: ";
for (int i = 0; i < src5.size(); i++) {
std::cout << src5[i] << "; ";
}
std::cout << std::endl;
return 0;
}
运行结果如下:
[INFO] src: { 5, 3, 7, 10 }
[INFO] NORM_L1: 0.2; 0.12; 0.28; 0.4;
[INFO] NORM_L2: 0.369611; 0.221766; 0.517455; 0.739221;
[INFO] :NORM_INF: 0.5; 0.3; 0.7; 1;
[INFO] :NORM_MINMAX: 0.285714; 0; 0.571429; 1;
4.2 示例:范围归一化
以下是范围归一化:
#include<opencv2/opencv.hpp>
#include<iostream>
using namespace std;
int main(){
std::vector<double> src1 = { 5,3,7,10 };
std::vector<double> src2, src3, src4, src5;
cv::normalize(src1, src2, 1, 255, cv::NORM_L1); // beta不为0,,使用范围归一化
cv::normalize(src1, src3, 1, 255, cv::NORM_L2); // beta不为0,,使用范围归一化
cv::normalize(src1, src4, 0, 255, cv::NORM_INF); // beta不为0,,使用范围归一化
cv::normalize(src1, src5, 0, 255, cv::NORM_MINMAX); // beta不为0,,使用范围归一化
std::cout << "[INFO] src: { 5, 3, 7, 10 }" << std::endl;
std::cout << "[INFO] NORM_L1: ";
for (int i = 0; i < src2.size(); i++){
std::cout << src2[i] << "; ";
}
std::cout << std::endl;
std::cout << "[INFO] NORM_L2: ";
for (int i = 0; i < src3.size(); i++) {
std::cout << src3[i] << "; ";
}
std::cout << std::endl;
std::cout << "[INFO] :NORM_INF: ";
for (int i = 0; i < src4.size(); i++) {
std::cout << src4[i] << "; ";
}
std::cout << std::endl;
std::cout << "[INFO] :NORM_MINMAX: ";
for (int i = 0; i < src5.size(); i++) {
std::cout << src5[i] << "; ";
}
std::cout << std::endl;
return 0;
}
运行结果如下:
[INFO] src: { 5, 3, 7, 10 }
[INFO] NORM_L1: 0.2; 0.12; 0.28; 0.4;
[INFO] NORM_L2: 0.369611; 0.221766; 0.517455; 0.739221;
[INFO] :NORM_INF: 0; 0; 0; 0;
[INFO] :NORM_MINMAX: 72.8571; -7.10543e-015; 145.714; 255;
4.3 示例:图像示例
//流程:
//读取图片--》判断并显示图片--》转换为灰度图--》转换为浮点数类型数组--》四种归一化方式
//1)scale and shift by NORM_MINMAX
//2)scale and shift by NORM_INF
//3)scale and shift by NORM_L1
//4)scale and shift by NORM_L2
//--》归一化的范围设置为1.0 - 0
//--》不同的归一化方式结果出来要乘以对应的数值
//--》将结果转换为CV_8UC1
//--》显示图片
#include"opencv2\opencv.hpp"
#include"iostream"
using namespace std;
using namespace cv;
int main(int argc, char** argv)
{
Mat src = imread("leaf.jpg");
if (src.empty())
{
printf("Could not load image...\n");
return -1;
}
imshow("srcImg", src);
Mat src_gray, src_gray_f;
cvtColor(src, src_gray, COLOR_RGB2GRAY);//转换为灰度图
src_gray.convertTo(src_gray_f, CV_32F);//转换为浮点数类型数组
//scale and shift by NORM_MINMAX
Mat dst = Mat::zeros(src_gray.size(), CV_32FC1);
normalize(src_gray_f, dst, 1.0, 0, NORM_MINMAX);
Mat result = dst * 255;
result.convertTo(dst, CV_8UC1);
imshow("NORM_MINMAX", dst);
//scale and shift by NORM_INF
normalize(src_gray_f, dst, 1.0, 0, NORM_INF);
result = dst * 255;
result.convertTo(dst, CV_8UC1);
imshow("NORM_INF", dst);
//scale and shift by NORM_L1
normalize(src_gray_f, dst, 1.0, 0, NORM_L1);
result = dst * 100000000;
result.convertTo(dst, CV_8UC1);
imshow("NORM_L1", dst);
//scale and shift by NORM_L2
normalize(src_gray_f, dst, 1.0, 0, NORM_L2);
result = dst * 10000;
result.convertTo(dst, CV_8UC1);
imshow("NORM_L2", dst);
waitKey(0);
return 0;
}
效果图如下所示:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号