浅谈李超线段树
浅谈李超线段树
概论
要求在平面直角坐标系下维护两个操作:
- 在平面上加入一条线段。
- 给定一个数 \(k\),询问与直线 \(x = k\) 相交的线段的交点的纵坐标最值。
李超线段树就是能够维护以上两个操作的数据结构。
基本概念
首先需要明确:李超树是一种线段树,它的一个节点存储的是一个区间 \([l,r]\) 上值最大的线段的编号的懒标记。
为什么说是懒标记?就是指这条线段并不一定最大(小),而是可能取到最值。
这就需要谈到,李超线段树是一种基于标记永久化的线段树。
标记永久化就是指修改时一路更改被影响到的节点,询问时则一路累加路上的标记,从而省去标记上传下传的操作。
也就是说,我们不保证存储 \([l,r]\) 的节点的编号一定在整个区间上取到最值,但保证对于任意 \(x=p\) ,结合所有包含 \(p\) 的区间 \([l,r]\) 取最值一定可以取到 \(p\) 的最值。
举个例子,假设现在横坐标范围是 \([1,4]\),对于 \(x=2\),我们需要保证区间 \([1,4]\)、\([1,2]\),\([2,2]\) 中存储的线段编号至少有一个在 \(x=2\) 可以取到最值,也就是说取这三个区间的最值就是这个点的最值。
以上就是标记永久化的思想,可以方便修改,也不会使查询复杂度升高。
插入直线
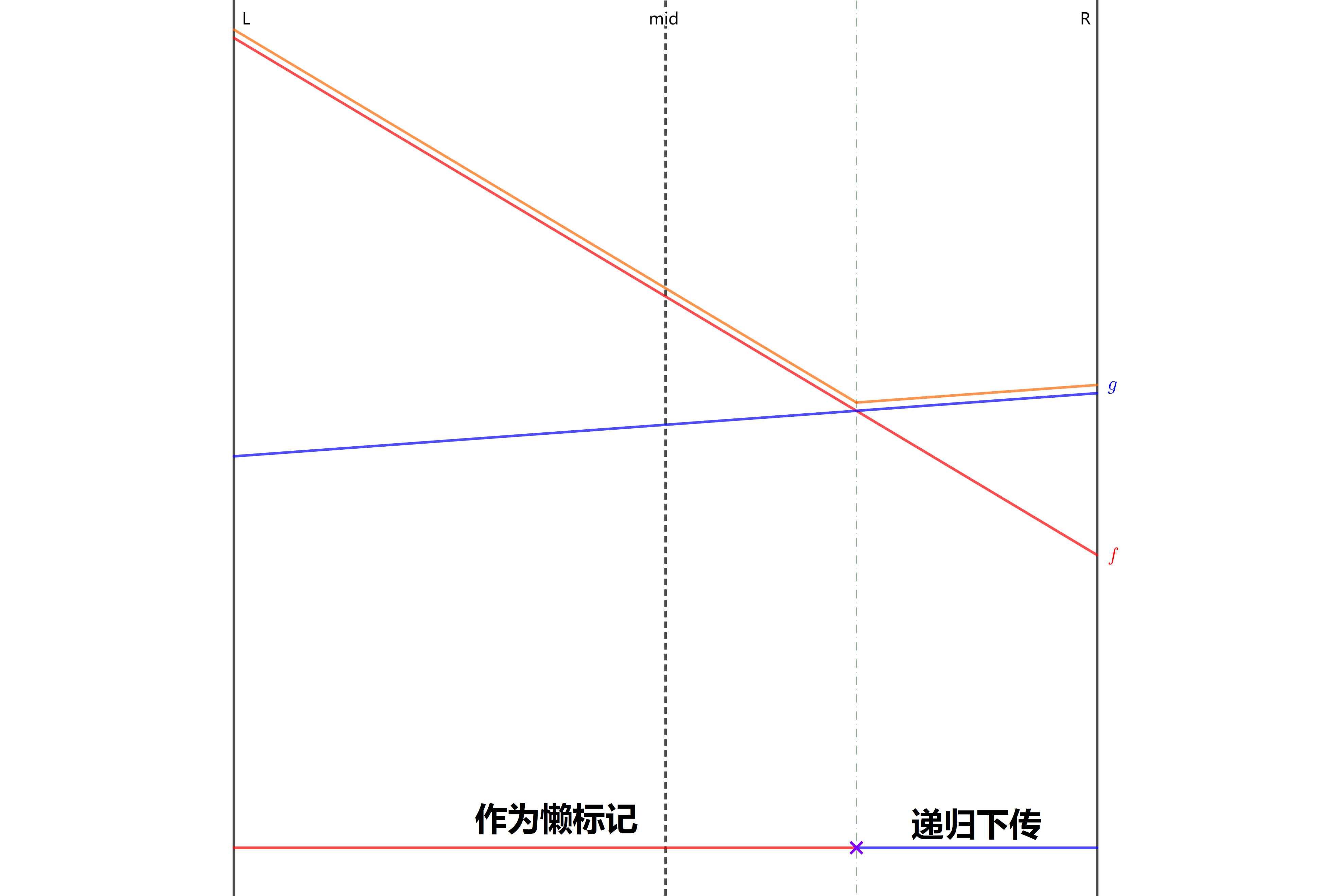
我们先来考虑插入直线,即覆盖整个区间的线,下面默认取最大值,最小值同理。
分类讨论,对于每一个区间 \([l,r]\):
- 若区间 \([l,r]\) 没有直线覆盖,直接将标记改为这条直线的编号然后返回即可。
- 若区间 \([l,r]\) 有直线覆盖,考虑此区间的懒标记所表示的直线 \(f\) 和插入的直线 \(g\),不妨令原来的懒标记直线 \(f\) 在中点 \(mid\) 处取值大,即 \(f(mid)\ge g(mid)\)(代码上,如果插入线段在中点处取值大就和懒标记
swap即可)。- 如果 \(f(l)\ge g(l)\) 则在左区间 \([l,mid]\) 上 \(f\) 一定不比 \(g\) 劣,也就是说 \(g\) 对左区间最值不可能有影响,不需要再递归处理左区间,右区间同理。
- 如果 \(f(l)<g(l)\) 则在左区间 \([l,mid]\) 上 \(f\) 可能比 \(g\) 劣,由于 \(f\) 不一定就是这段区间的最值,那么我们递归左区间下传标记 \(g\),右区间同理。
我们可以发现,如果这么做,对于每一个 \(x=p\),结合所有包含这个点的区间,一定能取到最值。
因为对于每一条插入的线段,如果它在当前区间中点的取值大,那么原来的标记就会被替换,这也就使在这条线段上取到最值的点都被覆盖,又为了保证不影响在原线段取到最值的点,又下传原线段,使在原线段取到最值的点都被原线段覆盖,这样就满足的标记永久化的要求。
时间复杂度;\(O(\log n)\)。
代码(\(p\) 存储直线,\(dat\) 是懒标记):
struct line
{
double k, b;
int id;
inline double calc(int x)
{
return k * x + b;
}
} p[N];
void update(int x, int l, int r, int k)
{
if (!dat[x])
{
dat[x] = k;
return;
}
if (p[k].calc(mid) - p[dat[x]].calc(mid) > eps)
{
swap(k, dat[x]);
}
if (p[k].calc(l) - p[dat[x]].calc(l) > eps)
{
update(ls, l, mid, k);
}
if (p[k].calc(r) - p[dat[x]].calc(r) > eps)
{
update(rs, mid + 1, r, k);
}
}
插入线段
与插入直线不同的是,插入线段有定义域的限制。
与普通线段树一样,我们可以把要插入的区间分成至多 \(\log n\) 个在线段树上的区间,然后对每一个被插入区间包含的区间像插入直线一样下传标记即可。
线段树区间操作的本质就是将一个区间分成至多 \(\log n\) 个在线段树上的区间
—— KevinLikesCoding 大神
代码:
void update(int x, int l, int r, int ql, int qr, int k)
{
if (r < ql || l > qr)
{
return;
}
if (ql <= l && r <= qr)
{
if (!dat[x])
{
dat[x] = k;
return;
}
if (p[k].calc(mid) - p[dat[x]].calc(mid) > eps)
{
swap(k, dat[x]);
}
if (p[k].calc(l) - p[dat[x]].calc(l) > eps)
{
update(ls, l, mid, ql, qr, k);
}
if (p[k].calc(r) - p[dat[x]].calc(r) > eps)
{
update(rs, mid + 1, r, ql, qr, k);
}
return;
}
update(ls, l, mid, ql, qr, k);
update(rs, mid + 1, r, ql, qr, k);
}
查询最值
根据标记永久化的性质,我们只需递归遍历所有包含这个点的区间再取最大值即可。
代码(需要说明的是,我这里建了一个虚拟线段 \(0\),如果 dat[x]==0,\(res\) 就会被赋值为虚拟线段在 \(k\) 处的值,最大值就赋值为负无限,最小值赋值为正无限即可):
double query(int x, int l, int r, int k)
{
if (r < k || l > k)
{
return INT_MIN;
}
double res = p[dat[x]].calc(k);
if (l == r)
{
return res;
}
return max(res, max(query(ls, l, mid, k), query(rs, mid + 1, r, k)));
}
例题
【模板】李超线段树 / [HEOI2013] Segment
题目描述
要求在平面直角坐标系下维护两个操作:
- 在平面上加入一条线段。记第 \(i\) 条被插入的线段的标号为 \(i\)。
- 给定一个数 \(k\),询问与直线 \(x = k\) 相交的线段中,交点纵坐标最大的线段的编号。
本题输入强制在线。
数据范围
对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 10^5\),\(1 \leq k, x_0, x_1 \leq 39989\),\(1 \leq y_0, y_1 \leq 10^9\)。
解题思路
李超线段树板子,上面已经讲的很清楚了。
代码
#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 1e5 + 10, P1 = 39989, P2 = 1e9;
const double eps = 1e-10;
int n, cnt, lst;
struct line
{
double k, b;
int id;
inline double calc(int x)
{
return k * x + b;
}
inline void ins(int x0, int y0, int x1, int y1)
{
if (x0 == x1)
{
k = 0, b = max(y1, y0);
return;
}
k = 1.0 * (y1 - y0) / (x1 - x0);
b = 1.0 * y0 - k * x0;
}
} p[N];
struct SGT
{
#define ls x << 1
#define rs x << 1 | 1
#define mid ((l + r) >> 1)
int dat[N << 2];
inline pair<double, int> mx(pair<double, int> a, pair<double, int> b)
{
if (a.first - b.first > eps)
{
return a;
}
else if (b.first - a.first > eps)
{
return b;
}
else
{
return a.second < b.second ? a : b;
}
}
void update(int x, int l, int r, int ql, int qr, int k)
{
if (r < ql || l > qr)
{
return;
}
if (ql <= l && r <= qr)
{
if (!dat[x])
{
dat[x] = k;
return;
}
if (p[k].calc(mid) - p[dat[x]].calc(mid) > eps)
{
swap(k, dat[x]);
}
if (p[k].calc(l) - p[dat[x]].calc(l) > eps || (p[k].calc(l) == p[dat[x]].calc(l) && k < dat[x]))
{
update(ls, l, mid, ql, qr, k);
}
if (p[k].calc(r) - p[dat[x]].calc(r) > eps || (p[k].calc(r) == p[dat[x]].calc(r) && k < dat[x]))
{
update(rs, mid + 1, r, ql, qr, k);
}
return;
}
update(ls, l, mid, ql, qr, k);
update(rs, mid + 1, r, ql, qr, k);
}
pair<double, int> query(int x, int l, int r, int k)
{
if (r < k || l > k)
{
return make_pair(0, 0);
}
pair<double, int> res = make_pair(p[dat[x]].calc(k), dat[x]);
if (l == r)
{
return res;
}
return mx(res, mx(query(ls, l, mid, k), query(rs, mid + 1, r, k)));
}
} t;
int main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
while (n--)
{
int op;
cin >> op;
if (op == 0)
{
int k;
cin >> k;
k = (k + lst - 1) % P1 + 1;
cout << (lst = t.query(1, 1, P1, k).second) << endl;
}
else
{
int x0, y0, x1, y1;
cin >> x0 >> y0 >> x1 >> y1;
x0 = (x0 + lst - 1) % P1 + 1;
y0 = (y0 + lst - 1) % P2 + 1;
x1 = (x1 + lst - 1) % P1 + 1;
y1 = (y1 + lst - 1) % P2 + 1;
p[++cnt].ins(x0, y0, x1, y1);
t.update(1, 1, P1, min(x0, x1), max(x0, x1), cnt);
}
}
return 0;
}
结语
恭喜你学会了李超线段树!
可以看到,我给出的李超线段树的例题只有一道板子,这是因为单独应用李超线段树的题目很少,李超线段树大多都和斜率化一起使用。
有关斜率优化的内容,我在 浅谈斜率优化 中都有讲到,欢迎继续学习!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号