快速幂求组合数

根据公式直接计算：

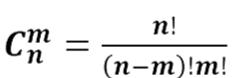
因为有除法取模，所以要逆元，要预处理求阶乘，和阶乘相对应的模逆元
阶乘很好求，阶乘逆元先算n!的逆元，然后再逆推回去，时间复杂度O（n）

#include <iostream>
#include <vector>
#define ll long long
using namespace std;
const int MOD = 1e9 + 7;
const int MAX_N = 100000;
ll quick_pow(ll base, ll exp, ll mod) {
	ll result = 1;
	base %= mod;
	while (exp > 0) {
		if (exp % 2 == 1) {
			result = (result * base) % mod;
		}
		base = (base * base) % mod;
		exp /= 2;
	}
	return result;
}
ll combination(int n, int k) {
	if (k < 0 || k > n) return 0;
	if (k == 0 || k == n) return 1;
	vector<ll> f(n + 1, 1);
	vector<ll> g(n + 1, 1);
	for (int i = 1; i <= n; ++i) {
		f[i] = (f[i - 1] * i) % MOD;
	}
	g[n] = quick_pow(f[n], MOD - 2, MOD);
	for (int i = n - 1; i >= 0; --i) {
		g[i] = (g[i + 1] * (i + 1)) % MOD;
	}
	return (f[n] * g[k] % MOD) * g[n - k] % MOD;
}

int main() {
	int n, k;
	cin >> n >> k;
	ll result = combination(n, k);
	return 0;
}