方法和前面的求约数个数类似
首先明确约数和定理
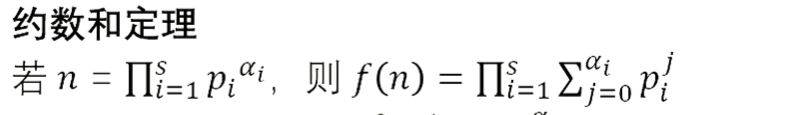
image

然后分为两种情况，一种是i能被p[i]整除，一种是不能，然后注意这里的区别，如果能被整除，那么i包含m的所有质因数且p[j]为m的最小质因数，且m只在p[j]的次数上比i多了一次
然后根据这个来进行各种判断

using namespace std;

const int N = 1000010;
int p[N], vis[N], cnt;
//g[i]表示i的最小质因子的1+p^1+...+p^k
int g[N], f[N];//f[i]表示i的约数和

void get_f(int n){ //筛法求约数和
  g[1] = f[1] = 1;
  for(int i=2; i<=n; i++){
    if(!vis[i]){
      p[++cnt] = i;
      g[i] = f[i] = i+1;
    }
    for(int j=1; i*p[j]<=n; j++){
      int m = i*p[j]; 
      vis[m] = 1;
      if(i%p[j] == 0){
        g[m] = g[i]*p[j]+1;
        f[m] = f[i]/g[i]*g[m];
        break;
      } 
      else{
        g[m] = p[j]+1;
        f[m] = f[i]*g[m];
      }
    }
  }
}
int main(){
  int n;
  cin >> n;
  get_f(n);
  for(int i=1; i<=n; i++)
    printf("%d\n",f[i]);
  return 0;
}

image