曼哈顿距离:dis=|xi-xj|+|yi-yj|要求最大最小的曼哈顿距离可以分别求横坐标和纵坐标的最大最小值,曼哈顿距离坐标相互独立
切比雪夫距离:dis=max(|ui-uj|,|vi-vj|)要求最大最小的距离直接看所有切比雪夫坐标下,u,v的最大最小值,就是挑出u的最大值和v的最大值,然后再从这两个数里选最大值,就是所有数据的最大值。
曼哈顿坐标->切比雪夫坐标:(x,y)->(x+y,x-y) 即u=x+y,v=x-y。
如:杭电2025春季联赛第三场1010:

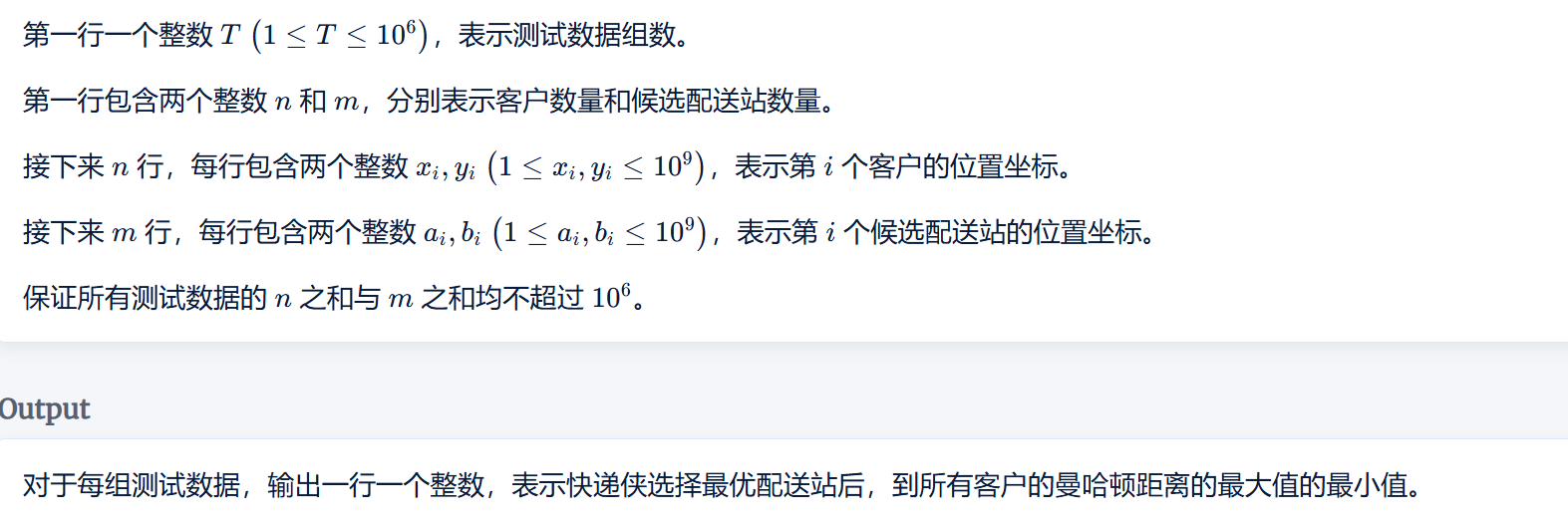
先放代码:
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int T;
cin >> T;
while (T--) {
int n, m;
cin >> n >> m;
// 预处理客户的u=x+y和v=x-y,计算极值
long long u_min = LLONG_MAX, u_max = LLONG_MIN;
long long v_min = LLONG_MAX, v_max = LLONG_MIN;
for (int i = 0; i < n; ++i) {
long long x, y;
cin >> x >> y;
long long u = x + y;
long long v = x - y;
u_min = min(u_min, u);
u_max = max(u_max, u);
v_min = min(v_min, v);
v_max = max(v_max, v);
}
// 遍历所有配送站,找最小的最大距离
long long ans = LLONG_MAX;
for (int i = 0; i < m; ++i) {
long long a, b;
cin >> a >> b;
long long s = a + b;
long long t = a - b;
// 计算max(|u_i - s|)
long long max_u = max(s - u_min, u_max - s);
// 计算max(|v_i - t|)
long long max_v = max(t - v_min, v_max - t);
// 当前配送站的最大距离
long long current = max(max_u, max_v);
ans = min(ans, current);
}
cout << ans << '\n';
}
return 0;
}`
先将坐标转换成切比雪夫坐标,因为最大曼哈顿距离就等于切比雪夫坐标下最大横纵坐标,但是要比较每一个点,所以先找到最大最小的u和v的坐标。
这样的话在后面遍历配送站坐标就可以直接去和之前求到的最大最小值计算就行。

