BUAA OO 第一单元总结
BUAA OO 第一单元总结
〇.综述
第一单元以解析、展开、合并表达式为背景,渗透了许多面向对象的基本思想。在实现方法上,以递归下降法为核心进行解析与计算。此外,三次作业还以迭代的形式对代码的耦合性与可扩展性进行了约束。在具体的实现过程中也蕴含着许多小的技巧方法,需要熟练掌握与灵活运用。
一.架构分析
1.UML图
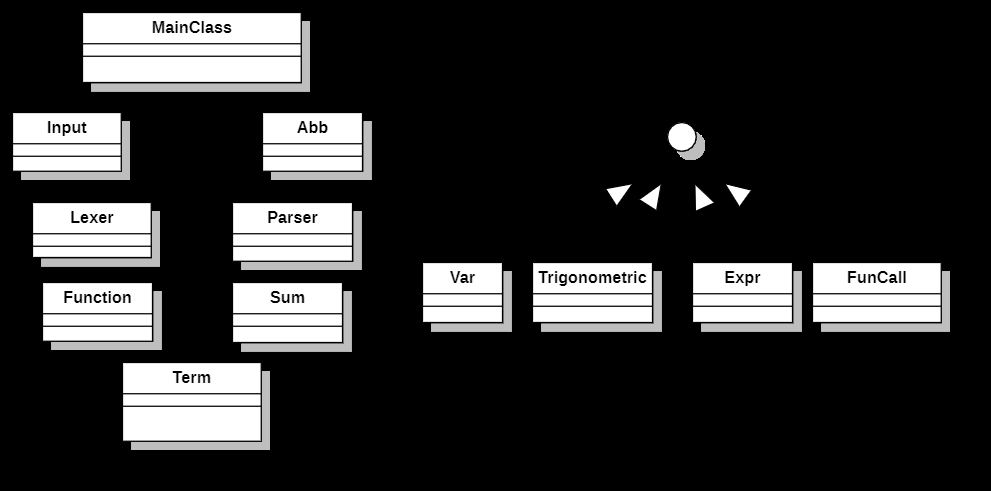
2.类的阐释
- Input
读入函数,构建Function对象;读入字符串,构建Abb对象进行预处理;
- Abb
对字符串进行五.实现细节1.字符串预处理中的操作,本质只是一个方法的集合;
- Lexer与Parser
相互配合解析字符串,本质以前缀为分割标志,采用递归下降法解析;
- Function与Sum
Function在Input被调用时构建对象,存储自定义函数的定义;Sum在字符串解析时建立,直接返回将i替换后的表达式因子;
- Term
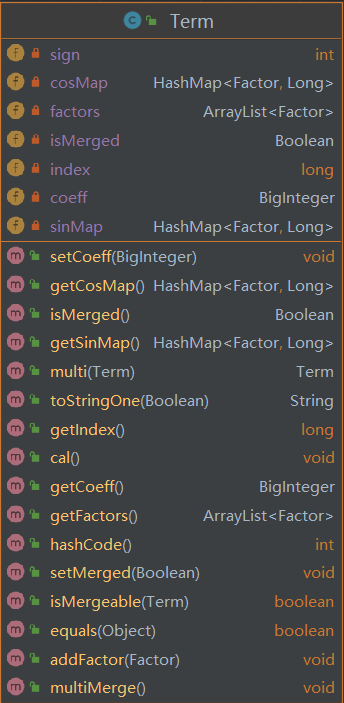
表示项,是最核心的类。包含了几乎所有基础的计算方法(项的乘法、加法、判断是否可合并等)。属性方面构建了两套数据结构,后面会有详细阐述;
-
Factor
因子类的抽象接口,包含统一的cal()抽象方法;
- Var
常数/幂函数类。指数为0时表示常数;
- Trigonometric
![]()
三角函数类。其中的cal()与induce()方法均为优化性能设计。cal()可以通过调用factor的cal()对内部factor进行化简,并判断如果该factor是表达式因子且仅包含一项且该项仅包含一个因子时,将该因子取代表达式因子、作为三角函数内部的因子;
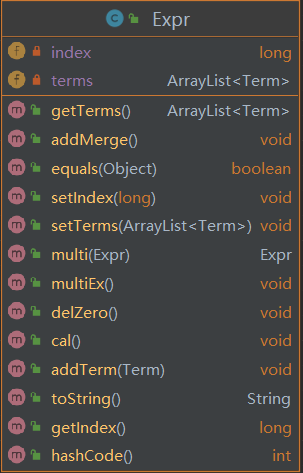
- Expr
![]()
表达式类。调用的各种方法实质都是对Term进行遍历、然后调用Term的方法;
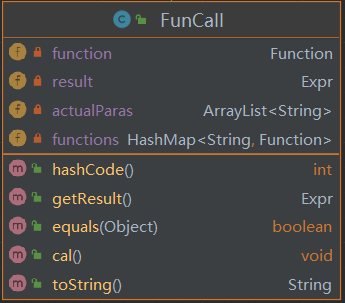
- FunCall
![]()
自定义函数调用类。在Parser解析到自定义函数的前缀f/g/h时构建,构建过程中直接利用Function中存储的属性计算得到调用替换后的表达式结果,并将表达式结果以字符串的形式返回。
3.度量分析
各类的方法度量分析如下:
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Abb.Abb(String) | 0 | 1 | 1 | 1 |
| Abb.exprAbb() | 0 | 1 | 1 | 1 |
| Abb.functionAbb() | 6 | 4 | 3 | 5 |
| Expr.addMerge() | 9 | 3 | 5 | 6 |
| Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| Expr.cal() | 6 | 1 | 4 | 4 |
| Expr.delZero() | 3 | 1 | 3 | 3 |
| Expr.equals(Object) | 4 | 3 | 3 | 5 |
| Expr.Expr(long) | 0 | 1 | 1 | 1 |
| Expr.getIndex() | 0 | 1 | 1 | 1 |
| Expr.getTerms() | 0 | 1 | 1 | 1 |
| Expr.hashCode() | 0 | 1 | 1 | 1 |
| Expr.multi(Expr) | 3 | 1 | 3 | 3 |
| Expr.multiEx() | 7 | 3 | 5 | 5 |
| Expr.setIndex(long) | 0 | 1 | 1 | 1 |
| Expr.setTerms(ArrayList) | 0 | 1 | 1 | 1 |
| Expr.toString() | 7 | 4 | 6 | 6 |
| FunCall.cal() | 0 | 1 | 1 | 1 |
| FunCall.equals(Object) | 3 | 3 | 2 | 4 |
| FunCall.FunCall(Function, ArrayList, HashMap) | 0 | 1 | 1 | 1 |
| FunCall.getResult() | 0 | 1 | 1 | 1 |
| FunCall.hashCode() | 0 | 1 | 1 | 1 |
| FunCall.toString() | 0 | 1 | 1 | 1 |
| Function.call(ArrayList) | 1 | 1 | 2 | 2 |
| Function.Function(String, ArrayList, String) | 0 | 1 | 1 | 1 |
| Input.getFunctions() | 0 | 1 | 1 | 1 |
| Input.getStr() | 0 | 1 | 1 | 1 |
| Input.Input(ExprInput) | 5 | 1 | 4 | 4 |
| Lexer.getInput() | 0 | 1 | 1 | 1 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getPara() | 7 | 6 | 6 | 6 |
| Lexer.getPos() | 0 | 1 | 1 | 1 |
| Lexer.getSum() | 18 | 3 | 9 | 12 |
| Lexer.getTriVar() | 7 | 3 | 4 | 5 |
| Lexer.Lexer(String, HashMap) | 0 | 1 | 1 | 1 |
| Lexer.next() | 3 | 2 | 2 | 3 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 0 | 1 | 1 | 1 |
| Parser.getExpr() | 9 | 3 | 4 | 6 |
| Parser.getFunc(String) | 1 | 1 | 2 | 2 |
| Parser.getPow() | 4 | 2 | 4 | 5 |
| Parser.getTrigonometric(int) | 5 | 3 | 3 | 4 |
| Parser.parseExpr() | 9 | 1 | 5 | 7 |
| Parser.parseFactor() | 16 | 5 | 11 | 12 |
| Parser.Parser(Lexer, HashMap) | 0 | 1 | 1 | 1 |
| Parser.parseStr() | 4 | 1 | 3 | 3 |
| Parser.parseTerm(int) | 1 | 1 | 2 | 2 |
| Sum.cal() | 4 | 1 | 3 | 3 |
| Sum.Sum(BigInteger, BigInteger, String) | 0 | 1 | 1 | 1 |
| Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| Term.cal() | 10 | 6 | 6 | 6 |
| Term.equals(Object) | 4 | 3 | 6 | 8 |
| Term.getCoeff() | 0 | 1 | 1 | 1 |
| Term.getCosMap() | 0 | 1 | 1 | 1 |
| Term.getFactors() | 0 | 1 | 1 | 1 |
| Term.getIndex() | 0 | 1 | 1 | 1 |
| Term.getSinMap() | 0 | 1 | 1 | 1 |
| Term.hashCode() | 0 | 1 | 1 | 1 |
| Term.isMergeable(Term) | 17 | 7 | 7 | 12 |
| Term.isMerged() | 0 | 1 | 1 | 1 |
| Term.multi(Term) | 8 | 1 | 5 | 5 |
| Term.multiMerge() | 38 | 9 | 10 | 12 |
| Term.setCoeff(BigInteger) | 0 | 1 | 1 | 1 |
| Term.setMerged(Boolean) | 0 | 1 | 1 | 1 |
| Term.Term(int) | 0 | 1 | 1 | 1 |
| Term.toStringOne(Boolean) | 34 | 1 | 15 | 20 |
| Trigonometric.cal() | 34 | 1 | 16 | 18 |
| Trigonometric.equals(Object) | 4 | 3 | 4 | 6 |
| Trigonometric.getFactor() | 0 | 1 | 1 | 1 |
| Trigonometric.getIndex() | 0 | 1 | 1 | 1 |
| Trigonometric.getType() | 0 | 1 | 1 | 1 |
| Trigonometric.hashCode() | 0 | 1 | 1 | 1 |
| Trigonometric.induce() | 23 | 10 | 8 | 13 |
| Trigonometric.toString() | 3 | 1 | 3 | 3 |
| Trigonometric.Trigonometric(Factor, long, int) | 0 | 1 | 1 | 1 |
| Var.cal() | 0 | 1 | 1 | 1 |
| Var.equals(Object) | 4 | 3 | 3 | 5 |
| Var.getCoeff() | 0 | 1 | 1 | 1 |
| Var.getIndex() | 0 | 1 | 1 | 1 |
| Var.hashCode() | 0 | 1 | 1 | 1 |
| Var.setCoeff(BigInteger) | 0 | 1 | 1 | 1 |
| Var.toString() | 7 | 1 | 5 | 6 |
| Var.Var(BigInteger, long) | 0 | 1 | 1 | 1 |
| Total | 330 | 150 | 235 | 280 |
| Average | 3.975904 | 1.807229 | 2.831325 | 3.373494 |
其中,加粗部分为复杂度过高的方法。
经过分析发现,检测出复杂度过高的方法主要存在以下问题:
- 耦合性过强。对于类中其它方法或其它类的方法依赖性强;
- if-else嵌套过多。为优化性能对许多情况进行具体讨论;
综上,在今后的设计中应当更加注重类的划分,减少类与类之间的依赖;同时提高类的抽象层次,避免陷于过于细节的分类讨论。
二.核心方法
在笔者的三次作业中,最核心的方法是递归下降法。
个人认为,结合三次作业,递归下降法具有以下特征:
- 递归下降法适用于构建“嵌套式”数据结构。三次作业的题目背景——表达式,即是非常典型的嵌套结构。一方面,嵌套的对象类型众多,且会出现外层类型嵌套内层类型、内层类型又嵌套外层类型的结构(如因子中包含表达式因子,三角函数因子包含各类因子等);另一方面,嵌套的层数并没有限制,具有较大的“未知性”。因此使用常规的字符串解析/正则表达式匹配并不可取。而递归下降法适用于具有上述特征的数据形式。
- 递归下降法适用于“嵌套式”调用方法。三次作业中,除了在解析时运用了递归下降法,还在各类因子、项的计算中运用了递归下降法。由递归下降法构造出的数据结构也具有嵌套的性质,在调用各种计算方法时需要考虑到构建的数据结构的嵌套性。因此在调用方法时仍需采取递归下降法进行调用。
- 递归下降法要求对象必须具有较好的封装性与低耦合性。每次递归下降地进行下一层的解析或者调用下一层的方法时,一个基本要求便是不能对上一层的对象状态造成破坏。如果设计的对象没有较好的封装性与低耦合性,递归调用处理下一层时破坏了上一层的状态,当调用结束返回时,原有的方法面对错误的状态必然会导致错误的结果。
- 递归下降法使得方法的构建不必牵累于类间的嵌套关系。当做好上一点所说的保证对象的封装性与低耦合性后,递归下降的优势也便凸显出来:方法的大部分设计只需考虑类本身的属性即可,嵌套的部分仅需一行调用被嵌套类相应方法的代码即可,非常简便。
此外,正如上面提及的,在三次作业中,表达式的解析与计算都运用了递归下降法。
三.设计思想
1.面向对象设计方法
由于在构建对象的过程中,直接将现实中的表达式、项、各类因子等构建了相应的类。因此在构造展开、化简的方法时,很自然的可以将现实中表达式的展开、化简过程映射到方法的构造中。这也正是面向对象构造与设计的一大优势:在建立位于“解空间”的机器模型和位于“问题空间”的实际待解问题模型的映射时代价较低,仅需对实际待解问题模型中的对象进行合理的划分与抽象即可。
2.面向方法构建数据结构
个人认为,不同的数据结构方便于不同的方法。在解决实际问题中往往需要构造许多方法。因此,当构建的数据结构不便于方法的实现时,应当适时的对现有的数据结构进行转换或重新构建,以适用于不同的方法。
如在本单元的作业中,我们需要对表达式进行解析与计算。利用递归下降法建立的“嵌套式”数据结构便于解析却不便于计算,因此需要构建一套新的数据结构便于表达式计算方法的实现。
对于新数据结构的构建,既可以构建一个新的类,也可以在原有的类增添属性、在同一类中构建两套数据结构。个人在三次作业中采用了后面的方案,因为原类的数据都已经得到较好的封装,如果另建一个新类还需要相应地构造在类间传递数据的get()/set()方法,较为繁琐。
基于以上思想,自然衍生出以下三个问题:
- 构建一种与原数据结构包含信息完全等价的新数据结构
- 构造利用新数据结构进行表达式计算的计算方法
- 构造由原数据结构向新数据结构的转换方法
对于三个问题具体解决过程的实例,可以参照:
讨论:关于数据结构构建的一点思考 - 第二次作业 - 2022面向对象设计与构造 | 面向对象设计与构造 (buaa.edu.cn)
3.使用接口提高抽象层次
使用接口,可以极大的提高类的抽象层次,有利于提高可扩展性。
在三次作业中,笔者使用了Factor接口,各类型的因子作为Factor的实现。这样使得在高一层的类中观察各因子时,无需纠结于它们具体是哪一类具体的因子,只需在更高抽象层次上的Factor对它们进行构建与调用。此外,当有新的具体的因子类加入时,只需将其作为Factor的又一实现,而无需改变高一层类中的处理过程,提高了可扩展性。
4.自结果向问题设计
在三次作业的题目叙述中,概念较多且细节复杂,从问题入手很容易一上来就拘泥于各种细节而忽视整体。但对于表达式展开化简后的结果是十分清晰的。
因此,笔者采用了所谓“自结果向问题”的设计思路,即:先假定自己已经对输入的字符串作好了解析,得到了Expr->Term->Factor的嵌套数据结构,然后直接基于假定得到的数据结构进行转化、计算,最后再写字符串解析的相关代码,真正实现之前的假设,完整地从头到尾串联起来。
其实除了这种大方向上的假设,在构造具体的方法时也可以采取这样的思路,如:在构建Term的multi()方法时,假定已经得到了Term的系数、指数、三角函数的HashMap等,基于假设写出multi()方法,然后再设法实现假设;在构建合并同类项的方法时,先假定自己已经构建好判断同类项的方法,基于假设写出可合并状态下系数相加、重新加入ArrayList等过程,最后再设法实现假设……确定好每一个步骤的dependency与target,可以避免自己过早地陷入细节,可以使自己对全局的设计始终保持清晰的认识与把控。
四.迭代历程
基于三.设计思想的内容,三次作业的迭代过程,实质上是三次数据结构的迭代与重构过程。每次作业因子的类别越来越多,化简后得到的最终形式也越来越复杂,因此需要相应的调整现有的数据结构,相应的方法也随之变动。
下面介绍笔者三次作业的面向计算方法的数据结构,并简述相应方法的设计。
1.hw1
-
Expr
private BigInteger[] coefficient; -
Term
private BigInteger coefficient; private int index;
由于hw1中只出现了幂函数,所以对于表达式,其最终结果一定为系数0+系数1*x+系数2*x**2+...+系数8*x**8的形式,因此仅需构建一个大小为9的数组:下标表次数,值表系数。相应的,项的合并方法也十分简便,仅需在次数对应下标的值内加项的系数即可。
2.hw2
-
Term
private BigInteger coeff; //coefficient private long index; //index ////////// private long[] sinIndex; private long[] cosIndex; //index stands for x's index, value stands for sin's index ////////// private HashMap<BigInteger, Long> sinCoeff; private HashMap<BigInteger, Long> cosCoeff; //key stands for const, value stands for index
下面依次阐释
-
对于
系数*x**指数的形式,系数和指数是必须记录信息。对于其中的x,由于作业限制只会出现x一种自变量,相当于自变量只有x一种状态。对于只有一种状态的变量无需记录,否则会造成信息冗余。 -
继承上面的思路,对于
sin(x)**指数1*sin(x**2)**指数2*...*sin(x**8)**指数8,由于作业限制sin内的自变量只可能是x,x**2...x**8,所以可以只记录指数1~指数8八个会变化状态的信息。若有sin缺失则给对应指数值赋值为0即可。e.g. sin(x**2)**3*sin(x**5)**2 ->
-
cos同理。
-
对于
sin(常数1)**指数1*sin(常数2)**指数2*...,各项常数指数均不相同且有对应关系。使用HashMap的键存储常数,值存储指数。由于HashMap按键值有序排列。这样存储既保证了常数与指数的对应关系,还方便了后续判断两个项是否为同类项。 -
cos同理
3.hw3
-
Term
private BigInteger coeff; private long index; private HashMap<Factor, Long> sinMap; private HashMap<Factor, Long> cosMap;
与hw2相比,最大的不同在于sin与cos内部可能为各类因子。因此此时无法以幂函数的指数作为HashMap的key,而是直接以Factor本身作为HashMap的key。注意此时需要对应的重写hashcode()与.equals()方法。关于这点在五.实现细节中还会有详细阐述。
4.小结
从上面三次作业的迭代过程中不难看出,倘若一开始设计的数据结构具有较好的普遍性与可扩展性,则迭代开发也会变得比较轻松。但更具普遍性的数据结构,其相应的方法也更难构建。个人认为这是一个需要斟酌权衡的地方。
而在笔者的迭代过程中,过于注重减少信息冗余以实现方法构建的简便性,因此在每次迭代的过程中进行了较多的重构。这是笔者在以后的作业中应当继续磨练避免的事情。
五.实现细节
1.字符串预处理
为了便于进一步的解析,可以将读入的字符串进行如下预处理:
- 去掉所有空格/Tab
- 将所有连着的符号合并。如
+++->+,+-+->-等 **->^sin->scos->csum->a
2.Lexer与Parser
Lexer与Parser的具体实现方法,在训练栏目中已经给出了很好的示例。个人的理解:Lexer是以字符单元为单位进行处理,便于Parser构建逻辑上的数据结构联系。
此外,Parser判别当前解析的是表达式/项/各类因子的依据,实际是以各自字符串的前缀为划分依据的。以Factor为例,如下图所示:

可以看到,在完成五.1中的预处理之后,六种因子的前缀分别为+/-/数字、x、s/c、f/g/h、a、(,各不相同,可作为划分依据。
3.判断同类项
判断不同的项是否为同类项,即需比较x的指数、sin各项、cos各项。注意在比较sin/cos时既需比较factor也需比较指数。
在比较factor相等时,需要重写hashcode()与.equals()方法。此时使用IDEA自带的重写方法、选中关心的属性作为相等的依据即可。
Java基础常见知识&面试题总结(上) | JavaGuide
4.优化细节
个人认为比较容易实现的性能优化的点
x**2->x*x(注意三角函数中自变量须保持x**2)- 正项提前
- 系数指数“1”省略
- 利用三角函数奇偶性去掉自变量符号,同时注意外部幂次的奇偶性
sin(0)->0,cos(0)->1- sin/cos中若为表达式因子且仅包含一项且该项仅包含一个因子时,将该因子取代表达式因子、作为三角函数内部的因子
此外还有三角函数的平方和公式、二倍角公式等。但三角函数水太深了,还是应当在保证正确性的前提下追求性能。
六.常见bug
以下是笔者三次作业时遇到的一些bug:
- 遍历容器时修改容器;
- 误将浅拷贝用作深拷贝;
以上两点是在乘法展开时遇到的问题。笔者采用的解决方案是建立一个新的容器,将新的元素或无需删除的元素加入新容器,将需要删除的元素不加入新容器,最后再将原容器变量名指向新容器即可。
- 判断同类项时只比较了sin/cos内部的factor,未比较外部的指数;
- 判断字符串相等时误用
==,应用.equals(); - BigInteger调用add()方法后没有再赋值给自己;
后三个问题较为细节,也有自己掌握不熟练的原因,发现后更正即可。
七.hack策略
先贴一张笔者hw3的hack“成果”(
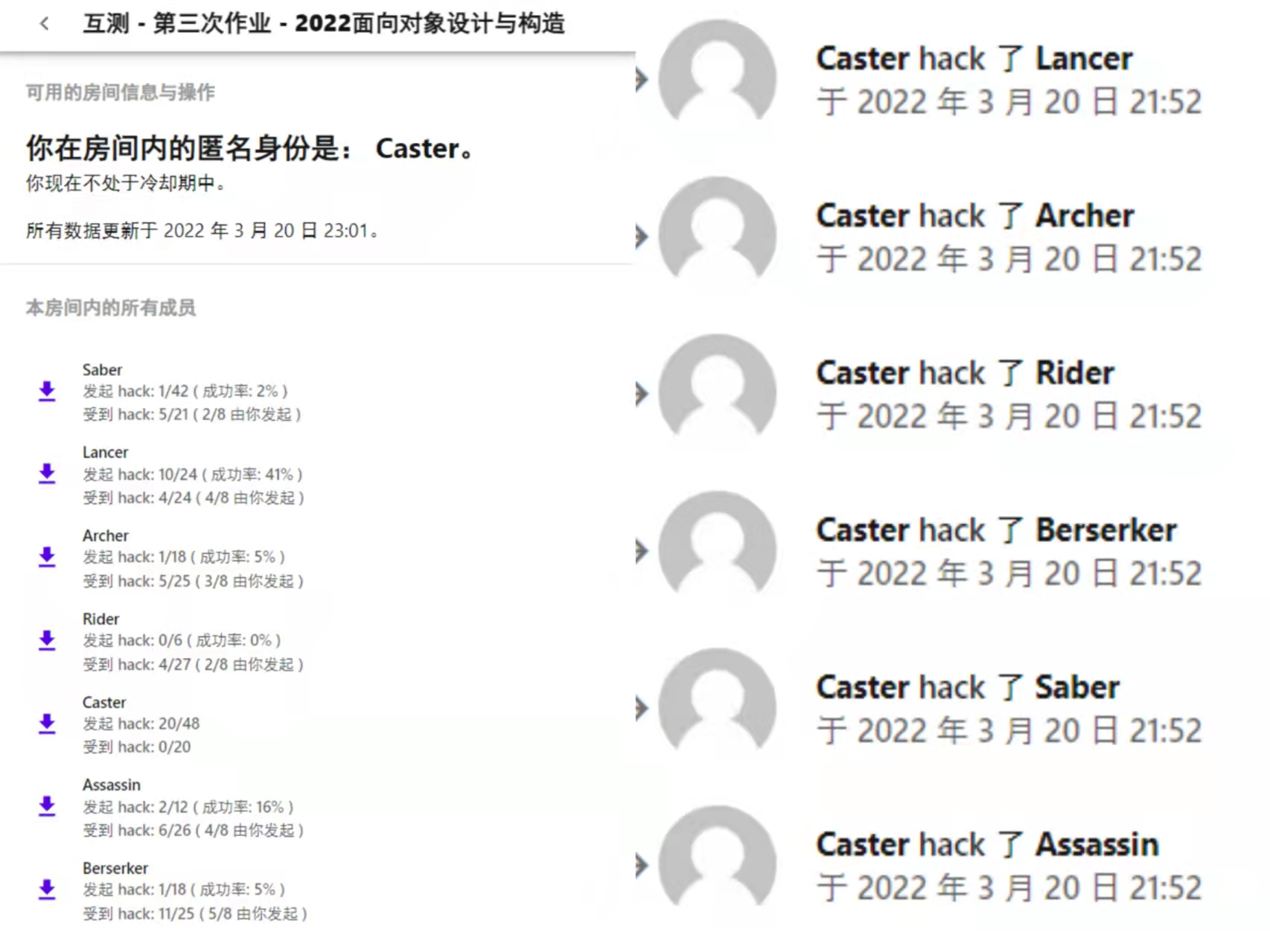
平心而论,hack的确有很大的运气成分在里面。不过也有一些通用的策略:
- 全面性测试。首先针对所有的代码进行全面性测试,观察输出行为是否存在有关的化简优化;
- 针对不同的输出行为,构造特定样例。如对于进行了三角函数正负号化简的代码,可以测试sin/cos奇偶次幂的不同样例,观察结果是否正确;
- 阅读代码。对于将字符串简单匹配、替换的行为着重关注,观察是否考察全面;
- 边界数据构造。如超int范围大数字、多层函数嵌套等。
此外,在hack过程中阅读他人的代码也可以学习到他人的一些巧妙设计,可以适当地借鉴学习。
八.真情实感的心得体会
真情实感地吐槽一句真的太肝了呀。对于Java零基础的笔者,从菜鸟教程的基础语法学起勉强搞完了两个pre;还没太消化完全又是一周一迭代的堪比数据结构大作业的每周作业。很多东西现查现学现用,一直被任务push。一周七天都有各自的安排,感觉每天都在coding...
首先非常感谢老师和助教们设计的“训练栏目”,给三次作业的实现起到了很好的启发式作用。自己在迭代任务的push之下也确实真正体会到一些面向对象设计的思想。也非常感谢每天一起coding的三位hxd,相互交流学习共同进步。
但与此同时,笔者深感自己对于面向对象的理解依然过于浅显。在Thinking in Java一书中,作者认为:
每个对象看起来都有点像一台微型计算机——它具有状态,还具有操作,用户可以要求对象执行这些操作...
读到这里,隐约感觉作者对于对象的描述与上学期计组课程设计的mips微系统很像:它们都具有状态与操作,并且可以根据自身的状态与外部的请求执行特定的操作。可惜在第一单元的实现过程中,笔者并未在实践过程中体会到内部状态对于行为操作的影响。
此外,类的抽象、各种设计原则、容器的灵活使用……依然需要后续大量的训练去逐步体会琢磨。希望自己能在老师、助教和同学的帮助下继续进步~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号