二分图

被老师和那两个**逼的做的证明

最大子集，及二分图扩充

二分图

一、二分图概念

就相当于把所有的点分成了两个阵营，其中所有的边都必须从一个阵营连向另一个阵营

二、最小覆盖/最大匹配

A.最大匹配

定义：在一个无向图中，定义一条边覆盖的点为这条边的两个端点。

找到一个边集S包含最多的边，使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。

换句话说，就是找最多的边，然后每个点最多只有一条边出去。

通俗地讲，比如说有一场宴会，男孩和女孩跳舞，并且他们必须互相喜欢才能一起跳舞，一个男孩可能喜欢0个或多个女孩，一个女孩也可能喜欢0个或多个男孩，但一个男孩和他喜欢地女孩跳舞之后就不能和其他他喜欢地女孩跳舞，女孩亦是如此。请问最多可以多少对男孩女孩一起跳舞。

很显然，互相喜欢的男孩和女孩建边得到一个二分图，求一个一个边集S包含最多的边，使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。即求二分图的最大匹配。

怎么找呢，其实和B一样，用xyl

我们以下图为例说明匈牙利匹配算法。

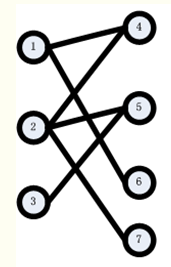
step1：从1开始，找到右侧的点4，发现点4没有被匹配，所以找到了1的匹配点为4 。得到如下图：

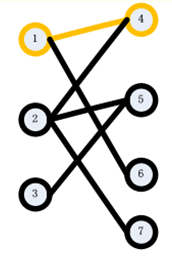
step2：接下来，从2开始，试图在右边找到一个它的匹配点。我们枚举5，发现5还没有被匹配，于是找到了2的匹配点，为5.得到如下图：

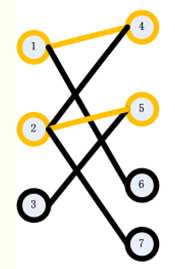
step3:接下来，我们找3的匹配点。我们枚举了5，发现5已经有了匹配点2。此时，我们试图找到2除了5以外的另一个匹配点，我们发现，我们可以找到7，于是2可以匹配7，所以5可以匹配给3，得到如下图：

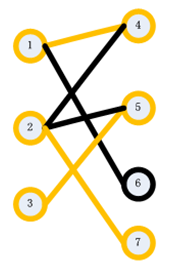
此时，结束，我们得到最大匹配为3。

B最小顶点覆盖

定义：最小顶点覆盖就是选择最少的点来覆盖所有的边。

方法：最小顶点覆盖等于二分图的最大匹配。

我们用二分图来构造最小顶点覆盖。

其实就是上面的，不理解的可以问一问或看一看这里的

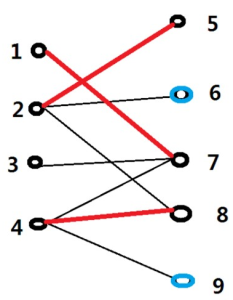
对于上面这个二分图，顶点分为左右两个集合，X集合包含1,2,3,4，Y集合包含5,6,7,8,9.假如现在我们已经找到一个最大匹配M，就是上面的红线所标注的M={(1,7),(2,5),(4,8)}。我们作如下定义：（1）定义1、2、4、5、7、8为已经匹配过的点，其他点为未匹配的点；（2）定义(4,8)、(1,7)、(2,5)为已匹配的边，其他边为未匹配的边。

下面我们从Y集合中找出未匹配的点，就是上面标记的6和9。每次我们从右边选出一个未匹配的点，从该点出发， 做一条未匹配边->匹配边->未匹配边->……->匹配边（注意最后以匹配边结尾），并且标记用到的点，得到下图：

其中紫色的边为我们刚才画的边，其中标记的点有2、4、5、6、8、9。 上图的两条路为：（1）9->4->8->2->5 （2）6->2->5。这两条路都是未匹配边->匹配边->未匹配边->……->匹配边。（注意如果一个右侧未匹配点有多条边，那么这样的从该点开始的路径就有多条，上面的6和9都只有一条边，所以从每个点开始的这样的路径只有一条）。

现在我们将左侧标记的点2、4和右侧未标记的点7选出组成集合S， 那个S就是一个最小顶点覆盖集，就是S集合可以覆盖所有的边。下面证明：

（1）|S|=M，即最小顶点覆盖等于二分图最大匹配：左边标记的点全都为匹配边的顶点，因为我们构造路径的时候左边的点向右找的边都是最大匹配的边；右边未标记的点也为二分图最大匹配边的顶点。而且左边标记的加上有边未标记的正好是最大匹配的数目。

（2）S能覆盖所有的边。所有的边可以分为下面三种情况：a、左端点标记、右端点标记；这些边一定被左侧标记的点覆盖，比如上面的2,4；b、右端点未标记；这些边一定被右侧未标记的点覆盖，比如上面的7；c、左端点未标记、右端点标记。

下面我们证明c这种边压根就不会存在：若c是最大匹配中的边，由于右端点不可能是一条路径的起点（因为我们的起点都是从Y集合中未匹配的点开始的），于是右端点的标记只能是在构造中从左边连过来，这是左端点必定被标记了，这时c就转化成了a；若c属于未匹配边，那么左端点必定是一个匹配点，那么c的右端点必定是一条路径的起始点，因此c的左端点也会成为一条路径的第二个点而被标记，这时c也就成了a。所以c这种边肯定是不存在的。

（3）S是最小的顶点集：因为最大匹配为M，而|S|=M，所以如果S中的点再少，那么连M个匹配的边都不能覆盖。

详见：二分图的最小顶点覆盖 最大独立集 最大团 - 朝拜明天19891101 - 博客园 (cnblogs.com)

当然这不是这道题重点，关键在于

三、最大独立集

二分图的最大独立集

定义：选出一些顶点使得这些顶点两两不相邻，则这些点构成的集合称为独立集。找出一个包含顶点数最多的独立集称为最大独立集。

方法：最大独立集=所有顶点数-最小顶点覆盖的顶点数

为什么这个是正确的呢，可以来稍微证明一下

假设我现在已经有了最小顶点覆盖

我删掉这些点，假设剩下的点左右还有链接

那很明显，这一条边是没有被最小顶点所覆盖的

那按照定义，我们假设的最小顶点覆盖就不成立了，那么就反证出了上面是成立的

那怎么确保是最大的呢？

最小点覆盖…..

最小…

小…

…

然后就完了

联系

现在再来看看这个东东和二分图有peach关系

首先可以发现两个奇数或者两个偶数都可以满足这个性质（毕竟有+1，奇数也会变偶数）

然后发现数字(自然数)不是偶数就是奇数（如果你发现不只的话，建议尽早退出竞赛去学数学……)

那么为什么会想到最大独立集呢

先看最大独立集定义：选出一些顶点使得这些顶点两两不相邻，则这些点构成的集合称为独立集。找出一个包含顶点数最多的独立集称为最大独立集。

也就是说，只要它们之间没有边，他们就可以选到一个集合里

而这个边，可以抽象的看成一种规则

什么叫“规则”，你看，我连了两个点的边，那两个点就只能二选一了….通过这个性质就可以给我们的二分独立集加性质

就如这道题，我让连着的两条边只要不符合要求就连上一条边(当然两个阵营内部不需要，因为他们两两满足要求，也就是说，我最少最少也可以选择一边的所有点作为ans)，然后求最大独立集，那么我的集合中最终都是满足要求的，并且是最大的

其他

这种题要很精致的思考能力，特别是抽象能力，这也给了我们更多的思考方向；

不会？想想图吧…