ProtoGate 的理论分析部分
在论文《ProtoGate: Prototype-based Neural Networks with Global-to-local Feature Selection for Tabular Biomedical Data》中作者对理论结论给出了分析过程,这篇博客对该部分进行阅读和记录。
| 论文概况 | 详细 |
|---|---|
| 标题 | 《ProtoGate: Prototype-based Neural Networks with Global-to-local Feature Selection for Tabular Biomedical Data》 |
| 作者 | Xiangjian Jiang, Andrei Margeloiu, Nikola Simidjievski, Mateja Jamnik |
| 发表会议 | The 41st International Conference on Machine Learning (ICML 2024) |
| 发表年份 | 2024 |
| 会议等级 | CCF-A |
| 论文代码 | https://github.com/SilenceX12138/ProtoGate |
作者单位:
- Department of Computer Science and Technology, University of Cambridge, UK
- Department of Oncology, University of Cambridge, UK.
预备知识
Q 函数
Q 函数的完整名称是标准正态分布的右尾概率函数。其定义为:对于一个服从标准正态分布(均值为 0,方差为 1)的随机变量 $ Z \sim \mathcal{N}(0, 1) $,Q 函数计算的是 $ Z $ 的取值大于某个给定阈值 $ x $ 的概率:
其中,$ P $ 表示概率。从几何角度看,Q 函数计算的是标准正态分布概率密度函数曲线下,从 $ x $ 到正无穷大(+∞)之间的面积。整个钟形曲线下的总面积为1,代表概率为 100%,$ Q(x) $ 就是右尾阴影区域的面积。根据其几何定义,Q 函数可以写为积分形式:
其中,\(\frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}}\) 是标准正态分布的概率密度函数,$ x $ 是积分的下限,$ t $ 是积分变量。这个积分没有简单的闭式解析解,因此其值通常通过查表、数值计算或使用近似公式获得。
标准正态分布的累积分布函数 通常用 $ \Phi(x) $ 或 $ F(x) $ 表示,其定义为:
$ \Phi(x) $ 表示的是左尾加上中间部分直到 $ x $ 的总面积。由于整个曲线下的面积为 1,Q 函数和累积分布函数之间存在互补关系:
排序矩阵
对于一个包含 N 个原型的集合,其排序结果可以用一个硬排列矩阵 \(P \in \{0,1\}^{N \times N}\) 来表示。它是一个双随机矩阵(每行、每列的和均为1),并且满足:
例如,如果第 3 个原型是最近邻(排第 1 位),则 \(P[1,3] = 1\),矩阵中其他元素为 0。可微排序器(如 NeuralSort)的目标是计算一个松弛的(软)排列矩阵 \(\widehat{P} \in [0,1]^{N \times N}\)。它也是一个双随机矩阵,但元素是连续的。\(\widehat{P}[n, m]\) 可以理解为第 m 个原型被排在第 n 个位置的概率。
局部特征掩码 L0 范数估计
正文中的公式(1)是 ProtoGate 理论框架的核心,它建立了局部特征掩码的 L0 范数与一个可微的近似函数之间的联系,从而使得基于梯度下降的优化成为可能。ProtoGate 的目标是优化局部特征掩码 \(s_{\text{local}}^{(i)}\) 的稀疏性,即最小化其 L0 范数 \(\left\|s_{\text{local}}^{(i)}\right\|_0\),它等于向量中非零元素的个数:
其中,\(\mathbb{I}(\cdot)\) 是指示函数。关键问题在于:指示函数的导数几乎处处为零或无穷,导致整个表达式不可微,无法直接用于梯度下降。为了解决不可微问题,ProtoGate 采用了概率松弛策略,通过引入高斯噪声将确定的掩码重新定义为一个随机变量:
其中,\(\mu^{(i)}\) 是门控网络输出的确定性向量,\(\epsilon^{(i)}\) 是注入的高斯噪声。此时优化目标从最小化确定的 L0 范数,转变为最小化其数学期望:
根据数学期望的线性性质,求和符号可以移到期望外面:
由于一个指示函数的期望等于其对应事件发生的概率:
因此目标可以简化为:
现在需要计算概率 \(\mathbb{P}\left( s_{\text{local}, d}^{(i)} > 0 \right)\)。根据掩码的定义,因为裁剪函数 \(\max(0, \cdot)\) 保证输出非负,且大于零的条件取决于内部变量是否大于零。所以当且仅当 \(\mu_d^{(i)} + \epsilon_d^{(i)} > 0\) 时事件 \(s_{\text{local}, d}^{(i)} > 0\) 发生。由于 \(\epsilon_d^{(i)} \sim \mathcal{N}(0, \sigma^2)\),所以 \(\mu_d^{(i)} + \epsilon_d^{(i)} \sim \mathcal{N}(\mu_d^{(i)}, \sigma^2)\)。\(\Phi(\cdot)\) 是标准正态分布的累积分布函数,则求这个正态分布变量大于 0 的概率:
如果是按照论文中的推导方法,对不等式进行简单的代数变换:
所以,概率 \(\mathbb{P}\left( s_{\text{local}, d}^{(i)} > 0 \right)\) 等价于:
由于随机噪声 $ \epsilon^{(i)}_d $ 服从均值为0、标准差为 $ \sigma $ 的正态分布,即 $ \epsilon^{(i)}_d \sim \mathcal{N}(0, \sigma^2) $。为了使用标准正态分布的性质,将不等式两边同时除以标准差 $ \sigma $。由于 $ \sigma > 0 $,不等号方向不变。
定义一个新的随机变量 $ Z_d = \frac{\epsilon^{(i)}_d}{\sigma} $。由于 $ \epsilon^{(i)}_d $ 服从 \(\mathcal{N}(0, \sigma^2)\) ,那么根据正态分布的性质,$ Z_d $ 就服从标准正态分布,即 $ Z_d \sim \mathcal{N}(0, 1) $。则概率表达式变成了:
由于 Q 函数计算的是标准正态随机变量大于某个值的概率,即 $ Q(x) = P(Z > x) $,可以直接将上述概率写为:
因此,整个概率表达式推导为:
根据定义,标准正态分布的 Q 函数的积分形式为:
其中被积函数 \(\frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}}\) 是标准正态分布的概率密度函数。将 \(x = -\frac{\mu^{(i)}_d}{\sigma}\) 代入上面的积分定义,得到:
因此,原始的公式可以展开为如下积分形式:
将上述过程整理一下,即可得到本文附录中 D. Theoretical Analysis 的公式(4)的形式。
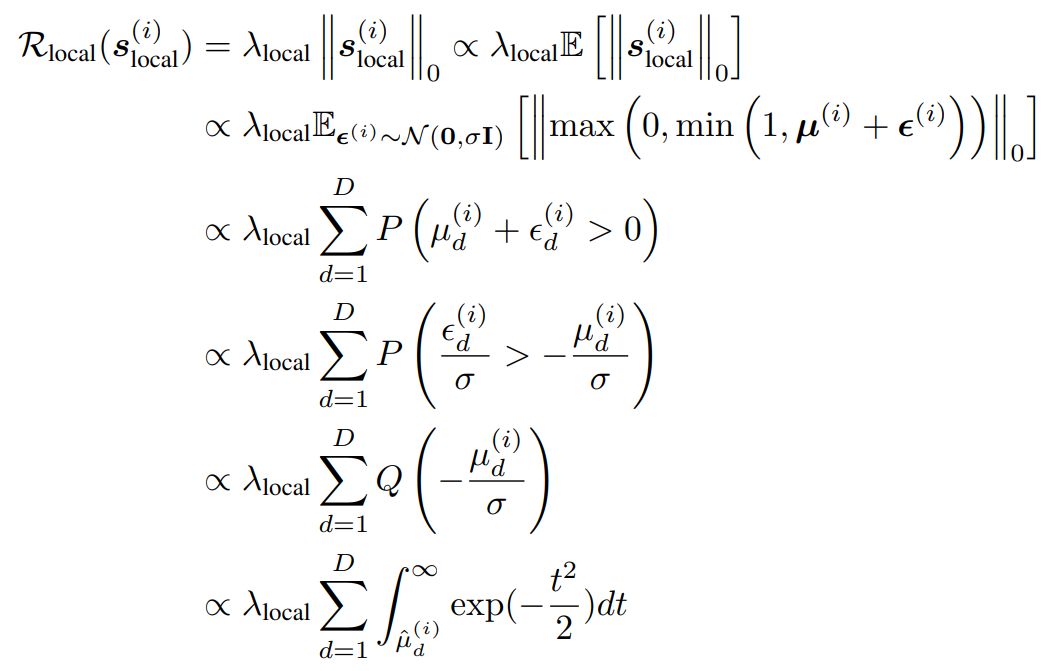
在实际实现中,\(\Phi(\cdot)\) 常用其解析近似,例如 sigmoid 函数 来替代。因此,正则化项在代码中通常表现为:
排列矩阵 P 的估计
以 NeuralSort 方法为例,其推导基于一个关键的数学洞察:排序行为可以通过计算元素间的差异来表征。从排序的数学本质来说,对一组值进行排序,等价于确定一个排列\(\tau\),使得对于任意位置排名\(i < j\),都有值 \(s_{\tau(i)} \ge s_{\tau(j)}\)。这可以转化为一组不等式约束。给定一个输入向量 \(s = [s_1, s_2, ..., s_N]^T\)(例如,查询样本与各原型距离的负值,因为需要找最小值),软排列矩阵的第 \(n\) 行(对应排名第 \(n\) 的位置)可以通过以下方式计算:
其中,\(s \mathbf{1}^T - \mathbf{1} s^T\) 计算了所有元素对之间的差值,得到一个\(N \times N\)的矩阵\(A\),其中\(A[i,j] = s_i - s_j\)。\(|A|\) 取了绝对值,\(|s_i - s_j|\) 的大小反映了 \(s_i\) 和 \(s_j\) 的相对次序关系。\(\text{softmax}\) 函数将最终的差异映射为一个概率分布。该公式除以一个温度参数\(\tau\) 来控制分布的“软硬”程度:
- 当 \(\tau \to 0\),\(\text{softmax}\)的输出会接近一个one-hot向量,\(\widehat{P}\) 趋近于真实的硬排列矩阵。
- 当 \(\tau \to \infty\),\(\widehat{P}\) 趋近于均匀分布。
在 ProtoGate 中,可微排序器的输入向量 \(s\) 是查询样本与原型库中所有原型的负欧氏距离:
使用负距离是因为排序通常是降序找最大值,而我们需要的是距离最小(即负值最大)的原型排名靠前。
Lemma D.2.
排列矩阵 P 的估计的推导的一个理论基础是证明这个松弛是合理的。论文引用了 Grover et al.(2018)的结论:在温和的条件下,当温度参数\(\tau \to 0\)时,软的排列矩阵 \(\widehat{P}\) 会几乎必然地 收敛到硬的排列矩阵 \(P\):
这保证了软排序是硬排序的一个有效且一致的近似,即本文的 Lemma D.2.:

Definition D.1
Definition D.1 的核心目标是为“排序”这个离散操作建立一个连续的、可微的数学表示。在 ProtoGate 中,排序是为了找到与查询样本最相似的 K 个原型。标准的排序算法(如快速排序)是离散且不可微的,会阻碍梯度反向传播,因此需要一种可微的近似。
该定义通过几个数学构件来描述如何计算一个软的排列矩阵(Soft Permutation Matrix)。定义给定一个向量 \(v \in R^N\),其中每个元素 \(v[n]\) 表示查询样本与第 \(n\) 个原型之间的相似性(例如负欧氏距离)。接着构建绝对差异矩阵 \(A \in R^{N \times N}\),其中每个元素 \(A[n, m]\) 是向量 \(v\) 中第 \(n\) 个和第 \(m\) 个元素差值的绝对值。这个矩阵捕获了所有原型两两之间的相似性差异。
基于上述构件,排列矩阵 \(P\) 被定义为:
其中,\(\mathcal{P}_N\) 是所有 \(N \times N\) 置换矩阵(Permutation Matrices)的集合。置换矩阵是每行和每列只有一个 1,其余为 0 的方阵。\(\operatorname{Tr}(\cdot)\) 表示矩阵的迹,即主对角线元素之和。矩阵 \(P^T A\) 的迹计算如下:
由于 \(P\) 是置换矩阵,\(P[j, i] = 1\) 当且仅当在排列中,第 \(j\) 个元素被分配到了第 \(i\) 个位置。因此,上述求和实际上是在计算:对于排列 \(P\) 所确定的顺序,所有处在特定对应位置上的元素对 \((v_j, v_i)\) 的差异值 \(A[j, i]\) 的总和。这个优化问题的解 \(P\) 就是一个硬排列矩阵,它编码了将向量 \(v\) 中的元素按从大到小排序所需的置换关系。最大化 \(\operatorname{Tr}(P^T A)\) 的直观意义是:寻找一个排列 \(P\),使得在这个排列下,被“配对”起来的元素之间的差异值之和最大。
这个定义的本质是将“排序”重新表述为一个线性分配问题(Linear Assignment Problem)。目标是找到一个置换(即排列矩阵 \(P\)),使得某种“代价”或“收益”最大化。在这里,“收益”被定义为 \(\operatorname{Tr}(P^T A)\)。矩阵 \(A\) 编码了所有元素对的“差异强度”,通过最大化 \(\operatorname{Tr}(P^T A)\),我们实际上是在寻找一个排列,使得在这个排列的视角下,元素间的差异被最大限度地体现出来。因此排序就是为了清晰地展现元素间的序关系(差异),所以该定义恰好与排序的目标一致。
Theorem D.3.
Theorem D.3 的表述为:在给定的上下文下,ProtoGate 的预测损失(公式 2)估计的是,在查询样本的 K 个最近邻原型中,与其类别不同的原型数量。这意味着,当模型最小化这个损失时,它实质上是在减少错误近邻的数量,或者说增加正确近邻的数量。这直接优化了 K 近邻分类器的核心目标。
在推导之前,需要明确几个关键元素:
| 元素 | 符号 | 含义 |
|---|---|---|
| 软排列矩阵 | \(\widehat{P}\) | 一个 \(N \times N\) 的行随机矩阵,由可微排序(如 NeuralSort)产生。\(\widehat{P}[n, m]\) 表示第 \(m\) 个原型是第 \(n\) 个最近邻的“概率”。 |
| 原型标签向量 | \(Y_{\mathcal{B}}\) | 一个 \(N \times 1\) 的向量,包含了原型库中所有原型样本的真实标签。 |
| 查询样本标签 | \(y_{\text{query}}\) | 当前需要分类的样本的真实标签。 |
论文中公式(2)给出的损失函数为:
其中,\(\mathbb{E}_{\widehat{P}[n,:]}\) 表示基于分布 \(\widehat{P}[n,:]\) 求期望。这个公式可以理解为:对于排序后的第 \(n\) 个位置,计算该位置上的原型与查询样本类别相同的期望值,然后对前 K 个位置求和并取负。将期望展开。对于第 \(n\) 个位置,其损失分量为:
现在,对整个损失函数取极限(当 \(\tau \to 0\),即 \(\widehat{P} \to P\)):
根据 Lemma D.2,当 \(\widehat{P} \to P\) 时,上式变为:
硬排列矩阵 \(P\) 是一个置换矩阵,其每行只有一个元素为 1,其余为 0。因此,对于固定的 \(n\),求和 \(\sum_{m=1}^{N} P[n, m] \cdot \mathbb{I}\left(y^{(m)}=y_{\text{query}}\right)\) 的结果实际上就是:第 \(n\) 个最近邻的原型是否与查询样本同类别。如果是,则该项为 1;如果不是,则为 0。
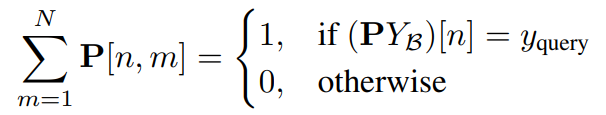
用 \(c_n\) 来表示这个二值结果:
因此,损失函数的极限简化为:
\(\sum_{n=1}^{K} c_n\) 计算的是前K个最近邻中,与查询样本类别相同的原型数量。因此,\(-\sum_{n=1}^{K} c_n\) 就是相同类别原型数量的负值。最小化这个损失,就等价于最大化相同类别原型的数量。反之,也可以理解为最小化不同类别原型的数量。因为前 K 个近邻中,不同类别原型的数量就是 \(K - \sum_{n=1}^{K} c_n\),所以最小化 \(\mathcal{L}_{\text{pred}}\) 直接意味着减少错误近邻的数量,这也就是论文中给出的的形式。
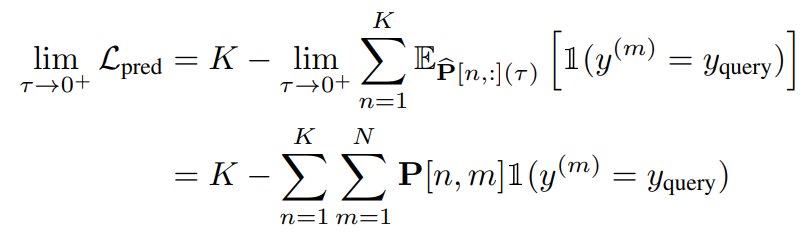


 浙公网安备 33010602011771号
浙公网安备 33010602011771号