Paper Reading: A Survey of Neural Trees: Co-Evolving Neural Networks and Decision Trees
Paper Reading 是从个人角度进行的一些总结分享,受到个人关注点的侧重和实力所限,可能有理解不到位的地方。具体的细节还需要以原文的内容为准,博客中的图表若未另外说明则均来自原文。
| 论文概况 | 详细 |
|---|---|
| 标题 | 《A Survey of Neural Trees: Co-Evolving Neural Networks and Decision Trees》 |
| 作者 | Haoling Li, Jie Song, Mengqi Xue, Haofei Zhang, and Mingli Song |
| 发表期刊 | IEEE Transactions on Neural Networks and Learning Systems |
| 发表年份 | 2024 |
| 期刊等级 | 中国科学院SCI期刊分区(2025年3月最新升级版) 1 区 TOP,CCF-B |
| 论文代码 | https://github.com/JusciAvelino/imbalancedRegression |
作者单位:
- The School of Software Technology and the State Key Laboratory of Blockchain and Security, Zhejiang University, Hangzhou 310013, China.
- Hangzhou High-Tech Zone (Binjiang) Institute of Blockchain and Data Security, Hangzhou 310013, China.
- The School of Computer and Computing Science, Hangzhou City University, Hangzhou 310015, China.
- The College of Computer Science and Technology and the State Key Laboratory of Blockchain and Security, Zhejiang University, Hangzhou 310013, China.
神经树的研究动机
神经网络(NNs)和决策树(DTs)是机器学习中两种流行但范式迥异的模型,它们具有互斥的优势和局限性。神经网络和决策树的优势与局限如下表所示:
| 机器学习模型 | 优势 | 局限 |
|---|---|---|
| 神经网络 | 强大的层次化表示学习能力,能自动学习特征,擅长捕捉复杂非线性关系,泛化能力强,易于并行化。 | 通常被视为“黑箱”模型,决策过程缺乏透明度;训练耗时且计算成本高;架构设计依赖专家知识。 |
| 决策树 | 结构透明,决策路径(从根节点到叶节点的测试序列)清晰可循,具有天生的可解释性;采用数据驱动的贪婪生长法构建,无需预设架构;推理轻量高效。 | 传统轴对齐决策树表达能力有限,分裂策略贪婪且不可微,难以使用梯度下降优化;容易过拟合。 |
现有决策树通过模糊决策树(FDTs) 和斜决策树 等改进,引入了连续性和更复杂的路由函数,为与神经网络的结合提供了理论基础。为了解决两类算法的局限,研究者们探索了将 NNs 和 DTs 结合的方法,统一到 “神经树”(Neural Trees, NTs) 的概念下。NTs 的目标是找到两者优势的“最佳结合点”,本文将 NTs 分为三个主要领域:
- 非混合(Nonhybrid):NNs 和 DTs 作为独立模型协作。例如,用 DTs 为 NNs 提供结构先验,或从训练好的 NNs 中提取 DTs 以进行解释。它们并非一个混合模型。
- 半混合(Semi-Hybrid):NNs 借鉴 DTs 的部分思想(本文主要关注利用类别层次结构),但未在架构中实现决策分支。例如,在损失函数或网络输出中嵌入类别间的层次关系。
- 混合(Hybrid):即神经决策树(Neural Decision Trees, NDTs)。这类模型同时实现了类别层次结构和决策分支,NDTs 利用可微的路由函数,使得整个树结构可以通过梯度下降进行端到端训练。早期的 NDTs 处理低维表格数据,而现代的 NDTs 已能处理图像等复杂数据,但往往需要在性能和可解释性之间进行权衡。
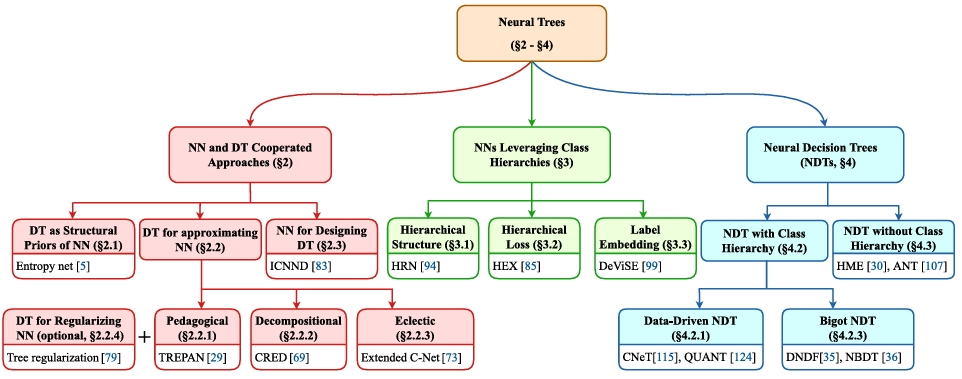
这篇综述的主要焦点是混合方法(NDTs),因为它们被专门设计为具有内在可解释性的模型。核心目标是详细探讨 NTs(尤其是 NDTs)如何增强模型的可解释性,并对它们的性能和面临的挑战进行分析。
非混合:神经网络与决策树协作方法
非混合方法即神经网络和决策树作为独立的模型相互协作,而非融合成一个单一系统。其核心特征是:神经网络和决策树仍然在各自的范式下独立运行,但其中一方被赋予辅助性角色,以帮助另一方更好地完成特定任务(如模型构建、解释或优化)。
决策树作为神经网络的结构先验
这种方法在神经网络(特别是早期)的架构设计中,利用决策树来提供初始的、有意义的模型结构。核心思想是为了解决神经网络对初始权重和架构敏感的问题,利用决策树生成的逻辑描述(规则)来初始化网络连接和权重。代表性工作为熵网络(Entropy Net),方法是将一个轴对齐的决策树映射成一个三层神经网络。其对应关系如下:
- 第一层神经元 ↔ 决策树的内部节点(每个神经元评估一个特征测试)。
- 第二层神经元 ↔ 决策树的叶节点(连接代表从根到该叶子的路径)。
- 输出层神经元 ↔ 类别(指向同一类的路径连接到同一个输出神经元)。
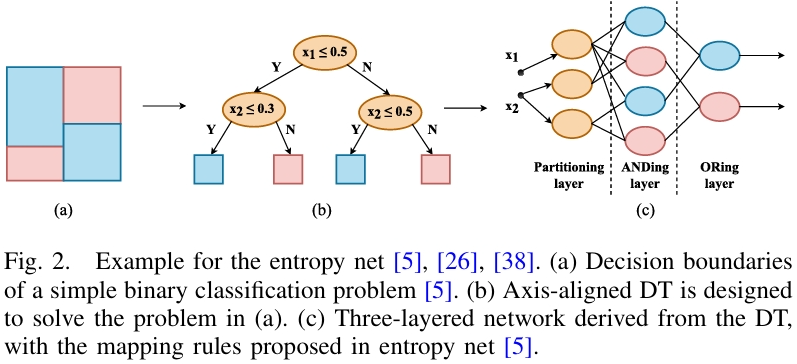
该方法的优势是减少了网络设计的盲目性,生成的网络包含有意义的知识,通常连接更少,并具备决策树缺乏的容错机制。局限在于仅限于使用单一特征分裂,可能导致树结构庞大。后续研究扩展了该方法,支持映射斜决策树,并将输入重新描述为区间隶属函数。近期有研究将类似思想应用于初始化树突神经元模型(DNM),这是一种本身更具可解释性的神经网络。
决策树用于近似/解释神经网络
这类方法的目标是从训练好的神经网络中提取出决策树(或规则集),以解释黑箱模型的决策逻辑。根据提取规则时利用神经网络内部信息的程度,可分为以下几种技术:
- 教学式技术(Pedagogical Techniques):将神经网络视为黑盒,仅利用其输入-输出映射关系。通过向网络查询大量输入(包括真实数据和人工生成数据)对应的输出,然后基于这些输入-输出对来诱导出一个决策树。代表性工作为TREPAN 算法,它使用网络作为“预言机”来标记样本,然后采用类似 ID2-of-3 的算法来生长决策树,并以对网络的保真度(Fidelity)作为分裂标准。优势在于生成的树紧凑、易于理解。局限是保真度可能较低,且难以近似深度神经网络复杂的决策边界。后续有许多改进工作,如简化分裂测试、推广到回归问题等。
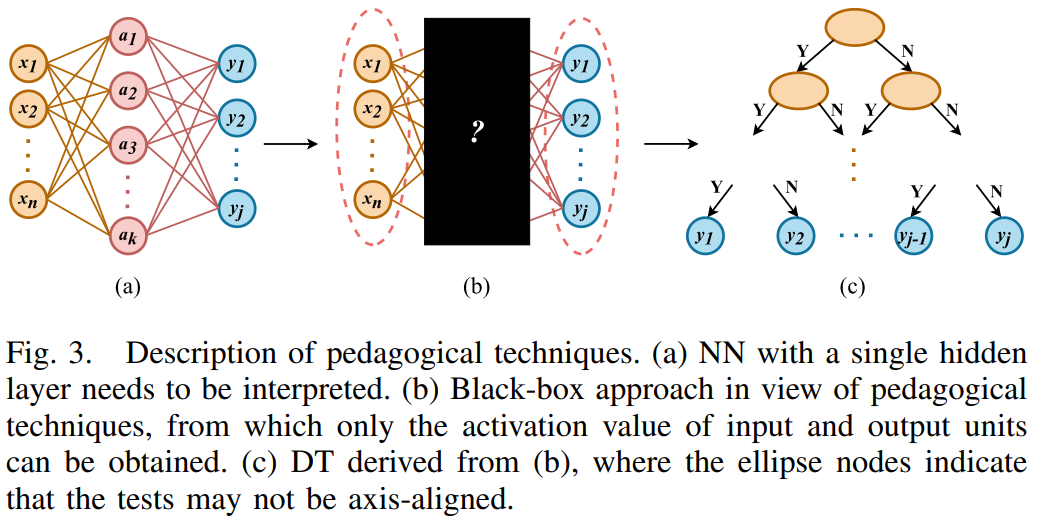
- 分解式技术(Decompositional Techniques):该方法的思想是“打开黑箱”,在单个神经元或连接层面提取规则。为神经网络的每一层甚至每个神经元都诱导决策树,最后将规则合并。优势是保真度最高,能更精确地反映网络的内部机制。局限在于规则数量可能极其庞大,合并后可能难以理解。早期工作限于单隐藏层网络和轴对齐树,后续研究尝试提取斜决策树以更好地匹配网络的决策边界。
- 折中式技术(Eclectic Techniques):结合上述两者,部分利用网络内部信息(如权重大小、隐藏层的贡献矩阵),但不为每个神经元都生成规则。这类方法在保真度和模型简洁性之间取得平衡,例如学习一棵编码卷积神经网络高层特征中所有潜在决策模式的决策树。
- 用于正则化神经网络的决策树:在神经网络训练阶段,引入一个正则化项,鼓励神经网络的决策边界能够被一个简单的决策树很好地近似。这种方法使训练出的网络更容易被后续的规则提取算法解释,但这可能会限制网络的表达能力,从而牺牲一定的准确性。
神经网络用于设计决策树
这种方法与第二种方向相反,神经网络扮演辅助角色,用于提升决策树的质量。其核心思想是利用训练好的神经网络来分析输入特征的重要性(敏感性),过滤掉不相关的特征,然后再用净化后的数据来诱导决策树。类似于知识蒸馏中的“师生”框架,神经网络(老师)告诉决策树(学生)哪些输入特征对于做出正确决策是最重要的。与 ANN-DT 算法的区别在于虽然都进行特征分析,但计算敏感性的方式和应用目标不同。该方法更侧重于为决策树提供更优质的数据预处理。
小结
“非混合”方法无论是 DT→NN 的映射还是 NN→DT 的近似,其核心目标都是实现两种模型在功能上的一致性甚至等价性。因为决策树是对复杂模型的近似,所以提取出的决策树性能通常无法完全匹配其神经网络原型。这些方法属于事后解释(Post-hoc Explanation),旨在解释已经训练好的黑箱模型,而非设计本身就可解释的模型。其可信度依赖于近似的质量。同时,这些方法也展示了 NNs 和 DTs 之间可以相互支持,形成协同效应,从而在多样化的任务中产生更稳健和全面的预测。
半混合:利用类别层次结构的神经网络
在决策树中,从根节点到叶节点的路径天然地形成了一个标签树(label tree),每个内部节点代表一个泛化的大类(超类),其子节点代表更具体的子类。这种层次结构可以是基于领域知识预先定义的,也可以由算法自动生成。半混合的方法中,神经网络部分借鉴决策树思想的模型,具体而言是吸收了决策树所蕴含的“类别层次结构”思想。这类的神经网络隐式地将标签树编码到网络之中,但由于其架构中缺乏决策分支,因此无法像决策树那样实现逐步推理。它们只是利用了类别间的层次关系来改进模型。
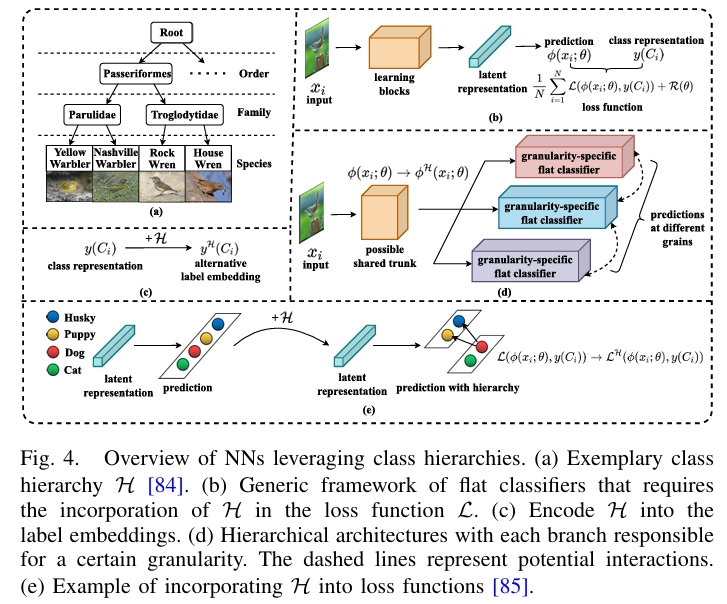
为了统一理解这些方法,论文引用了一个通过最小化损失函数来学习预测函数的扁平分类器作为通用框架,这是一个标准的机器学习模型经验风险最小化目标,公式及其符号含义如下表所示。该框架本身对类别层次结构 \(\mathcal{H}\) 是不可知的,半混合方法的核心就是通过修改 \(\phi\)(层次化架构)、\(\mathcal{L}\)(层次化损失函数)或 \(y\)(标签嵌入)来融入 \(\mathcal{H}\)。
| 符号 | 说明 |
|---|---|
| \(\phi\left(x_{i} ; \theta\right)\) | \(\theta\) 的预测函数(如神经网络)对样本 \(x_i\) 的输出 |
| \(y(C_i)\) | 类别标签 \(C_i\) 的某种嵌入表示v |
| \(\mathcal{L}\) | 损失函数,用于比较预测输出与真实标签。 |
| \(\mathcal{R}(\theta)\) | 正则化项,防止过拟合 |
层次化架构
层次化架构方法将网络设计成分支结构,每个分支负责识别类别层次中某一特定粒度级别的概念。与决策树的根本区别在于每个分支都是一个扁平分类器,接收全部数据并进行预测,而决策树的每个节点只处理经父节点划分后的部分数据。这类方法大致包括:
- 早期方法为层次结构中的每一级单独训练一个多层感知机(MLP),并将上一级的预测结果作为下一级的输入;
- 共享主干方法使用一个共享的神经网络主干(如 CNN),然后在不同层或同一层后连接多个分支(如全连接层),每个分支输出对应粒度级别的预测;
- 近期研究更注重不同分支间的交互。例如,学习层次间的标签转移矩阵来编码相关性,或使用层次残差网络(HRN)将粗粒度特征作为残差连接到细粒度特征上。
层次化损失函数
层次化损失函数方法的网络本身是扁平的,但损失函数被设计得能够利用标签树的层次关系,从而迫使网络的输出概率与 \(\mathcal{H}\) 定义的约束相一致。策略是对语义上距离真实类别较远的错误预测施加更大的惩罚。因为它允许一个扁平网络完成层次分类任务,所以相比层次化架构,该方法优势在于参数更少,计算更高效。代表性工作有:
- HEX图:将类别层次编码为一个有向无环图(DAG),并在其上定义损失函数,确保输出概率符合层次语义约束。
- 层次交叉熵:将分类器的输出沿标签树路径分解为一系列条件概率,并将损失定义为这些条件概率交叉熵的加权和。
层次化标签嵌入
层次化标签嵌入方法将类别层次结构 \(\mathcal{H}\) 编码到标签的向量表示(嵌入) 中,使得嵌入空间中的相对位置或相互关系能够反映类别间的语义相似性。代表性工作为DeViSE 模型,它将图像特征和来自文本(如 Wikipedia)的类别语义嵌入映射到同一空间,通过比较相似度进行分类。这类方法特别适用于零样本学习,即识别在训练集中未出现过的类别。模型学习一个兼容性函数,为图像和其正确类别的嵌入赋予高分数。通过引入外部语义信息,增强了模型的泛化能力和语义合理性。
小结
半混合方法通过利用类别层次结构中的相关性,使得额外的语义信息与原始视觉概念相结合,能增强深度模型的整体性能。错误分类的样本更可能被分到语义相关的类别中,从而减轻了严重误判的后果。局限在于由于缺乏决策分支,这些模型无法进行逐步推理,因此对于提升模型的可解释性贡献有限。它们无法像决策树或后续将介绍的神经决策树(NDTs)那样,提供一个清晰的、步骤化的决策路径。
混合:神经决策树
神经决策树 NDTs 是神经网络与决策树完全融合的产物,其核心理念是构建一个兼具神经网络强大表示学习能力和决策树透明推理过程的混合模型。与事后解释黑箱模型的“非混合”方法不同,NDTs 设计初衷就是内在可解释的。其关键创新在于利用可微的神经网络组件来实现决策树中的路由函数,从而使得整个树结构可以通过梯度下降进行端到端的全局优化,克服了传统决策树贪心、不可微的缺点。NDTs 可根据是否实现类别层次结构进行分类:
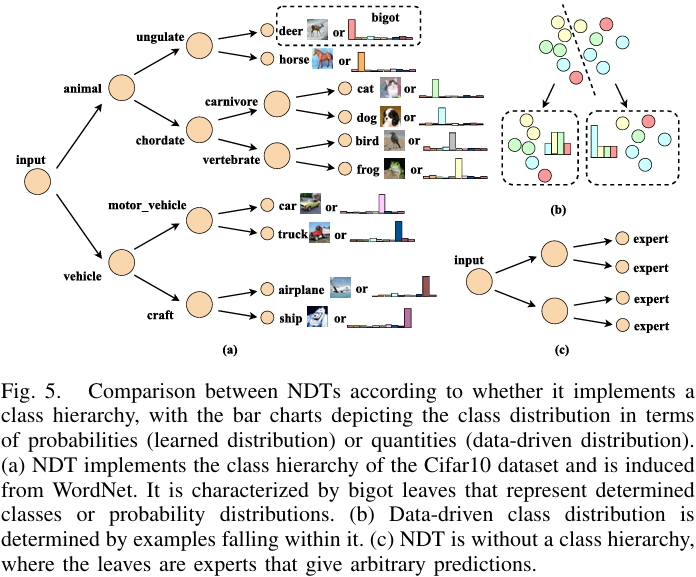
- 具有类别层次的 NDTs:每个内部节点代表一个具体的概念(超类),叶节点对应具体的类或确定的分布。模型通过清晰的、层次化的决策路径进行推理,可解释性强。
- 无类别层次的 NDTs(专家 NDTs):叶节点是灵活的“专家”分类器,可为任意输入预测任意的类别分布。性能更强,但可解释性较弱。
NDTs 的通用组成与推理机制
一个通用的 NDT 可以分解为三个基本模块,其拓扑结构定义为 $T:={\mathcal{N},\mathcal{E}} $,即节点集和边集:
| NDTs 组件 | 说明 | 功能 |
|---|---|---|
| 路由器 | 每个内部节点配备一个路由器 \(r_{i}^{\theta}\),通常是一个小型神经网络,如线性层或 MLP | 接收输入,输出一个概率分布,决定数据应流向哪个子节点。这是实现可微决策的核心。 |
| 学习器(可选) | 位于边上 $ l_{i}^{\psi} $ | 负责在数据沿树向下传递时对其进行特征变换(表示学习)。多数 NDTs 为简化起见,使用恒等函数,即数据本身不发生变化。 |
| 求解器 | 每个叶节点配备一个求解器 $ s_{i}^{\phi} $ | 负责给出最终预测,其设计是区分 NDTs 类型的关键。 |
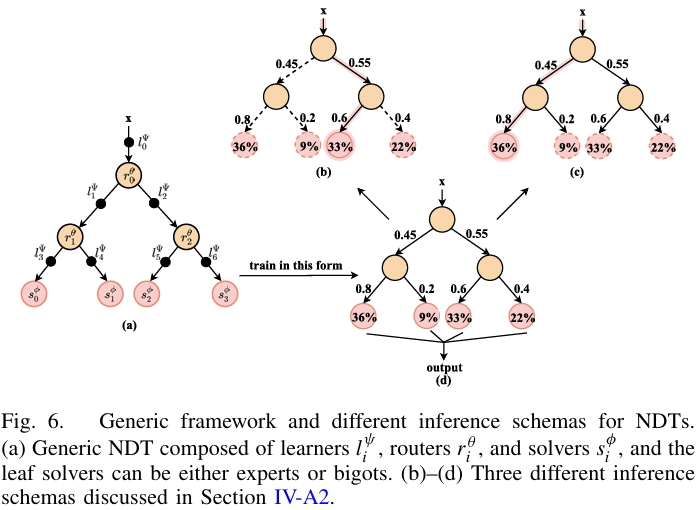
求解器大致可以分为两类:
| 求解器类型 | 说明 |
|---|---|
| Bigot Leaves(固执叶) | 输出一个静态的、确定的类别分布,通常是 one-hot 或近似 one-hot。这强制实现了类别层次,可解释性高。 |
| Expert Leaves(专家叶) | 输出一个依赖于输入的、任意的类别分布,如一个线性分类器。这类灵活性高,性能好,但可解释性弱。 |
NDTs 支持三种推理模式,在训练和测试阶段可根据需求选择:
| NDTs 推理模式 | 说明 | 特点 |
|---|---|---|
| 软推理 | 输入以概率形式同时到达所有叶节点,最终预测是所有叶节点预测的加权平均 | 支持并行计算,精度高,但解释整个树较复杂 |
| 全局贪心推理 | 选择到达概率最高的那个叶节点的预测作为最终结果 | 比软推理更具可解释性 |
| 硬推理 | 在每个内部节点都选择概率最高的分支,形成一条单一的决策路径 | 计算成本最低,可解释性最强,但可能因局部最优而牺牲精度 |
其中软推理的公式如下,\(p(R=l \mid x, \psi, \theta)\) 是样本 \(x\) 到达第 \(l\) 个叶节点的路径概率,由路由器的参数 \(\theta\) 和 \(\psi\) 决定。\(p(\hat{y} \mid x, R=l, \phi, \psi)\) 是第 \(l\) 个叶节点求解器给出的预测分布。最终预测是所有叶节点预测的概率加权平均,确保了模型的可微性,支持端到端的梯度训练。
计算从根节点到某个叶节点 \(l\) 的路径概率 \(\pi_{l}\) 的公式及符号含义如下所示,
| 符号 | 说明 |
|---|---|
| \(\mathcal{P}_{l}\) | 从根节点到叶节点 \(l\) 的唯一路径 |
| \(\prod\) | 表示路径概率是路径上所有路由器决策概率的连乘积 |
| \(\left(r_{i}^{\theta}\left(x_{i}^{\psi}\right)\right)_{j}\) | 路径上第 \(i\) 个路由器将数据路由到其第 \(j\) 个子节点的概率 |
| \(\mathbb{I}\left(C(i)_{j} \in \mathcal{P}_{l}\right)\) | 指示函数,当且仅当第 \(j\) 个子节点也在路径 \(\mathcal{P}_{l}\) 上时值为 1,否则为 0 |
具有类别层次的 NDTs
这类 NDTs 可进一步分为数据驱动、固执型两种构建方式。数据驱动的 NDTs模仿传统决策树,基于数据依赖的启发式方法(如信息增益、基尼不纯度)来生长树结构。叶节点的标签由落入该叶节点的训练样本的分布决定。代表性工作为在内部节点训练小型神经网络作为路由器,以最大化类别纯度或信息增益。一些方法也应用于模糊 NDTs,通过全局优化模糊分裂的参数。优势是支持增量学习,但局限性在于基于样本分布的标签可能无法很好地捕捉数据底层模式,性能通常较差。
固执型 NDTs 的树结构是预先定义好的,并进行全局优化。叶节点的分布是学习到的(但通常是静态的),并且是 one-hot 或近似 one-hot 的,从而隐式地诱导出类别层次。这类方法的优势是可解释性强,局限是叶节点的强约束(必须是确定的分布)限制了模型的表达能力,通常会导致性能下降。
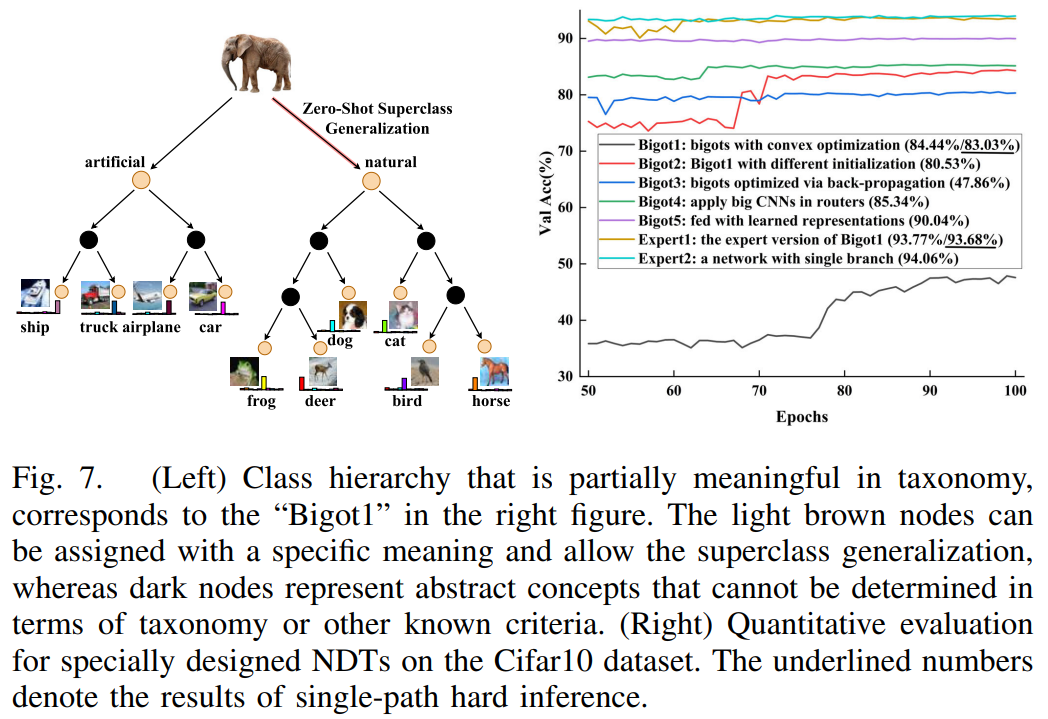
固执型 NDTs 的代表性工作有:
- Deep Neural Decision Forests (DNDFs):使用 CNN backbone 学习特征,其最后一层作为树的路由器。叶节点的分布通过一个独立的凸优化问题求解,不与网络参数共同训练。
- Neural-Backed Decision Trees (NBDTs):利用外部知识库(如 WordNet)为每个节点分配语义概念,支持零样本超类泛化。
- ProtoTree:将原型集成到每个节点中。决策基于输入图像中是否存在这些可解释的原型部分做出,极大地增强了路由过程的透明度。
无类别层次的 NDTs(专家 NDTs)
无类别层次的 NDTs 的叶节点是“专家”分类器,可以给出任意预测。模型缺乏明确的类别层次,但获得了极大的灵活性。代表性工作是 层次专家混合模型(HME),它采用树结构但每个叶节点是一个回归或分类模型,模型通过期望最大化(EM)算法学习。现代变体有将 HME 与 CNN、注意力机制甚至 Transformer 结合,以处理图像等复杂数据。这类方法通常能获得更高的性能,更接近标准DNNs。局限性在于节点的任务不明确,决策路径的意义模糊,导致可解释性大幅降低。
小结
神经决策树的核心在于通过可微路由将决策树的结构与神经网络的优化能力相结合,其设计始终围绕性能与可解释性之间的权衡。具有类别层次的NDTs(特别是固执 NDTs),使用硬推理输入原始数据,它具有更好的可解释性,但这会严重限制性能。专家 NDTs 使用软推理,输入由另一个 NN 提取的隐式特征,这类方法通常性能更好,但这会牺牲从输入到输出的端到端可解释性。NDTs 的关键挑战在于如何在不显著牺牲性能的前提下,设计出具有高透明度和可分解性的模型。
分析与展望
评估模型可解释性有两个关键标准:
- 可分解性:模型能否被分解为功能明确、可独立理解的组件(如决策树的节点和路径)。决策树是高度可分解的,而典型的神经网络则不然。
- 透明度:模型的决策过程是否清晰可循、易于理解(如决策树基于信息增益的分裂规则)。神经网络的参数编码决策逻辑,缺乏透明度。
基于此可以将神经树技术分为事后解释、事前可解释建模两大解释范式。事后解释主要为 NN 近似方法,它们为已训练好的黑盒神经网络构建一个可解释的代理模型(如决策树)。基本逻辑是通过提取规则来近似神经网络学习到的决策边界,并推测其决策原因。优势是模型无关,适用于任何现有或未来的黑盒模型。局限在于简单的代理模型(如决策树)难以完全复现复杂神经网络的非线性决策边界,导致解释可能不准确,保真度不足。另一方面由于是近似,无法保证解释的绝对正确性,存在可信度不高的问题。原文引用建议在高风险决策中停止解释黑箱模型,转而直接使用可解释模型。未来建议使用更强大但仍可解释的代理模型(如 NDTs 本身),以减少准确性的损失。
事前可解释建模主要为 神经决策树(NDTs),这些模型本身就被设计成可解释的。本文在不同组件的设计方面的总结如下:
- 路由器:大多数 NDTs 使用小型神经网络作为路由器,这虽然实现了可分解性(每个节点功能明确),但路由器本身是一个“小黑箱”,缺乏透明度。ProtoTree等工作是未来方向,它们通过原型(Prototypes) 等机制为路由决策提供了直观的理由,显著提升了透明度。
- 叶节点求解器:专家叶节点使用灵活的分类器,性能好但破坏了类别层次,导致模型可解释性弱。固执叶节点:输出确定的类别分布,强制形成类别层次,可解释性强,但强约束导致性能下降。实验表明,通过反向传播联合优化固执叶节点效果很差,而采用独立凸优化则更稳定但性能仍有瓶颈。有论文提出“具有类别偏好的专家” 作为未来方向。,对专家叶节点的权重施加稀疏性或负相关性约束,使其“偏爱”某个或某几个类别,从而隐式地诱导出类别层次,在保持性能的同时提升可解释性。
- 树结构的形成:数据驱动 NDTs 的可分解性和潜在透明度最高,但性能通常不如全局优化的神经网络式 NDTs,近年来研究较少。未来倾向于研究如何对预设的神经网络式树结构进行更好的优化和解释。
- 输入表示:输入原始数据:可实现从输入到输出的端到端完整解释,但 NDTs 需同时进行特征学习和决策,任务艰巨,性能较低。输入隐式特征将 NDT 作为预训练神经网络顶部的“解释头”,性能可接近骨干网络,但解释范围仅限于特征空间,无法追溯到原始输入,是用解释范围换取性能。
在决策树启发的神经网络方面,本文也梳理了未被纳入主分类的、具有分支结构的神经网络。它们虽能实现条件计算(动态路由),但其复杂的拓扑结构(如 DAG)和组件黑箱性限制了其可解释性,与专家 NDTs 更为相似。在推理效率方面,软推理便于并行但计算成本高;硬推理(单路径)可实现条件计算,节省资源,但不利于并行。建议未来探索利用随机神经元等技术,在训练中实现分支的随机失活,以兼顾两者。
理想的、兼具高性能与高可解释性的 NDTs 仍面临挑战,未来的研究应致力于打破或优化性能与可解释性之间的权衡。论文最终提出了三个最具潜力的发展方向:
- 具有类别偏好的专家 NDTs:通过约束软化固执叶节点,在保持性能的同时诱导层次结构。
- 透明路由机制:推广类似 ProtoTree 的原型概念,使路由决策变得直观可信。
- 逐步推理的网络反卷积:对于处理原始数据的 NDTs,在中间决策层引入可解释的特征,提升逐步推理的可靠性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号