[bzoj4417] [洛谷P3990] [Shoi2013] 超级跳马

Description###

现有一个n行m列的棋盘，一只马欲从棋盘的左上角跳到右下角。每一步它向右跳奇数列，且跳到本行或相邻行。跳越期间，马不能离开棋盘。例如，当n = 3, m = 10时，下图是一种可行的跳法。

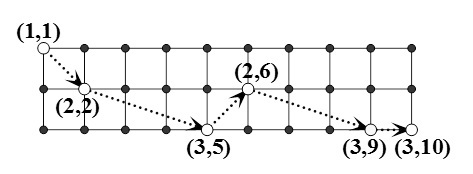
试求跳法种数mod 30011。

Input###

仅有一行，包含两个正整数n, m，表示棋盘的规模。

Output###

仅有一行，包含一个整数，即跳法种数mod 30011。

Sample Input###

3 5

Sample Output###

10

HINT###

对于100%的数据，1 ≤ n ≤ 50，2 ≤ m ≤ 10^9

---

想法##

其实就是矩阵随便转移一下就出来了。。。
分奇偶列考虑，记录每行奇数列及偶数列的sum

像我这么lazy的人，就直接一列列转移了。。。
转移矩阵：

\[\begin{bmatrix} 0&0&0&…&0&1&0&0&…&0\\ 0&0&0&…&0&0&1&0&…&0 \\ 0&0&0&…&0&0&0&1&…&0 \\ …&&&&&…&&&&\\ 0&0&0&…&0&0&0&0&…&1 \\ 1&0&0&…&0&1&1&0&…&0 \\ 0&1&0&…&0&1&1&1&…&0 \\ 0&0&1&…&0&0&1&1&…&0 \\ …&&&&&…&&&&\\ 0&0&0&…&1&0&0&0&…&1 \\ \end{bmatrix} \quad \]

---

代码##

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

#define P 30011

using namespace std;

const int SZ = 105;

int n,m;

struct matrix{
    int a[SZ][SZ];
    matrix() { memset(a,0,sizeof(a)); }
    void init() { for(int i=0;i<SZ;i++) a[i][i]=1; }
    matrix operator * (const matrix &b) const{
        matrix c;
        for(int i=0;i<n*2;i++)
            for(int j=0;j<n*2;j++)
                for(int k=0;k<n*2;k++)
                    (c.a[i][j]+=a[i][k]*b.a[k][j])%=P;
        return c;	
    }
    matrix operator *= (const matrix &b) { return *this=*this*b; }
};
matrix Pow_mod(matrix x,int y){
    matrix ret; ret.init();
    while(y){
        if(y&1) ret*=x;
        x*=x;
        y>>=1;	
    }
    return ret;
}

int main()
{
    scanf("%d%d",&n,&m);
    
    int ans;
    matrix a,b;
    for(int i=0;i<n;i++) 
        a.a[i+n][i]=a.a[i][n+i]=1;
    for(int i=1;i<n-1;i++)
        a.a[i+n][i+n]=a.a[i-1+n][i+n]=a.a[i+1+n][i+n]=1;
    a.a[n][n]=a.a[2*n-1][2*n-1]=1; 
    if(n!=1) a.a[n+1][n]=a.a[2*n-2][2*n-1]=1;
    
    b.a[0][0]=b.a[0][n]=b.a[0][n+1]=1;
    if(m==2) { printf("%d\n",b.a[0][2*n-1]); return 0; }
    
    b=b*(Pow_mod(a,m-3));
    ans=b.a[0][n-1];
    b*=a;
    ans=(b.a[0][n*2-1]-ans+P)%P;
    printf("%d\n",ans);
    
    return 0;
}