数位DP详细解析
1.定义与原理

2.例题一:
题目
思路
我们做数位 \(DP\) 时,一般有如下两个技巧方便做题,理清思路:
-
1.对于求一段数中满足条件的数的个数,可以用前缀和的方法完成,即 $ans=dp (r)-dp(l-1) $;
-
2.在想思路时,可以把问题转换成 树 的形式,对每个步骤分情况讨论,下面拿这道题来举例子:
首先分析样例,把 \(15\) 到 \(20\) 中的所有数转化为二进制:
\(15=1111,16=10000,17=10001,18=10010,19=10011,20=10100\)
总结规律,得出结论,问题转化为:从 \(l\) 到 \(r\) 中所有数的 \(b\) 进制中恰好有 \(k\) 个 \(1\) 的数的个数。
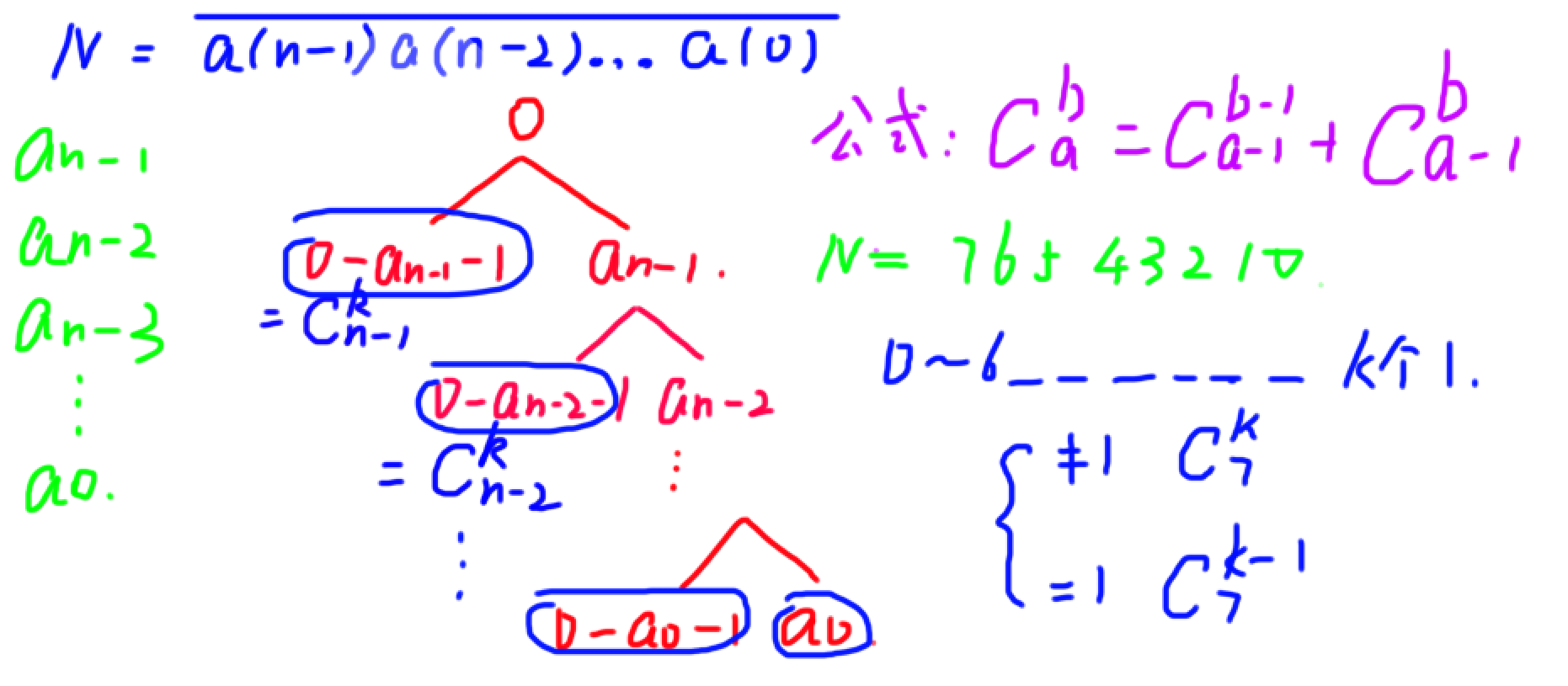
那么我们结合这张图具体分析:
我们令一个 \(N\) 位数,其每一位为 \(a_{(n-1)},a_{(n-2)}...a_{0}\),然后我们把每一位竖着写好,在从高到低对每一位分情况讨论。
比如我们对 \(a_{(n-1)}\) 讨论,因为这是个 \(N\) 进制数,所以其每一位都小于 \(N\)。
然后我们分出两种情况:小于 \(a_{(n-1)}\) 和等于 \(a_{(n-1)}\)。
比如这个数为 \(76543210\),我们取第一位时可以取 \(0\) 到 \(6\) 之间的任何数,也可以取 \(7\)。
-
1.当取 \(0\) 到 \(6\) 时,又分为取非 \(1\) 和取 \(1\) 两种情况。当取的数不是 \(1\) 时,意味着我们将在剩下的 \(N-1\) 个数中填 \(k\) 个 \(1\),总方案数为 \(C_{N-1}^{k}\);否则,说明已经填入了一个 \(1\),总方案数为 \(C_{N-1}^{k-1}\)。
-
2.当取的数为 \(7\) 时,说明这一位已经被固定,于是我们继续用同样思路推下一位即可。
最后,当我们推到 \(a_0\) 时,同样分两种情况,但此时已经不能再往下分支了,所以最后的答案就是图中所有左边的分支和 \(a_0\) 这一块。
代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
// #define int long long
using namespace std;
#define N 1010
#define For(i,j,k) for(int i=j;i<=k;i++)
#define IOS ios::sync_with_stdio(0),cin.tie(),cout.tie()
int l, r, k, b;
int c[N][N];
void init () {
For (i, 0, N - 1) {
For (j, 0, i) {
if (j == 0) c[i][j] = 1;
else c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
}
} //初始化组合数
}
int dp (int n) {
if (n == 0) return 0; //特判边界
vector <int> nums;
while (n) nums.push_back (n % b), n /= b; //将n转化成b进制数
int res = 0, lst = 0; //前面是模板
//res是答案,lst是计算右分支时的前缀信息(已经填好的数中1的个数)
for (int i = nums.size () - 1; i >= 0; i --) { //倒序循环,因为进制转换时存的数是倒序的
int x = nums[i];
if (x) { //只有x>0时才有左右分支
res += c[i][k - lst]; //首先肯定可以填0,,就在剩下i位中填k-lst个数
if (x > 1) { //如果可以取1,那就假设取的就是1
if (k - lst - 1 >= 0) res += c[i][k - lst - 1];
//还需取1的个数减1,记得判断一下是否还能再取
//因为对于右边分支取的就是x本身(x>1),所以不合法,直接break!
break;
} else { //当x==1时,只能取0,所以交给下一位,下一位可使用的1的个数会少1,体现在代码上是last+1
lst ++;
if (lst > k) break; //如果已经填了k个1,就退出
}
}
if (i == 0 && lst == k) { //最右侧分支上的方案
res ++;
} //如果算到最后一位且已经填了k个1,就退出
}
// cout << endl;
return res;
}
int main () {
IOS;
init ();
cin >> l >> r >> k >> b;
cout << dp (r) - dp (l - 1) << endl; //前缀和思想
return 0;
}
3.例题2:数字游戏
题目
思路
思路和上题一样,只是我们在处理左边分支时方法不一样。
本题让我们求 \(1\) 到 \(n\) 中的不降数。我们不妨用 \(f[i][j]\) 表示以 \(j\) 为最高位的 \(i\) 位数中有多少种取值方案。
我们发现,当最高位取值为 \(j\) 时,其下一位是从 \(j\) 到 \(9\) 中的任意数字。如果下一位确定了,我们就把第 \(i\) 位抹掉,继续往下走。
所以,预处理的状态转移方程为 \(f[i][j] = f[i][j]+f[i-1][k] (k>=j)\)
然后在数位 \(DP\) 的过程中,我们首先加上左分支的方案数。为了保证不降序,我们从上一位 \(lst\) 开始枚举,当选完这一位数后,剩下要填的数的个数为 \(i-0+1\) 个,所以每次答案加上 $f[i+1][j] $
然后判断,如果已经出现了降序,就退出,最后处理一下右边分支即可。
代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
//#define int long long
using namespace std;
#define N 15
#define For(i,j,k) for(int i=j;i<=k;i++)
#define IOS ios::sync_with_stdio(0),cin.tie(),cout.tie()
int a, b, f[N][N];
//f[i][j]表示以j为最高位的i位数的数的个数
void init () {
For (i, 0, 9) f[1][i] = 1;
For (i, 2, N - 1)
For (j, 0, 9)
For (k, j, 9)
f[i][j] += f[i - 1][k];
}
int dp (int n) {
if (n == 0) return 1;
vector <int> nums;
while (n) nums.push_back (n % 10), n /= 10;
int res = 0, lst = 0;
//----------------------------
for (int i = nums.size () - 1; i >= 0; i --) {
int x = nums[i];
For (j, lst, x - 1)
res += f[i + 1][j];
if (x < lst) break;
lst = x;
if (i == 0) res ++;
}
return res;
}
int main () {
IOS;
init ();
while (cin >> a >> b) {
cout << dp (b) - dp (a - 1) << endl;
}
return 0;
}
4.例题3:Windy数
题目
思路
还是一样的在预处理时很容易推出公式:在满足相邻两位之差至少为 \(2\) 时,有公式 \(f[i][j] += f[i - 1][k]\)
然后分别处理左边分支和右边分支:
-
1.左边:首先要特判一下,如果是最高位就从1开始枚举,否则从0开始枚举;然后枚举到当前位减1,每次判断如果合法,就将答案加上 \(f[i + 1][j]\)
-
2.右边:首先判断能不能往下做分支,就是说当前位是否比上一位至少大2。如果是的话,就将 \(lst\) 更新,否则说明没有分支,直接退出循环。
然后如果已经算到最后一位,就将答案加1即可。
最后,因为这个数不能带前导 \(0\),还要再处理一遍带前导 \(0\) 的数。
代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
//#define int long long
using namespace std;
#define N 15
#define For(i,j,k) for(int i=j;i<=k;i++)
#define IOS ios::sync_with_stdio(0),cin.tie(),cout.tie()
int a, b, f[N][N];
//f[i][j]表示以j为最高位的i位数的数的个数
void init () {
For (i, 0, 9) f[1][i] = 1;
For (i, 2, N - 1)
For (j, 0, 9)
For (k, 0, 9)
if (abs (j - k) >= 2)
f[i][j] += f[i - 1][k];
return ;
}
int dp (int n) {
if (n == 0) return 0;
vector <int> nums;
while (n) nums.push_back (n % 10), n /= 10;
int res = 0, lst = -2; //lst记录上一位数字,初始值需比0~9的任意数字之差>=2
//----------------------------
for (int i = nums.size () - 1; i >= 0; i --) {
int x = nums[i];
for (int j = i == nums.size () - 1; j < x; j ++)
if (abs (j - lst) >= 2)
res += f[i + 1][j];
if (abs (x - lst) >= 2) lst = x;
else break;
if (i == 0) res ++;
}
//特殊处理有前导0的数
For (i, 1, nums.size () - 1)
For (j, 1, 9)
res += f[i][j];
return res;
}
int main () {
IOS;
init ();
cin >> a >> b;
cout << dp (b) - dp (a - 1) << endl;
return 0;
}
5.例题4:数字游戏II
题目
思路
还是一样的思路,我们着重讲预处理的方法:
我们用 \(f[i][j][k]\) 表示所有以 \(j\) 为最高位的所有数字和能整除 \(k\) 的 \(i\) 位数的数量。
每当我们取下一位时,假如我们取的数为 \(x\),那么位数少1,最高位为 \(x\),其数字和取余后余数为 \((k-j) mod p\)。
所以状态转移方程为 \(f[i][j][k] += f[i - 1][x][mod (k - j, p)];\)。
然后数位 \(DP\) 的过程还是差不多,稍微变通一下就可以了。
代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
//#define int long long
using namespace std;
#define N 15
#define For(i,j,k) for(int i=j;i<=k;i++)
#define IOS ios::sync_with_stdio(0),cin.tie(),cout.tie()
int a, b, p, f[N][N][110];
//f[i][j]表示以j为最高位的i位数的数的个数
int mod (int x, int y) {
return (x % y + y) % y;
}//得到整数余数
void init () {
For (i, 0, 9) f[1][i][i % p] ++;
for (int i = 2; i < N; i ++)
for (int j = 0; j <= 9; j ++)
for (int k = 0; k < p; k ++)
for (int x = 0; x <= 9; x ++)
f[i][j][k] += f[i - 1][x][mod (k - j, p)];
}
int dp (int n) {
if (n == 0) return 1;
vector <int> nums;
while (n) nums.push_back (n % 10), n /= 10;
int res = 0, lst = 0; //lst记录前面所有数字之和
//----------------------------
for (int i = nums.size () - 1; i >= 0; i --) {
int x = nums[i];
for (int j = 0; j < x; j ++)
res += f[i + 1][j][mod (-lst, p)];
//第三维解释:因为前面数之和(lst)加上后面数之和 mod p=0,所以后面数之和为 (-lst mod p)
lst += x;
if (i == 0 && lst % p == 0) res ++;
}
return res;
}
int main () {
IOS;
while (cin >> a >> b >> p) {
init ();
cout << dp (b) - dp (a - 1) << endl;
}
return 0;
}
6.例题5:不要62
题目
思路
我们用 \(f[i][j]\) 表示以 \(j\) 为最高位的 \(i\) 位数的满足条件的数的个数。首先常规操作处理完一位数后,对于每个满足条件的方案,有公式 \(f[i][j] += f[i - 1][k]\)
然后再正常跑一遍数位 \(DP\) 即可。
需要注意的就是需要随时判断一下当前位是否为 \(4\),或当前位与上一位是否为 \(62\)。
代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
//#define int long long
using namespace std;
#define N 110
#define For(i,j,k) for(int i=j;i<=k;i++)
#define IOS ios::sync_with_stdio(0),cin.tie(),cout.tie()
int l, r, f[N][N];
//f[i][j]表示以j为最高位的i位数的满足条件的数的个数
void init () {
for (int i = 0; i <= 9; i ++)
if (i != 4)
f[1][i] = 1;
for (int i = 2; i < N; i ++) {
for (int j = 0; j <= 9; j ++) {
if (j == 4) continue;
for (int k = 0; k <= 9; k ++) {
if (k == 4 || (j == 6 && k == 2)) continue;
f[i][j] += f[i - 1][k];
}
}
}
}
int dp (int n) {
if (!n) return 1;
vector <int> nums;
while (n) nums.push_back (n % 10), n /= 10;
int res = 0, lst = 0; //lst记录上一位的数值,只要不为6即可,用于判断是否组成62
//----------------------------
for (int i = nums.size () - 1; i >= 0; i --) {
int x = nums[i];
for (int j = 0; j < x; j ++) {
if (j == 4 || (lst == 6 && j == 2)) continue;
res += f[i + 1][j];
}
if (x == 4 || (lst == 6 && x == 2)) break;
lst = x;
if (!i) res ++;
}
return res;
}
int main () {
IOS;
init ();
while (cin >> l >> r, l || r) {
cout << dp (r) - dp (l - 1) << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号