7.6.0 头文件
import torch
from torch import nn
from d2l import torch as d2l
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
torch.set_printoptions(threshold=np.inf)
7.6.1 批量归一化层
# 定义批量归一化层的前向传播函数,把输入特征X进行归一化
# X:输入特征集合
# gamma:拉伸系数
# beta:偏置系数
# moving_mean:全局均值
# moving_var:全局方差
# eps:极小值
# momentum:一个批量的样本对全局样本的影响系数
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 测试模式走这里
# 如果是在预测模式下,直接利用训练时得到的全局均值和全局方差对输入特征集合进行标准化
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
# 训练模式走这里
assert len(X.shape) in (2, 4) #(如果既不是全连接层也不是卷积层,就报错)
# 如果是全连接层(全连接层第一维是批量大小,第二维是特征量)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0) # 对所有样本的每个特征各计算一次平均值
var = ((X - mean) ** 2).mean(dim=0) # 对所有样本的每个特征各计算一次方差
else:
mean = X.mean(dim=(0, 2, 3), keepdim=True) # 对属于某个通道的所有数计算平均值(包括所有样本,以及这个通道中的所有行和所有列)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True) # 对属于某个通道的所有数计算方差(包括所有样本,以及这个通道中的所有行和所有列)
# 利用均值和方差将输入特征集合X进行标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新整个训练集输入特征的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
# 利用标准化后的特征集合X以及缩放系数和偏置系数,得到标准化之后的特征集合Y,作为批量归一化层的输出
Y = gamma * X_hat + beta
return Y, moving_mean.data, moving_var.data
# 定义批量归一化层
class BatchNorm(nn.Module):
# um_features:用在全连接层后面等同于全连接层的输出个数,用在卷积层后面等同于卷积层的输出通道数
# num_dims:为2表示完全连接层,为4表示卷积层
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
# 如果用在全连接层后面
shape = (1, num_features) # (1,全连接层的输出个数)
else:
shape = (1, num_features, 1, 1) # (1,卷积层的输出通道数,1,1)
# 将拉伸系数初始化为全1
self.gamma = nn.Parameter(torch.ones(shape))
# 将偏置系数初始化为全0
self.beta = nn.Parameter(torch.zeros(shape))
# 全局均值初始化为全0
self.moving_mean = torch.zeros(shape)
# 全局方差初始化为全1
self.moving_var = torch.ones(shape)
def forward(self, X):
# 将X与moving_mean和moving_var复制到显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var
# 计算输入特征集合X的标准化结果Y,全局均值moving_mean、全局方差moving_var
Y, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean,self.moving_var, eps=1e-5, momentum=0.9)
return Y
7.6.2 网络模型
net = nn.Sequential(
# 卷积核尺寸为6×6的卷积层、批量归一化层、Sigmoid激活函数层
nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
# 尺寸为2×2的平均池化层
nn.AvgPool2d(kernel_size=2, stride=2),
# 卷积核尺寸为5×5的卷积层、批量归一化层、Sigmoid激活函数层
nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
# 尺寸为2×2的平均池化层、展平层
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
# 全连接隐藏层、批量归一化层、Sigmoid激活函数层
nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
# 全连接隐藏层、批量归一化层、Sigmoid激活函数层
nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
# 全连接输出层
nn.Linear(84, 10))
7.6.3 训练过程
# 定义学习率、训练轮数、批量大小
lr, num_epochs, batch_size = 1.0, 10, 256
# 下载fashion_mnist,并对数据集进行打乱和按批量大小进行切割的操作,得到可迭代的训练集和测试集(训练集和测试集的形式都为(特征数据集合,数字标签集合)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 使用GPU对模型进行训练,输出最后一轮训练时的平均损失、在训练集上的平均准确率、在测试集上的平均准测率,输出每秒能够训练多少张图像
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# 输出:
# loss 0.264, train acc 0.903, test acc 0.739
# 18366.4 examples/sec on cuda:0
print(net[1].gamma.reshape((-1,)))
print(net[1].beta.reshape((-1,)))
# 输出:
# tensor([2.3714, 2.6638, 3.9247, 0.5811, 3.4167, 2.4003], device='cuda:0', grad_fn=<ReshapeAliasBackward0>)
# tensor([ 1.6799, -1.1473, -2.5704, -1.0059, 3.6162, -0.8904], device='cuda:0', grad_fn=<ReshapeAliasBackward0>)
7.6.4 训练结果可视化
plt.savefig('OutPut.png')
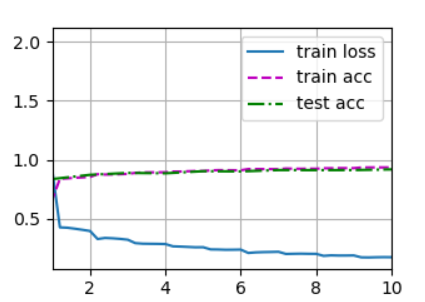
本小节完整代码如下
import torch
from torch import nn
from d2l import torch as d2l
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
torch.set_printoptions(threshold=np.inf)
# ------------------------------批量归一化层------------------------------------
# 定义批量归一化层的前向传播函数,把输入特征X进行归一化
# X:输入特征集合
# gamma:拉伸系数
# beta:偏置系数
# moving_mean:全局均值
# moving_var:全局方差
# eps:极小值
# momentum:一个批量的样本对全局样本的影响系数
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 测试模式走这里
# 如果是在预测模式下,直接利用训练时得到的全局均值和全局方差对输入特征集合进行标准化
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
# 训练模式走这里
assert len(X.shape) in (2, 4) #(如果既不是全连接层也不是卷积层,就报错)
# 如果是全连接层(全连接层第一维是批量大小,第二维是特征量)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0) # 对所有样本的每个特征各计算一次平均值
var = ((X - mean) ** 2).mean(dim=0) # 对所有样本的每个特征各计算一次方差
else:
mean = X.mean(dim=(0, 2, 3), keepdim=True) # 对属于某个通道的所有数计算平均值(包括所有样本,以及这个通道中的所有行和所有列)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True) # 对属于某个通道的所有数计算方差(包括所有样本,以及这个通道中的所有行和所有列)
# 利用均值和方差将输入特征集合X进行标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新整个训练集输入特征的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
# 利用标准化后的特征集合X以及缩放系数和偏置系数,得到标准化之后的特征集合Y,作为批量归一化层的输出
Y = gamma * X_hat + beta
return Y, moving_mean.data, moving_var.data
# 定义批量归一化层
class BatchNorm(nn.Module):
# um_features:用在全连接层后面等同于全连接层的输出个数,用在卷积层后面等同于卷积层的输出通道数
# num_dims:为2表示完全连接层,为4表示卷积层
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
# 如果用在全连接层后面
shape = (1, num_features) # (1,全连接层的输出个数)
else:
shape = (1, num_features, 1, 1) # (1,卷积层的输出通道数,1,1)
# 将拉伸系数初始化为全1
self.gamma = nn.Parameter(torch.ones(shape))
# 将偏置系数初始化为全0
self.beta = nn.Parameter(torch.zeros(shape))
# 全局均值初始化为全0
self.moving_mean = torch.zeros(shape)
# 全局方差初始化为全1
self.moving_var = torch.ones(shape)
def forward(self, X):
# 将X与moving_mean和moving_var复制到显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var
# 计算输入特征集合X的标准化结果Y,全局均值moving_mean、全局方差moving_var
Y, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean,self.moving_var, eps=1e-5, momentum=0.9)
return Y
# ------------------------------网络模型------------------------------------
net = nn.Sequential(
# 卷积核尺寸为6×6的卷积层、批量归一化层、Sigmoid激活函数层
nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
# 尺寸为2×2的平均池化层
nn.AvgPool2d(kernel_size=2, stride=2),
# 卷积核尺寸为5×5的卷积层、批量归一化层、Sigmoid激活函数层
nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
# 尺寸为2×2的平均池化层、展平层
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
# 全连接隐藏层、批量归一化层、Sigmoid激活函数层
nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
# 全连接隐藏层、批量归一化层、Sigmoid激活函数层
nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
# 全连接输出层
nn.Linear(84, 10))
# ------------------------------训练过程------------------------------------
# 定义学习率、训练轮数、批量大小
lr, num_epochs, batch_size = 1.0, 10, 256
# 下载fashion_mnist,并对数据集进行打乱和按批量大小进行切割的操作,得到可迭代的训练集和测试集(训练集和测试集的形式都为(特征数据集合,数字标签集合)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 使用GPU对模型进行训练,输出最后一轮训练时的平均损失、在训练集上的平均准确率、在测试集上的平均准测率,输出每秒能够训练多少张图像
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# 输出:
# loss 0.264, train acc 0.903, test acc 0.739
# 18366.4 examples/sec on cuda:0
print(net[1].gamma.reshape((-1,)))
print(net[1].beta.reshape((-1,)))
# 输出:
# tensor([2.3714, 2.6638, 3.9247, 0.5811, 3.4167, 2.4003], device='cuda:0', grad_fn=<ReshapeAliasBackward0>)
# tensor([ 1.6799, -1.1473, -2.5704, -1.0059, 3.6162, -0.8904], device='cuda:0', grad_fn=<ReshapeAliasBackward0>)
# ------------------------------训练结果可视化------------------------------------
plt.savefig('OutPut.png')



 浙公网安备 33010602011771号
浙公网安备 33010602011771号