4.6.0 头文件
import torch
from torch import nn
from d2l import torch as d2l
from matplotlib import pyplot as plt
4.6.1 定义dropout层
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在本情况中,所有元素都被丢弃(置0)
if dropout == 1:
return torch.zeros_like(X)
# 在本情况中,所有元素都被保留(不变)
if dropout == 0:
return X
# 生成一个随机矩阵和掩码矩阵,如果随机值大于dropout就置1,否则置0
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)
# 定义一个张量,2行8列,元素值为从0到15
X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
# 输出:
# tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
# [ 8., 9., 10., 11., 12., 13., 14., 15.]])
# print(dropout_layer(X, 0.))
# 输出:
# tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
# [ 8., 9., 10., 11., 12., 13., 14., 15.]])
print(dropout_layer(X, 0.5))
# 输出:
# tensor([[ 0., 2., 4., 0., 8., 10., 0., 0.],
# [ 0., 18., 20., 22., 24., 0., 28., 0.]])
print(dropout_layer(X, 1.))
# 输出:
# tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
# [0., 0., 0., 0., 0., 0., 0., 0.]])
4.6.2 定义网络模型
# 输入特征维度、输出特征维度、隐藏层1维度、隐藏层2维度
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
# dropout1层的概率,dropout2层的概率
dropout1, dropout2 = 0.2, 0.5
# 定义网络模型
class Net(nn.Module):
# 定义构造函数
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,is_training = True):
# 调用父类的构造函数
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training #是训练还是测试
# 定义全连接层1,全连接层输入维度num_inputs(784(28×28)),隐藏层1维度num_hiddens1(256)
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
# 定义全连接层2,隐藏层1维度num_hiddens1(256),隐藏层2维度num_hiddens1(256)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
# 定义全连接层3,隐藏层2维度num_hiddens1(256),输出特征维度num_outputs(10)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
# relu激活函数
self.relu = nn.ReLU()
def forward(self, X):
# 如果是训练模型:
# 全连接层1 → relu层 → dropout层 → 全连接层2 → relu层 → dropout层 → 全连接层3
# 如果是测试模型:
# 全连接层1 → relu层 → 全连接层2 → relu层 → 全连接层3
H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
# 只有在训练模型时才使用dropout
if self.training == True:
# 在第一个全连接层之后添加一个dropout层
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training == True:
# 在第二个全连接层之后添加一个dropout层
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return out
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
4.6.3 定义损失函数
# 定义交叉熵损失函数
loss = nn.CrossEntropyLoss(reduction='none')
4.6.4 下载fashion_mnist数据集
# 定义批量大小
batch_size = 256
# 下载fashion_mnist,并对数据集进行打乱和按批量大小进行切割的操作,得到可迭代的训练集和测试集(训练集和测试集的形式都为(特征数据集合,数字标签集合))
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
4.6.5 定义优化器
# 定义学习率
lr = 0.5
# 定义随机梯度下降优化器
trainer = torch.optim.SGD(net.parameters(), lr=lr)
4.6.6 训练过程
# 定义训练轮数、学习率
num_epochs = 10
# 开始训练
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
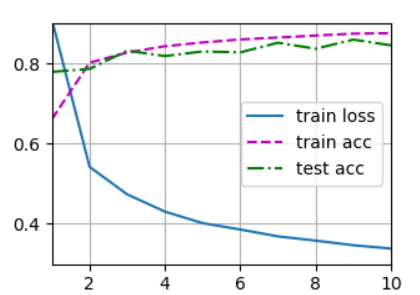
4.6.7 训练结果可视化
plt.savefig('OutPut.png')
本小节完整代码如下
import torch
from torch import nn
from d2l import torch as d2l
from matplotlib import pyplot as plt
# ------------------------------定义dropout层------------------------------------
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在本情况中,所有元素都被丢弃(置0)
if dropout == 1:
return torch.zeros_like(X)
# 在本情况中,所有元素都被保留(不变)
if dropout == 0:
return X
# 生成一个随机矩阵和掩码矩阵,如果随机值大于dropout就置1,否则置0
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)
# 定义一个张量,2行8列,元素值为从0到15
X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
# 输出:
# tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
# [ 8., 9., 10., 11., 12., 13., 14., 15.]])
# print(dropout_layer(X, 0.))
# 输出:
# tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
# [ 8., 9., 10., 11., 12., 13., 14., 15.]])
print(dropout_layer(X, 0.5))
# 输出:
# tensor([[ 0., 2., 4., 0., 8., 10., 0., 0.],
# [ 0., 18., 20., 22., 24., 0., 28., 0.]])
print(dropout_layer(X, 1.))
# 输出:
# tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
# [0., 0., 0., 0., 0., 0., 0., 0.]])
# ------------------------------定义网络模型------------------------------------
# 输入特征维度、输出特征维度、隐藏层1维度、隐藏层2维度
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
# dropout1层的概率,dropout2层的概率
dropout1, dropout2 = 0.2, 0.5
# 定义网络模型
class Net(nn.Module):
# 定义构造函数
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,is_training = True):
# 调用父类的构造函数
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training #是训练还是测试
# 定义全连接层1,全连接层输入维度num_inputs(784(28×28)),隐藏层1维度num_hiddens1(256)
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
# 定义全连接层2,隐藏层1维度num_hiddens1(256),隐藏层2维度num_hiddens1(256)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
# 定义全连接层3,隐藏层2维度num_hiddens1(256),输出特征维度num_outputs(10)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
# relu激活函数
self.relu = nn.ReLU()
def forward(self, X):
# 如果是训练模型:
# 全连接层1 → relu层 → dropout层 → 全连接层2 → relu层 → dropout层 → 全连接层3
# 如果是测试模型:
# 全连接层1 → relu层 → 全连接层2 → relu层 → 全连接层3
H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
# 只有在训练模型时才使用dropout
if self.training == True:
# 在第一个全连接层之后添加一个dropout层
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training == True:
# 在第二个全连接层之后添加一个dropout层
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return out
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
# ------------------------------定义损失函数------------------------------------
# 定义交叉熵损失函数
loss = nn.CrossEntropyLoss(reduction='none')
# ------------------------------下载fashion_mnist数据集------------------------------------
# 定义批量大小
batch_size = 256
# 下载fashion_mnist,并对数据集进行打乱和按批量大小进行切割的操作,得到可迭代的训练集和测试集(训练集和测试集的形式都为(特征数据集合,数字标签集合))
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# ------------------------------定义优化器------------------------------------
# 定义学习率
lr = 0.5
# 定义随机梯度下降优化器
trainer = torch.optim.SGD(net.parameters(), lr=lr)
# ------------------------------训练过程------------------------------------
# 定义训练轮数、学习率
num_epochs = 10
# 开始训练
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
# ------------------------------训练结果可视化------------------------------------
plt.savefig('OutPut.png')


 浙公网安备 33010602011771号
浙公网安备 33010602011771号