4.5 L2正则化从零实现

 

4.5.0 头文件

import torch
from torch import nn
from d2l import torch as d2l
from matplotlib import pyplot as plt

 

4.5.1 初始化模型权重和偏移量

# 训练集样本数、测试集样本数、样本维度、批量大小
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5

# 设置真实权重w，元素值全为0.01，设置真实偏移量b为0.05
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05

# 用数据集生成器训练集
train_data = d2l.synthetic_data(true_w, true_b, n_train)
# 将训练集打乱，然后按照批量大小进行切割和封装
train_iter = d2l.load_array(train_data, batch_size)
# 用数据集生成器生成测试集
test_data = d2l.synthetic_data(true_w, true_b, n_test)
# 将测试集按照批量大小进行切割和封装
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

 

4.5.2 初始化模型权重和偏移量

# 初始化模型权重和偏移量
def init_params():
    # 将权重元素按照标准正态分布进行初始化
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    # 将偏移量初始化为0
    b = torch.zeros(1, requires_grad=True)
    # 返回权重和偏移量
    return [w, b]

# L2惩罚项
def l2_penalty(w):
    # 返回L2正则项(每隔权重的平方和除以2)
    return torch.sum(w.pow(2)) / 2

 

4.5.3 训练过程

 

def train(lambd):
    # 初始化模型权重和偏移量
    w, b = init_params()

    # 定义一个匿名函数,函数名为net,函数形参为X,函数体为d2l.linreg(X, w, b),作用就是定义一个网络模型
    net = lambda X: d2l.linreg(X, w, b)

    # 定义均方损失函数
    loss = d2l.squared_loss

    # 设置训练轮数、学习率
    num_epochs, lr = 100, 0.003

    # 定义一个动画来将训练结果可视化
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])

    # 对于每一轮训练
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 对于每一个批量的数据
            # 计算该批量的预测损失时,增加L2正则项惩罚，lambd为系数
            l = loss(net(X), y) + lambd * l2_penalty(w)
            # 使用随机梯度下降算法来优化权重和偏移量
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        # 每隔5轮训练,将训练得到的模型在训练集和测试集上分别计算一次损失（训练损失、泛化损失）
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))
    # 计算权重w的L2范数,即矩阵中各元素的平方和再开根号
    print('w的L2范数是：', torch.norm(w).item())

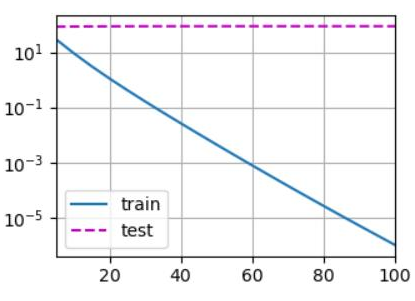
# 不使用L2正则项(不使用权重衰减)
train(lambd=0)
# 输出:
# w的L2范数是： 13.332711219787598

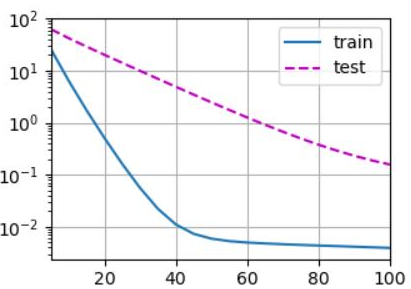
# 使用L2正则项(使用权重衰减)
train(lambd=3)
# 输出:
# w的L2范数是： 0.39131948351860046

 

 

 

 

 

4.5.4 可视化训练结果

plt.savefig('Output.png')

 

本小节完整代码如下

 

# ------------------------------制作数据集------------------------------------

# 训练集样本数、测试集样本数、样本维度、批量大小
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5

# 设置真实权重w，元素值全为0.01，设置真实偏移量b为0.05
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05

# 用数据集生成器训练集
train_data = d2l.synthetic_data(true_w, true_b, n_train)
# 将训练集打乱，然后按照批量大小进行切割和封装
train_iter = d2l.load_array(train_data, batch_size)
# 用数据集生成器生成测试集
test_data = d2l.synthetic_data(true_w, true_b, n_test)
# 将测试集按照批量大小进行切割和封装
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

# ------------------------------初始化模型权重和偏移量------------------------------------

# 初始化模型权重和偏移量
def init_params():
    # 将权重元素按照标准正态分布进行初始化
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    # 将偏移量初始化为0
    b = torch.zeros(1, requires_grad=True)
    # 返回权重和偏移量
    return [w, b]

# L2惩罚项
def l2_penalty(w):
    # 返回L2正则项(每隔权重的平方和除以2)
    return torch.sum(w.pow(2)) / 2

# ------------------------------训练过程------------------------------------

def train(lambd):
    # 初始化模型权重和偏移量
    w, b = init_params()

    # 定义一个匿名函数,函数名为net,函数形参为X,函数体为d2l.linreg(X, w, b),作用就是定义一个网络模型
    net = lambda X: d2l.linreg(X, w, b)

    # 定义均方损失函数
    loss = d2l.squared_loss

    # 设置训练轮数、学习率
    num_epochs, lr = 100, 0.003

    # 定义一个动画来将训练结果可视化
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])

    # 对于每一轮训练
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 对于每一个批量的数据
            # 计算该批量的预测损失时,增加L2正则项惩罚，lambd为系数
            l = loss(net(X), y) + lambd * l2_penalty(w)
            # 使用随机梯度下降算法来优化权重和偏移量
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        # 每隔5轮训练,将训练得到的模型在训练集和测试集上分别计算一次损失（训练损失、泛化损失）
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))
    # 计算权重w的L2范数,即矩阵中各元素的平方和再开根号
    print('w的L2范数是：', torch.norm(w).item())

# 不使用L2正则项(不使用权重衰减)
train(lambd=0)
# 输出:
# w的L2范数是： 13.332711219787598

# 使用L2正则项(使用权重衰减)
train(lambd=3)
# 输出:
# w的L2范数是： 0.39131948351860046

# ------------------------------可视化训练结果------------------------------------

plt.savefig('Output.png')