手把手带你从零推导旋转位置编码RoPE

RNN每个step的隐状态都取决于上一个step的输出，这种连续的状态转移方式使得RNN天然带有位置信息。而Transformer仅依靠Attention机制来关注序列中不同token之间的相关性，如果只使用token embedding就无法获得句子中字与字之间的位置信息，也就是说如果没有位置编码，输入“我不爱你”与“不我爱你”的效果是相同的，因此我们要在里面额外引入位置信息。下面我就为大家介绍位置编码的发展过程。

1.绝对位置编码

1.1函数式绝对位置编码 

 python代码实现：

import numpy as np
import matplotlib.pyplot as plt

def absolute_positional_encoding(max_len, d_model):
    """
    生成绝对位置编码矩阵
    
    参数:
        max_len: 序列最大长度
        d_model: 嵌入维度
        
    返回:
        pe: 位置编码矩阵，形状为(max_len, d_model)
    """
    position = np.arange(max_len)[:, np.newaxis]
    div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
    
    pe = np.zeros((max_len, d_model))
    pe[:, 0::2] = np.sin(position * div_term)
    pe[:, 1::2] = np.cos(position * div_term)
    
    return pe

# 示例使用
max_len = 100
d_model = 64
pe = absolute_positional_encoding(max_len, d_model)

# 可视化位置编码
plt.figure(figsize=(10, 6))
plt.imshow(pe.T, cmap='viridis', aspect='auto')
plt.xlabel('Position')
plt.ylabel('Dimension')
plt.colorbar()
plt.title('Absolute Positional Encoding')
plt.show()

　　pytorch实现：

import torch
import torch.nn as nn

class LearnedPositionalEncoding(nn.Module):
    """
    可学习的绝对位置编码
    
    参数:
        d_model: 嵌入维度
        max_len: 最大序列长度
    """
    def __init__(self, d_model, max_len=512):
        super(LearnedPositionalEncoding, self).__init__()
        self.position_embeddings = nn.Parameter(torch.zeros(max_len, d_model))
        self.reset_parameters()
    
    def reset_parameters(self):
        nn.init.normal_(self.position_embeddings, mean=0.0, std=0.02)
    
    def forward(self, x):
        """
        参数:
            x: 输入张量，形状为 (batch_size, seq_len, d_model)
        返回:
            添加了位置编码的张量
        """
        positions = torch.arange(x.size(1), device=x.device).unsqueeze(0)  # (1, seq_len)
        pos_emb = self.position_embeddings[positions]  # (1, seq_len, d_model)
        return x + pos_emb

# 使用示例
batch_size, seq_len, d_model = 4, 10, 512
x = torch.randn(batch_size, seq_len, d_model)
pos_enc = LearnedPositionalEncoding(d_model, max_len=20)
output = pos_enc(x)
print(output.shape)  # torch.Size([4, 10, 512])

　　

1.2训练式绝对位置编码

基于万物皆可训练的思想诞生了训练式绝对位置编码，它根据位置信息编码id，再通过Embedding层，学习该位置Embedding参数，比如Bert最大长度为512，编码维度为768，那么就初始化一个512×768的矩阵作为位置向量，让它随着训练过程更新。

从BERT提出后，大部分模型的位置编码都遵循这种方式，但这种位置编码有一个缺陷，就是它不具备外推性能，是指一旦我们在预测时的序列长度超过了训练阶段的长度，它的位置信息就位于模型的盲区，需要重新训练更长的位置编码。

 

import torch
import torch.nn as nn

class LearnedPositionalEncoding(nn.Module):
    """
    可学习的绝对位置编码
    
    参数:
        d_model: 嵌入维度
        max_len: 最大序列长度
    """
    def __init__(self, d_model, max_len=512):
        super(LearnedPositionalEncoding, self).__init__()
        self.position_embeddings = nn.Parameter(torch.zeros(max_len, d_model))
        self.reset_parameters()
    
    def reset_parameters(self):
        nn.init.normal_(self.position_embeddings, mean=0.0, std=0.02)
    
    def forward(self, x):
        """
        参数:
            x: 输入张量，形状为 (batch_size, seq_len, d_model)
        返回:
            添加了位置编码的张量
        """
        positions = torch.arange(x.size(1), device=x.device).unsqueeze(0)  # (1, seq_len)
        pos_emb = self.position_embeddings[positions]  # (1, seq_len, d_model)
        return x + pos_emb

# 使用示例
batch_size, seq_len, d_model = 4, 10, 512
x = torch.randn(batch_size, seq_len, d_model)
pos_enc = LearnedPositionalEncoding(d_model, max_len=20)
output = pos_enc(x)
print(output.shape)  # torch.Size([4, 10, 512])

2.相对位置编码

绝对和相对在概念上理解是很简单的，但它们在Transformer的实现上是完全不一样的。

l 由于绝对位置编码只关注单个位置信息，因此它的实现通常在输入层，可以通过简单的向量相加融入模型

l 而相对位置一定是pair对（某两个token之间）的信息，因此它无法直接在输入层实现，通常是通过改变Attention_score的计算方式来实现

 

 

 

 

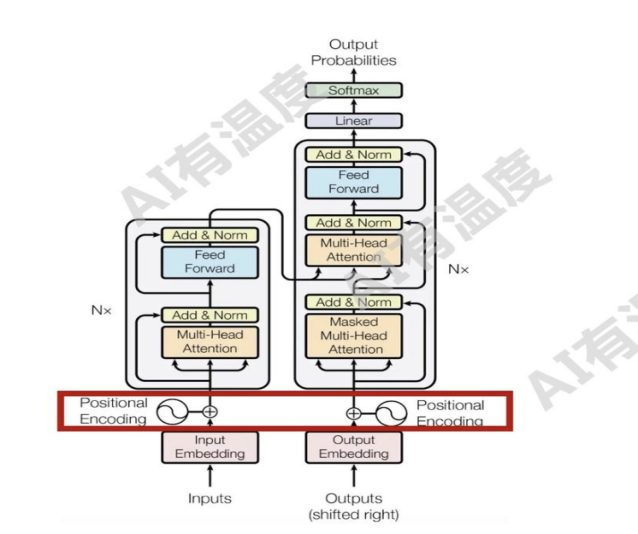
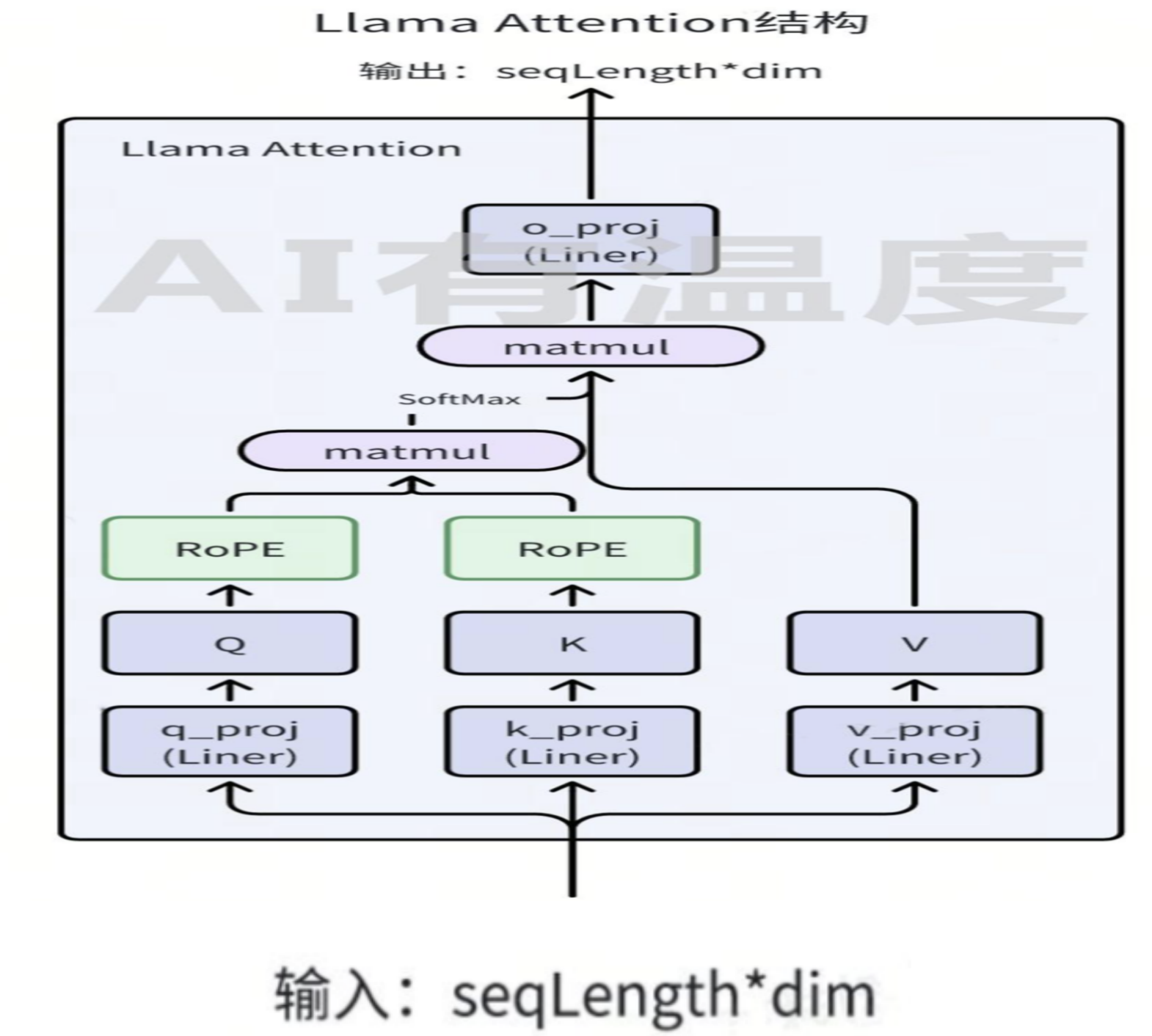
比如在LLaMA模型结构中，计算相对位置编码就是在计算Attention_score的同时实现的。而相对位置编码在计算方法上也可以分为训练式相对位置编码与函数式相对位置编码。

2.1训练式相对位置编码

 代码实现：

import torch
import torch.nn as nn
import math

class RelativePositionalBias(nn.Module):
    """
    可学习的相对位置偏置（Transformer-XL风格）
    
    参数:
        max_positions: 最大相对位置距离（正负方向）
        num_heads: 注意力头数
    """
    def __init__(self, max_positions=128, num_heads=8):
        super().__init__()
        self.max_positions = max_positions
        self.num_heads = num_heads
        self.rel_pos_bias = nn.Embedding(2 * max_positions + 1, num_heads)
        
        # 初始化
        nn.init.normal_(self.rel_pos_bias.weight, mean=0.0, std=0.02)
    
    def forward(self, q_len, k_len):
        """
        参数:
            q_len: query序列长度
            k_len: key序列长度
        返回:
            相对位置偏置矩阵，形状为 (num_heads, q_len, k_len)
        """
        # 生成相对位置索引
        context_position = torch.arange(q_len, dtype=torch.long)[:, None]
        memory_position = torch.arange(k_len, dtype=torch.long)[None, :]
        relative_position = memory_position - context_position  # shape (q_len, k_len)
        
        # 裁剪到最大位置范围
        relative_position = relative_position.clamp(-self.max_positions, self.max_positions)
        relative_position += self.max_positions  # 转换为非负索引
        
        # 获取偏置并调整形状
        bias = self.rel_pos_bias(relative_position)  # (q_len, k_len, num_heads)
        bias = bias.permute(2, 0, 1)  # (num_heads, q_len, k_len)
        
        return bias

# 使用示例
max_positions, num_heads = 64, 8
q_len, k_len = 10, 15
rel_pos_bias = RelativePositionalBias(max_positions, num_heads)
bias = rel_pos_bias(q_len, k_len)
print(bias.shape)  # torch.Size([8, 10, 15])

　　

2.2 函数式相对位置编码

 

 

 

 

 

 

 

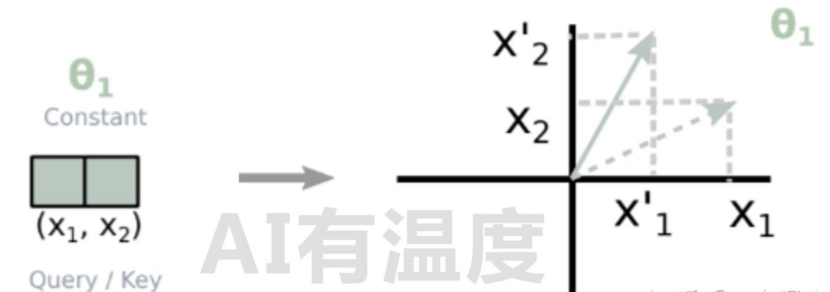
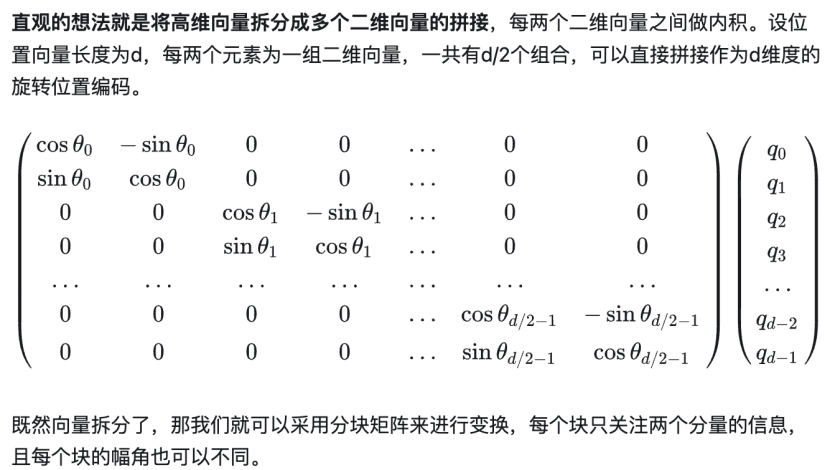
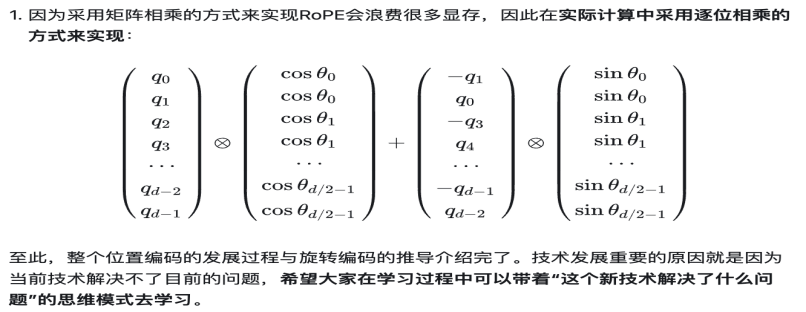
代码实现：

import torch
import torch.nn as nn
import math

class FunctionalRelativePositionalEncoding(nn.Module):
    """
    函数式相对位置编码实现
    
    参数:
        max_len: 最大序列长度
        d_model: 模型维度
        dropout_rate: dropout概率
    """
    def __init__(self, max_len=512, d_model=512, dropout_rate=0.1):
        super().__init__()
        self.d_model = d_model
        self.dropout = nn.Dropout(dropout_rate)
        
        # 创建相对位置矩阵
        position = torch.arange(max_len).unsqueeze(1)
        rel_pos = position - torch.arange(max_len).unsqueeze(0)
        rel_pos = rel_pos.clamp(-max_len + 1, max_len - 1)
        
        # 预计算正弦/余弦编码
        pe = self._positional_encoding(rel_pos, d_model)
        self.register_buffer('pe', pe)
        
        # 可学习的相对位置偏置 (可选)
        self.rel_pos_bias = nn.Parameter(torch.zeros(2 * max_len - 1, d_model))
        nn.init.xavier_uniform_(self.rel_pos_bias)
    
    def _positional_encoding(self, rel_pos, d_model):
        """生成相对位置编码"""
        # 将相对位置映射到[0, 2*max_len-2]范围
        rel_pos = rel_pos + (2 * self.pe.size(0) // 2 - 1)
        
        # 初始化位置编码矩阵
        pe = torch.zeros(rel_pos.size(0), rel_pos.size(1), d_model)
        
        # 计算每个维度的位置编码
        position = rel_pos.float().unsqueeze(-1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * 
                           (-math.log(10000.0) / d_model))
        
        pe[..., 0::2] = torch.sin(position * div_term)
        pe[..., 1::2] = torch.cos(position * div_term)
        
        return pe
    
    def forward(self, x):
        """
        x: 输入张量，形状为 (batch_size, seq_len, d_model)
        返回: 添加了相对位置编码的张量
        """
        batch_size, seq_len, _ = x.size()
        
        # 获取当前序列长度的相对位置编码
        rel_pe = self.pe[:seq_len, :seq_len]
        
        # 可选：添加可学习的相对位置偏置
        rel_bias = self.rel_pos_bias[(2 * seq_len - 1) // 2 - (seq_len - 1) : 
                                    (2 * seq_len - 1) // 2 + seq_len]
        rel_pe = rel_pe + rel_bias.unsqueeze(1)
        
        # 将相对位置编码应用到注意力分数上
        # 在实际Transformer实现中，这通常是在注意力计算时完成的
        # 这里我们简单地将编码添加到输入中作为示例
        x = x + rel_pe.mean(dim=0)  # 简化处理
        
        return self.dropout(x)