异常检测：K-Means算法

K-Means算法是一个聚类算法，在样本没有类别的情况下可以通过算法聚出类别，比如某公司中有大量的用户，现在需要我们将用户划分出类别，但是现在我们并不知道怎么划分更好，这个时候就可以通过K-Means算法来帮助我们划分出类别。其原理是通过计算样本到质心的距离来对样本聚出类别，其中的距离我们可以理解为样本间的相似性，也就是“物以类聚”。

其中提到的质心是通过所有样本点的均值来计算出来的，如果存在异常值那么就会导致质心的计算出现偏差。进而影响结果。如图2-1：在没有异常值的情况下的质心的计算和聚类结果：

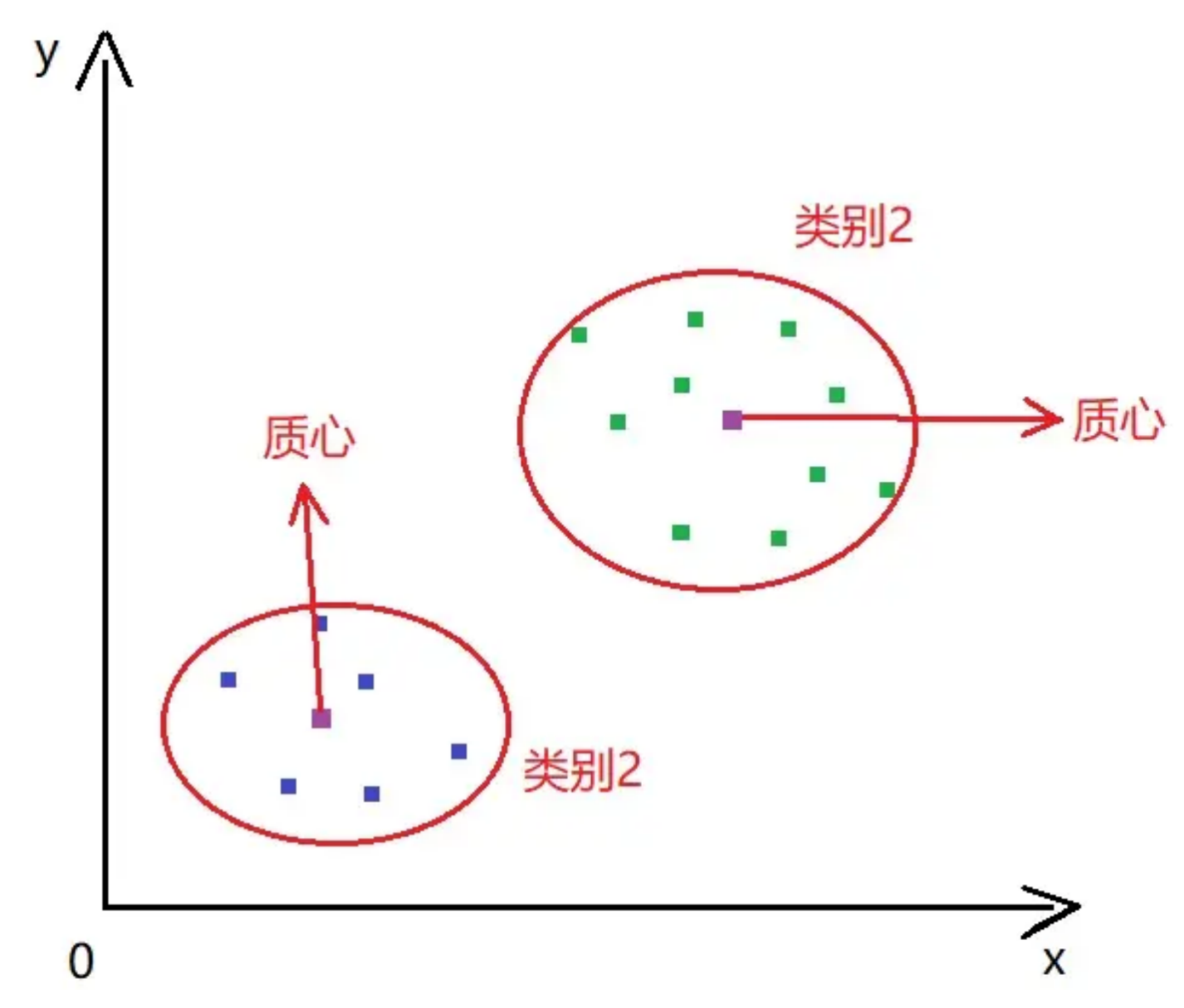
图2-1

通过图2-1我们可以看出聚类的结果还是比较理想的，接下来我们引入一个异常值，再看下聚类结果的变化，如图2-2：

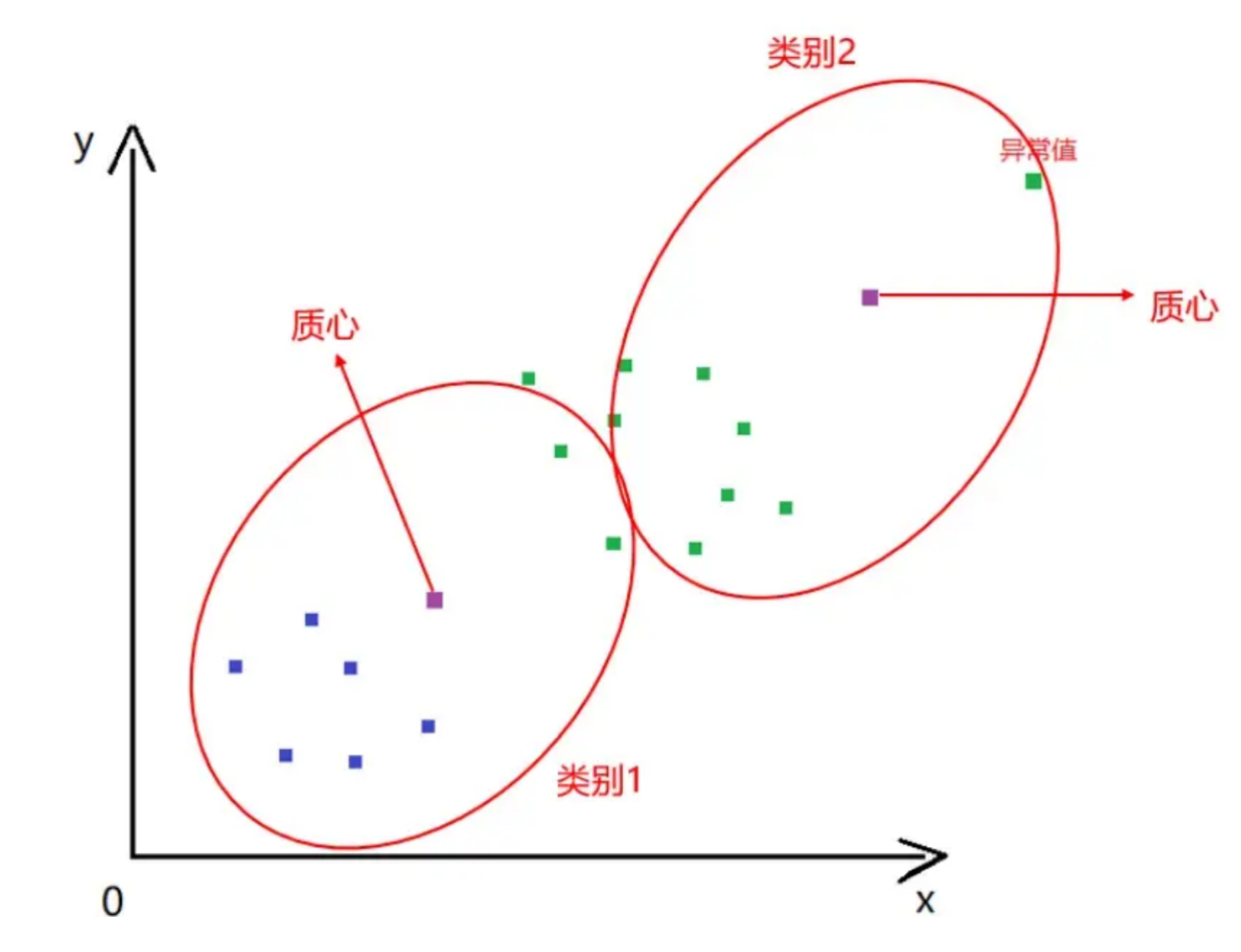
图2-2

通过图2-2可以看出，异常值导致聚类的结果出现了错误，让本应该是类别2的样本分到了类别1中。

因此在机器学习中异常值的存在对算法最终的结果影响还是很大的，那么就需要我们在机器学习中对异常值进行处理。

一、K-Means算法原理

K-Means算法：

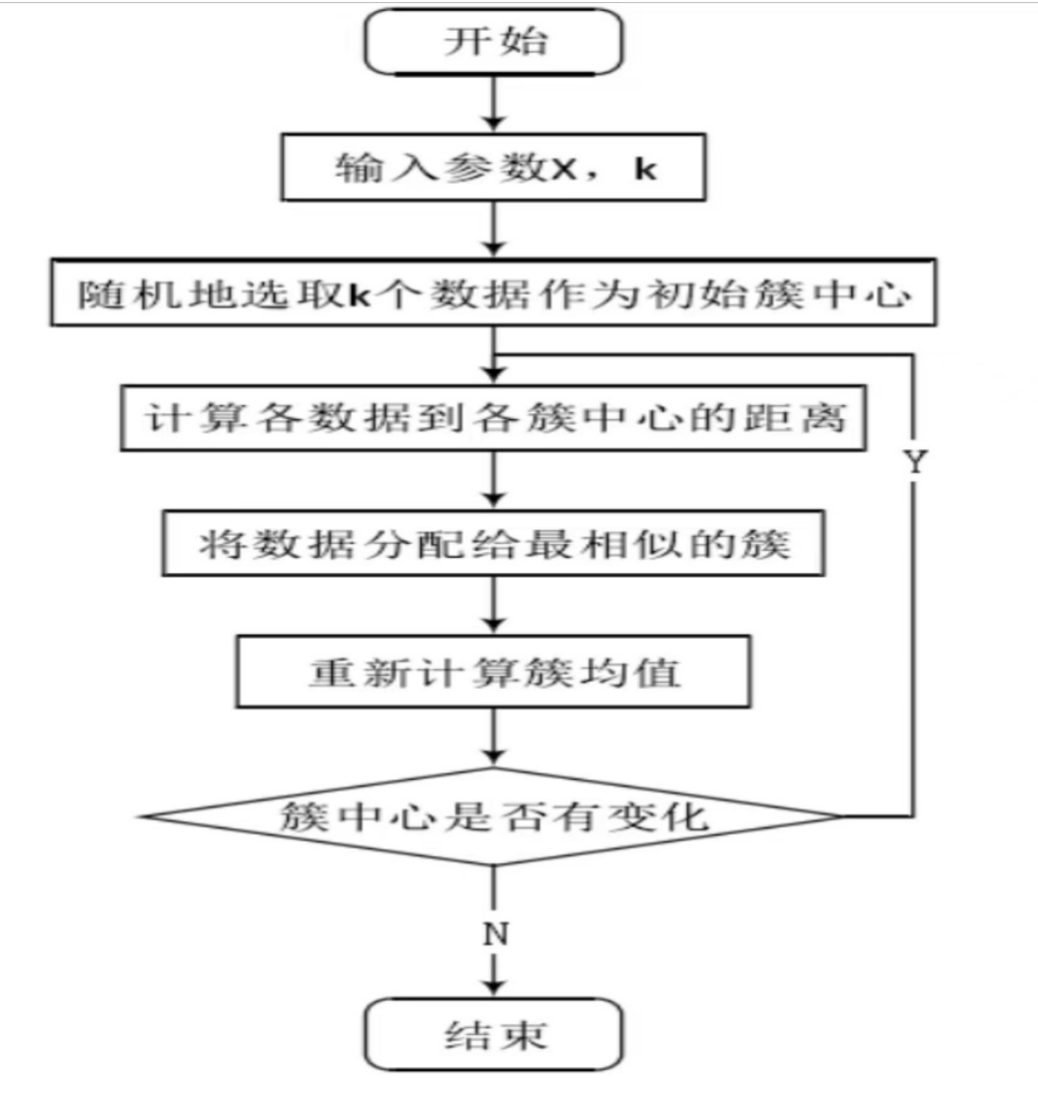
图2-3

如图2-3所示：

1. 对于给定的一组数据，随机初始化K个聚类中心（簇中心）

2. 计算每个数据到簇中心的距离（一般采用欧氏距离），并把该数据归为离它最近的簇。

3. 根据得到的簇，重新计算簇中心。

4. 对步骤2、步骤3进行迭代直至簇中心不再改变或者小于指定阈值。

二、K-means实现（Python3）

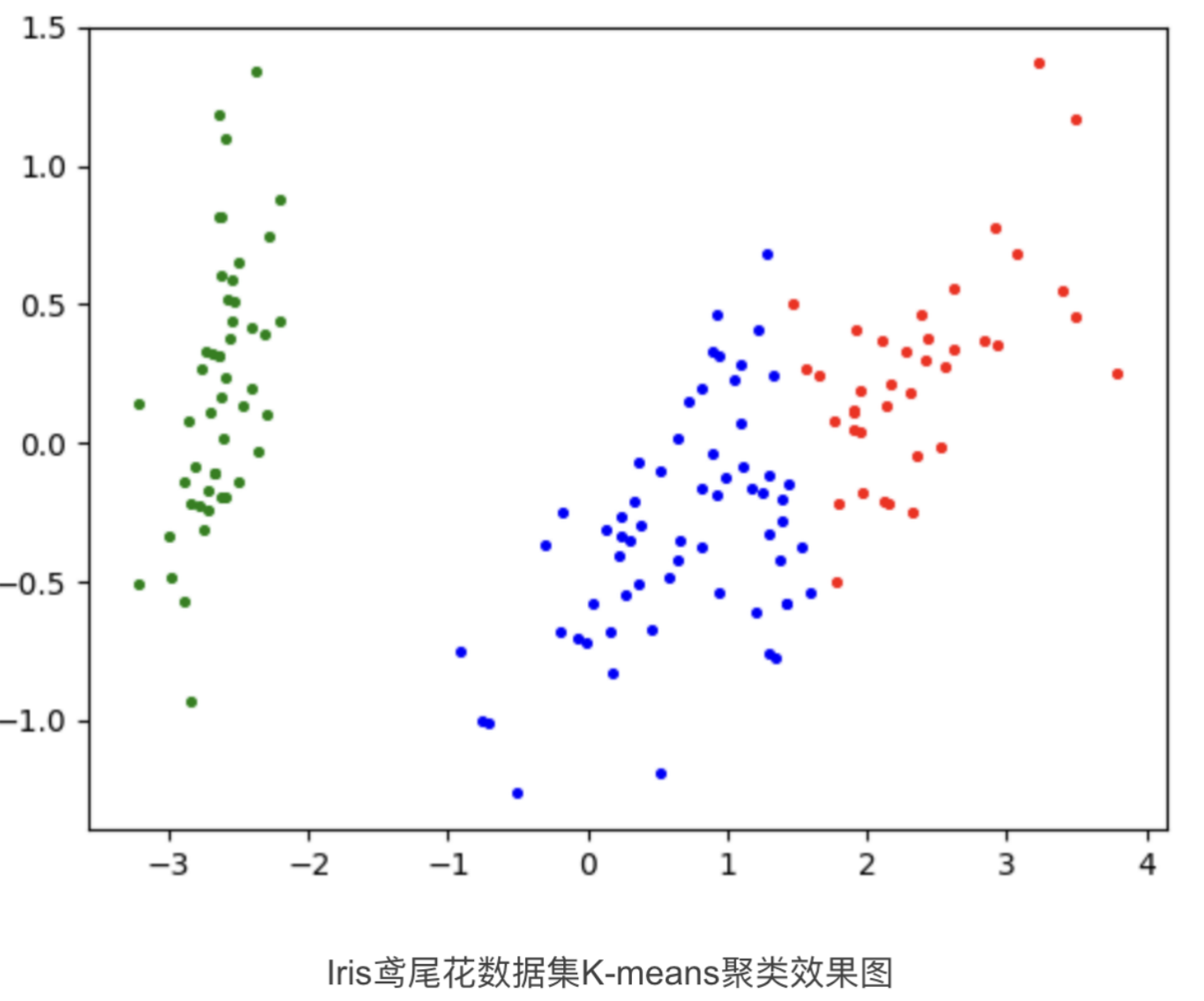
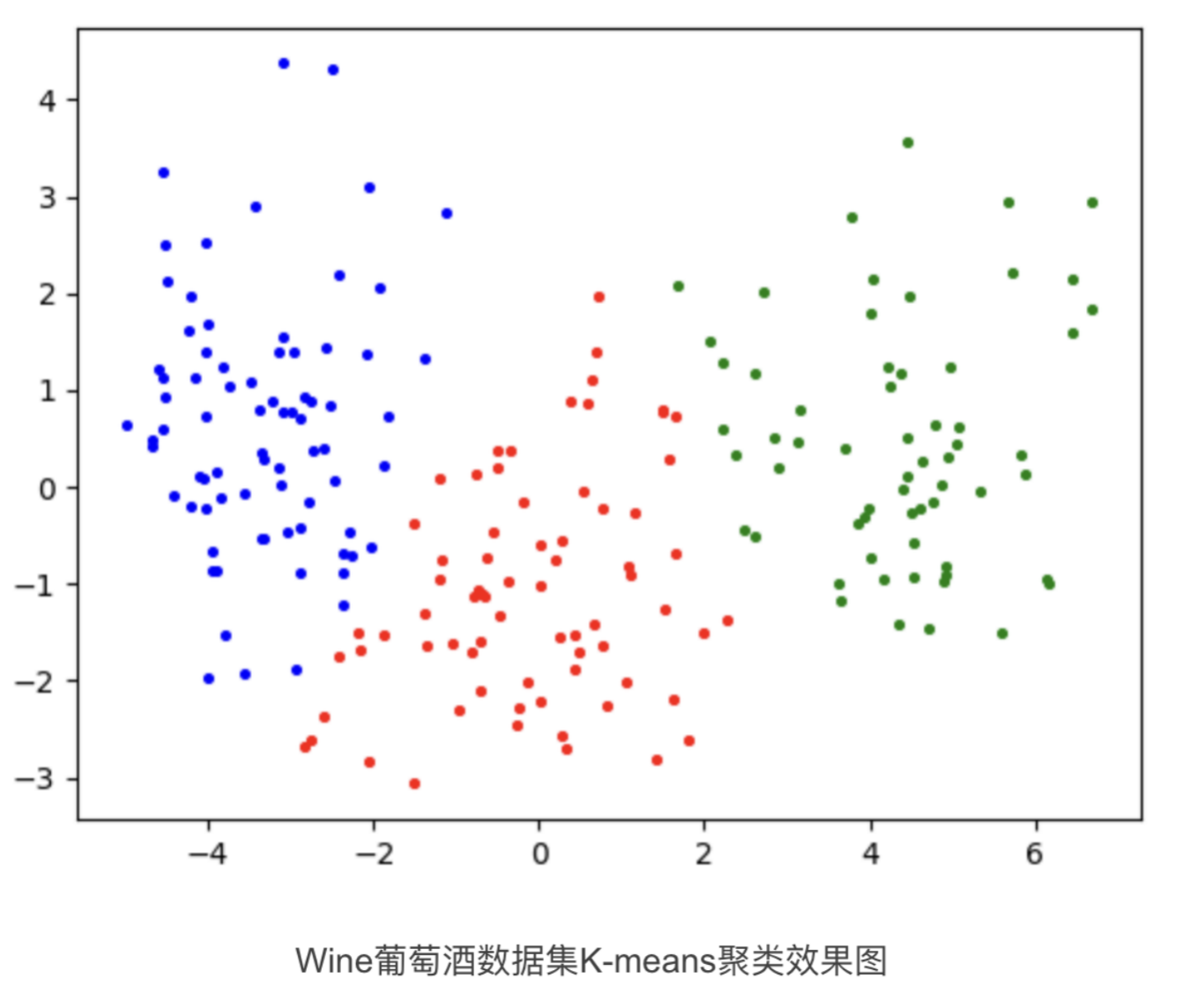
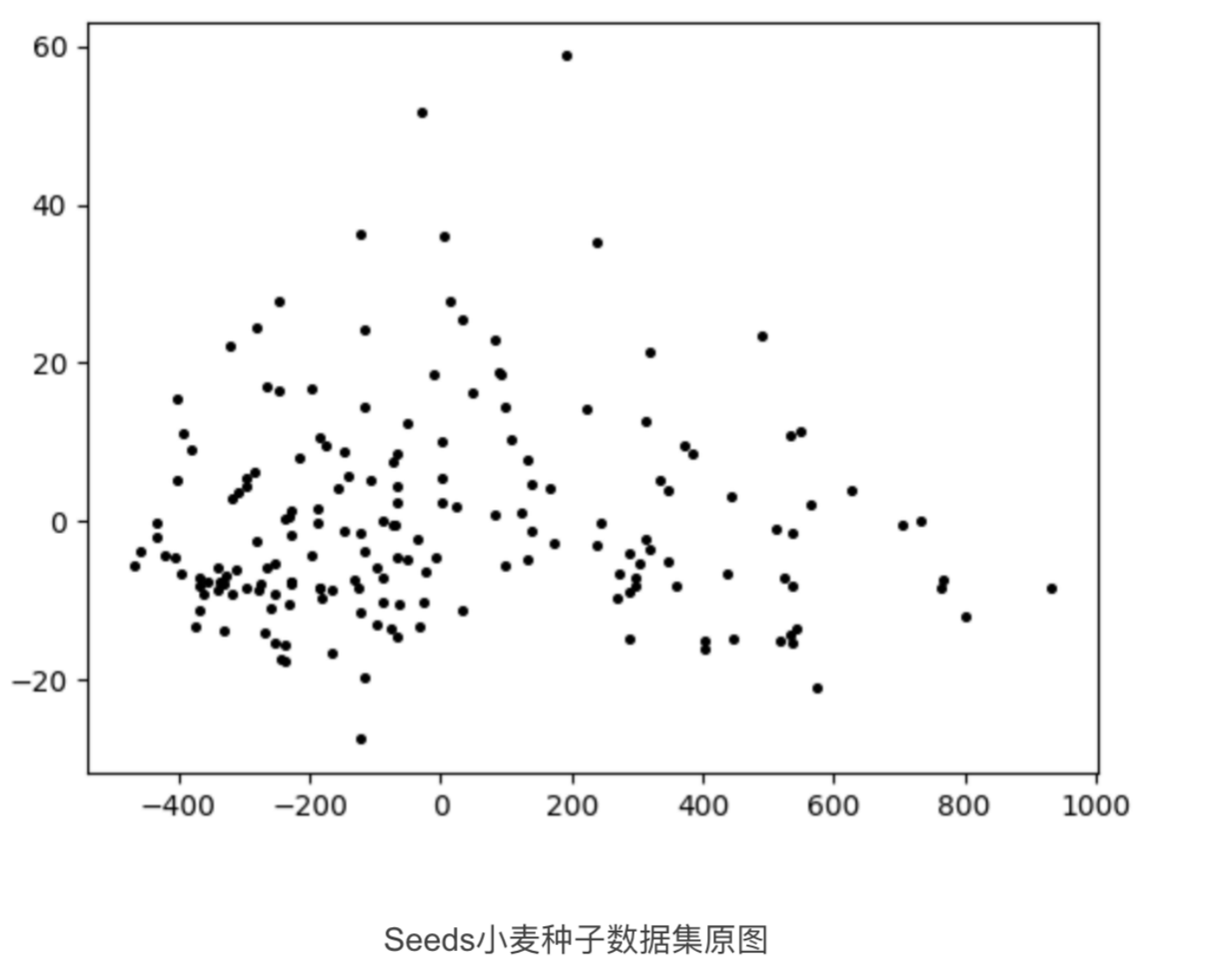
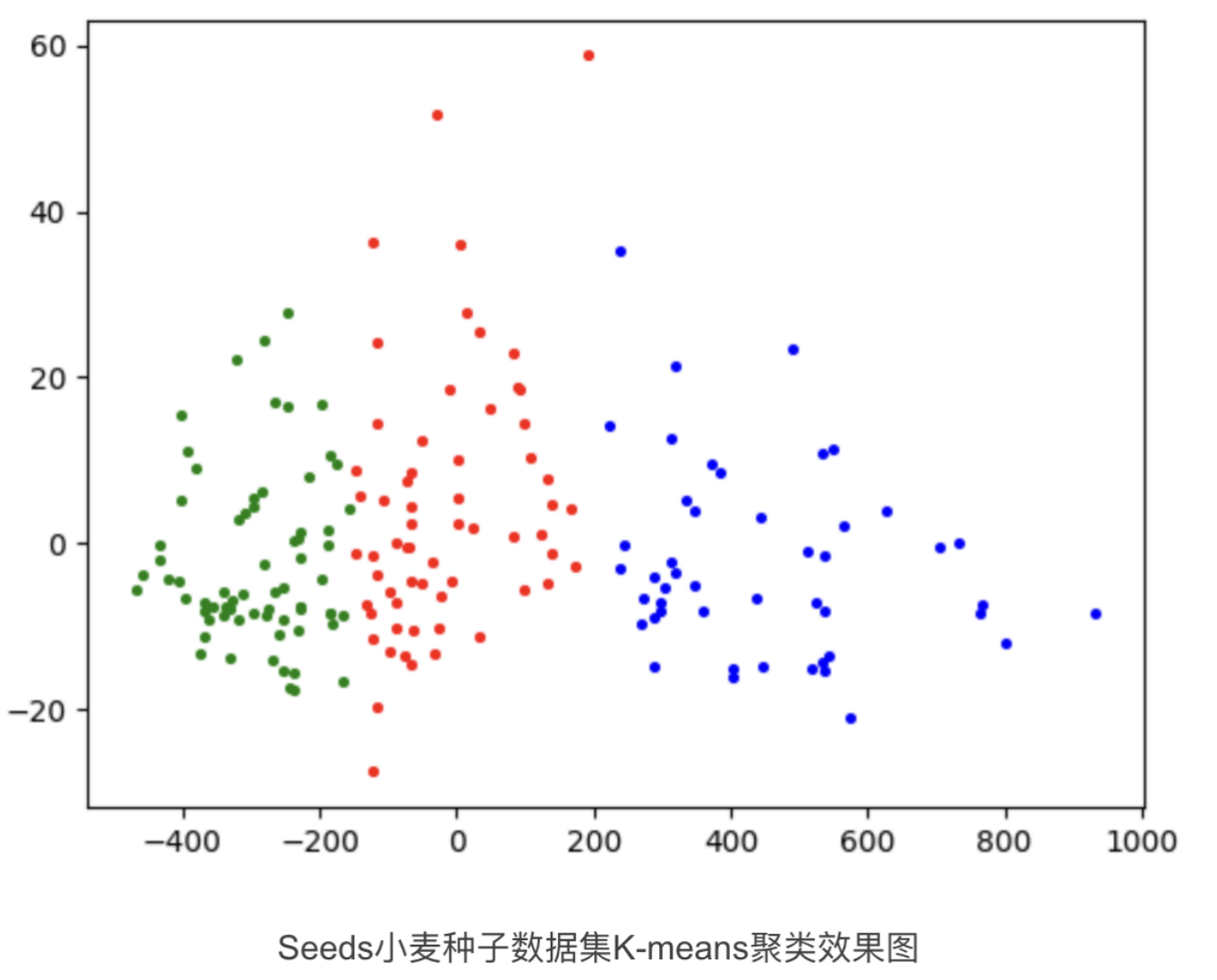
本文使用的数据集为UCI数据集，分别使用鸢尾花数据集Iris、葡萄酒数据集Wine、小麦种子数据集seeds进行测试，本文从UCI官网上将这三个数据集下载下来，并放入和python文件同一个文件夹内即可。同时由于程序需要，将数据集的列的位置做出了略微改动。数据集具体信息如下表：

代码如下：

import time
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from numpy import nonzero, array
from sklearn.cluster import KMeans
from sklearn.metrics import f1_score, accuracy_score, normalized_mutual_info_score, rand_score, adjusted_rand_score
from sklearn.preprocessing import LabelEncoder
from sklearn.decomposition import PCA

# 数据保存在.csv文件中
iris = pd.read_csv("dataset/Iris.csv", header=0)  # 鸢尾花数据集 Iris  class=3
wine = pd.read_csv("dataset/wine.csv")  # 葡萄酒数据集 Wine  class=3
seeds = pd.read_csv("dataset/seeds.csv")  # 小麦种子数据集 seeds  class=3
wdbc = pd.read_csv("dataset/wdbc.csv")  # 威斯康星州乳腺癌数据集 Breast Cancer Wisconsin (Diagnostic)  class=2
glass = pd.read_csv("dataset/glass.csv")  # 玻璃辨识数据集 Glass Identification  class=6
df = iris  # 设置要读取的数据集

columns = list(df.columns)  # 获取数据集的第一行，第一行通常为特征名，所以先取出
features = columns[:len(columns) - 1]  # 数据集的特征名（去除了最后一列，因为最后一列存放的是标签，不是数据）
dataset = df[features]  # 预处理之后的数据，去除掉了第一行的数据（因为其为特征名，如果数据第一行不是特征名，可跳过这一步）
attributes = len(df.columns) - 1  # 属性数量（数据集维度）
original_labels = list(df[columns[-1]])  # 原始标签

def initialize_centroids(data, k):
    # 从数据集中随机选择k个点作为初始质心
    centers = data[np.random.choice(data.shape[0], k, replace=False)]
    return centers

def get_clusters(data, centroids):
    # 计算数据点与质心之间的距离，并将数据点分配给最近的质心
    distances = np.linalg.norm(data[:, np.newaxis] - centroids, axis=2)
    cluster_labels = np.argmin(distances, axis=1)
    return cluster_labels


def update_centroids(data, cluster_labels, k):
    # 计算每个簇的新质心，即簇内数据点的均值
    new_centroids = np.array([data[cluster_labels == i].mean(axis=0) for i in range(k)])
    return new_centroids

def k_means(data, k, T, epsilon):
    start = time.time()  # 开始时间，计时
    # 初始化质心
    centroids = initialize_centroids(data, k)
    t = 0
    while t <= T:
        # 分配簇
        cluster_labels = get_clusters(data, centroids)
        # 更新质心
        new_centroids = update_centroids(data, cluster_labels, k)

        # 检查收敛条件
        if np.linalg.norm(new_centroids - centroids) < epsilon:
            break
        centroids = new_centroids
        print("第", t, "次迭代")
        t += 1
    print("用时：{0}".format(time.time() - start))
    return cluster_labels, centroids


# 计算聚类指标
def clustering_indicators(labels_true, labels_pred):
    if type(labels_true[0]) != int:
        labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]])  # 如果数据集的标签为文本类型，把文本标签转换为数字标签
    f_measure = f1_score(labels_true, labels_pred, average='macro')  # F值
    accuracy = accuracy_score(labels_true, labels_pred)  # ACC
    normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred)  # NMI
    rand_index = rand_score(labels_true, labels_pred)  # RI
    ARI = adjusted_rand_score(labels_true, labels_pred)
    return f_measure, accuracy, normalized_mutual_information, rand_index, ARI

# 绘制聚类结果散点图
def draw_cluster(dataset, centers, labels):
    center_array = array(centers)
    if attributes > 2:
        dataset = PCA(n_components=2).fit_transform(dataset)  # 如果属性数量大于2，降维
        center_array = PCA(n_components=2).fit_transform(center_array)  # 如果属性数量大于2，降维
    else:
        dataset = array(dataset)
    # 做散点图
    label = array(labels)
    plt.scatter(dataset[:, 0], dataset[:, 1], marker='o', c='black', s=7)  # 原图
    # plt.show()
    colors = np.array(
        ["#FF0000", "#0000FF", "#00FF00", "#FFFF00", "#00FFFF", "#FF00FF", "#800000", "#008000", "#000080", "#808000",
         "#800080", "#008080", "#444444", "#FFD700", "#008080"])
    # 循换打印k个簇，每个簇使用不同的颜色
    for i in range(k):
        plt.scatter(dataset[nonzero(label == i), 0], dataset[nonzero(label == i), 1], c=colors[i], s=7, marker='o')
    # plt.scatter(center_array[:, 0], center_array[:, 1], marker='x', color='m', s=30)  # 聚类中心
    plt.show()

if __name__ == "__main__":
    k = 3  # 聚类簇数
    T = 100  # 最大迭代数
    n = len(dataset)  # 样本数
    epsilon = 1e-5
    # 预测全部数据
    labels, centers = k_means(np.array(dataset), k, T, epsilon)
    F_measure, ACC, NMI, RI, ARI = clustering_indicators(original_labels, labels)  # 计算聚类指标
    print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI, "ARI", ARI)
　　 draw_cluster(dataset, centers, labels=labels)