异常检测：3西格玛原则

3σ原则基于正态分布的数学原理，它假设一组检测数据中只含有随机误差，通过计算得到标准偏差σ，然后按一定概率确定一个区间，对于超过这个区间的误差，就不属于随机误差而是粗大误差，将含有粗大误差的数据进行剔除。

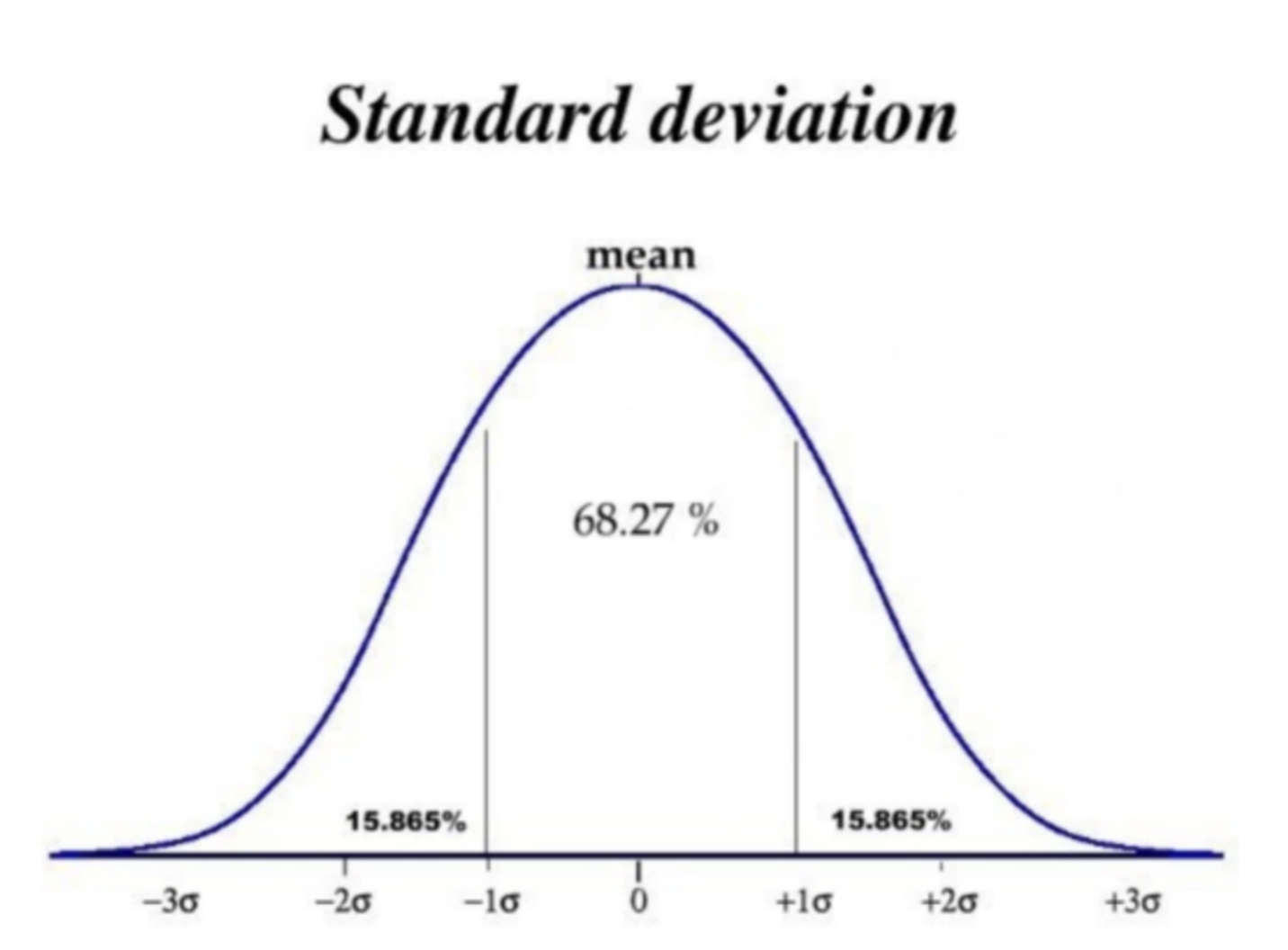
在统计学中，如果一个变量服从正态分布，且它的均值是u, 标准差是σ，那么将有：

（1）68.27%的数据会落在 u ± σ 内，即数据分布在处于(u−σ, u+σ)中的概率是0.6827

（2）95.45%的数据会落在 u ± 2σ 内，即数据分布在处于(u−2σ, u+2σ)中的概率是0.9545

（3）99.73%的数据会落在 u ± 3σ 内，即数据分布在处于(u−3σ, u+3σ)中的概率是0.9973

通常认为，数据“Y”的取值几乎全部集中在（μ-3σ,μ+3σ)区间内，超出这个范围的可能性仅占不到0.3%，这些超出该范围的数据可以认为是异常值。

 

 

代码实现：

import numpy as np  
import matplotlib.pyplot as plt  
from scipy.stats import lognorm  
import pandas as pd

# 设置参数  
s = 0.5  # 形状参数（σ），较小的值会导致更重的右尾  
mean = 0  # 对数正态分布的底数（μ）对应的对数均值  
scale = np.exp(s**2)  # 尺度参数（exp(σ^2)），确保对数正态分布的方差正确  
n_samples = 1000  # 样本数量  
  
# 生成对数正态分布数据  
data = lognorm.rvs(s=s, scale=scale, size=n_samples)  

# 写入excel
df = pd.DataFrame(data)
df.to_excel("data.xlsx", index=False, header=None)
 
# 绘制直方图  
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')  
  
# 绘制对数正态分布曲线作为参考  
xmin, xmax = plt.xlim()  
x = np.linspace(xmin, xmax, 100)  
pdf_values = lognorm.pdf(x, s=s, scale=scale)  
plt.plot(x, pdf_values, 'k', linewidth=2, label='Lognormal Distribution (s={})'.format(s))  
  
# 设置图表标题和坐标轴标签  
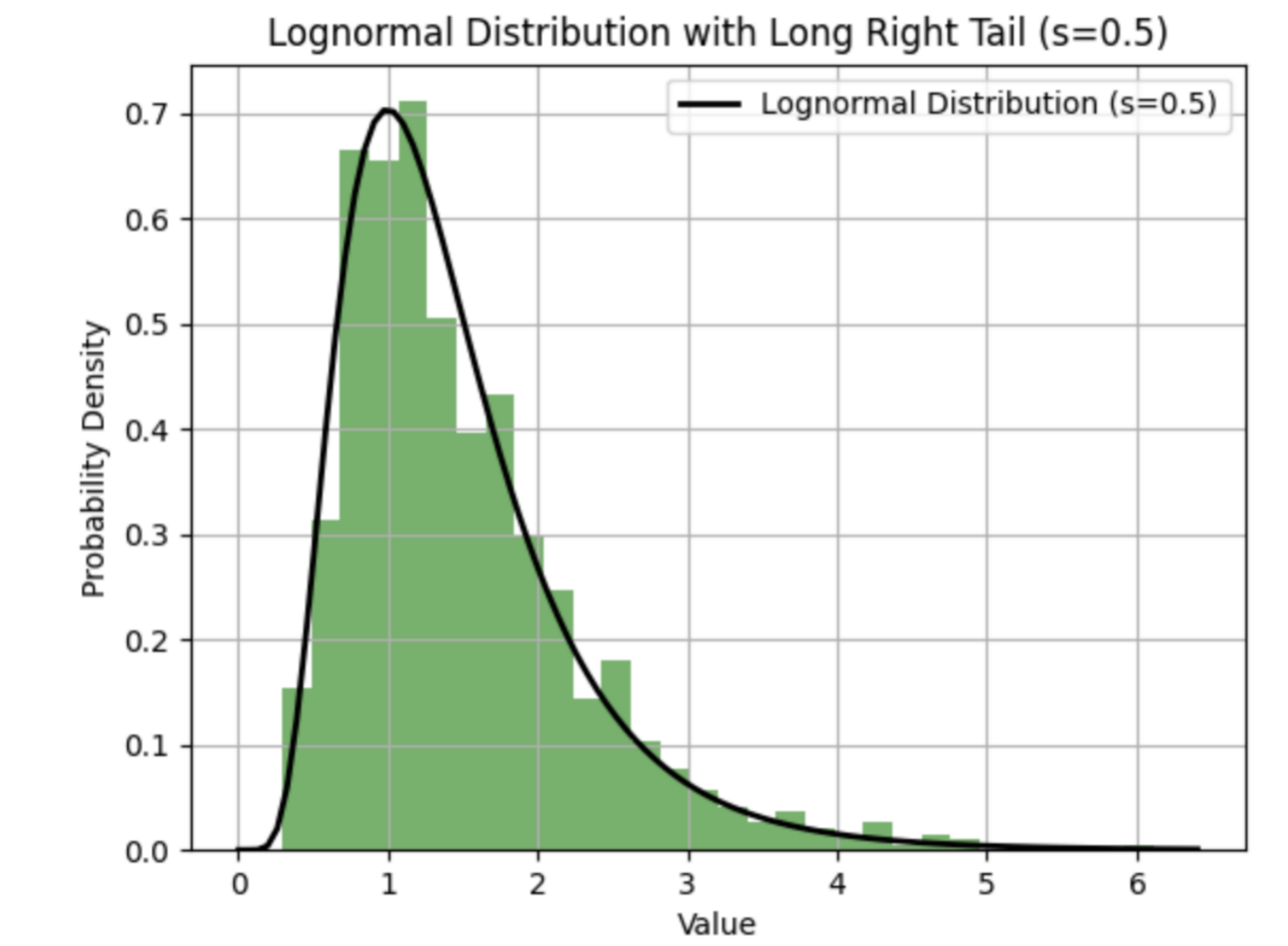
plt.title('Lognormal Distribution with Long Right Tail (s={})'.format(s))  
plt.xlabel('Value')  
plt.ylabel('Probability Density')  
plt.legend()  
  
# 显示图形  
plt.grid(True)  
plt.show()

 

3σ原则优缺点：

1、3σ原则的优点

1.简单易懂：3σ原则基于标准差的观念，提供了一个直观且易于理解的判断标准。通过计算数据的平均值和标准差，并与3σ进行比较，可以快速判断数据是否处于正常范围内。

2.科学性和客观性：由于3σ原则基于统计学原理，其判断具有一定的科学性和客观性。它依赖于数据的统计特性，而不是主观的、经验性的判断。

3.有效检测异常值：根据正态分布的特性，大约有99.73%的数据落在u±3σ范围内。因此，当一个数据点落在这一范围之外时，可以初步判断为异常值。

2、3σ原则的缺点

1.对样本量的依赖：3σ原则的有效性依赖于样本量的大小。当样本量较小时，使用3σ原则进行异常值检测可能不够可靠。因为小样本数据可能无法准确反映总体的分布特性。

2.对非正态分布数据的限制：3σ原则主要适用于具有正态分布或近似正态分布特性的数据。对于非正态分布的数据，3σ原则可能无法有效检测异常值，甚至可能出现误判。