异常检测：四分位距法（IQR）

一、IQR介绍

IQR（Interquartile Range）算法是一种用于检测异常值的统计方法，主要基于数据的四分位数。IQR 代表数据集中第 1 四分位数（Q1）和第 3 四分位数（Q3）之间的范围。

1.1 IQR 算法步骤

1）计算四分位数：

Q1（下四分位数）：数据中 25% 的值。
Q3（上四分位数）：数据中 75% 的值。

2）计算 IQR：

𝐼𝑄𝑅=𝑄3−𝑄1

3）定义异常值的边界：

下限=𝑄1−1.5×𝐼𝑄𝑅
上限=𝑄3+1.5×𝐼𝑄𝑅

4）检测异常值：

任何小于下限或大于上限的数据点都被视为异常值。

1.2 IQR实例

假设有以下数据集： 8,10,12,14,15,16,18,20,22,25,30,50,100

计算步骤如下：

1）排序数据

8,10,12,14,15,16,18,20,22,25,30,50,100

2）计算 Q1 和 Q3

Q1（下四分位数）：14（取第4个数，它前面有3个数，后面有9个数）

Q3（上四分位数）：25（取第10个数，它前面有9个数，后面有3个数）

3）计算 IQR

𝐼𝑄𝑅=𝑄3−𝑄1=25−14=11

4）定义异常值边界

下限： 𝐿𝑜𝑤𝑒𝑟𝐵𝑜𝑢𝑛𝑑=𝑄1−1.5×𝐼𝑄𝑅=14−1.5×11=−2.5

上限： 𝑈𝑝𝑝𝑒𝑟𝐵𝑜𝑢𝑛𝑑=𝑄3+1.5×𝐼𝑄𝑅=25+1.5×11=41.5

5）检测异常值

数据集中小于 -2.5 或大于 41.5 的值，在这个数据集中，异常值是 50 和 100。

二、python实例

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 创建包含异常值的数据
data = [8, 10, 12, 14, 15, 16, 18, 20, 22, 25, 30, 50, 100]

# 将数据转换为 Pandas DataFrame
df = pd.DataFrame(data, columns=['Scores'])

# 计算 Q1 和 Q3
Q1 = df['Scores'].quantile(0.25)
Q2 = df['Scores'].quantile(0.5)
Q3 = df['Scores'].quantile(0.75)
IQR = Q3 - Q1

# 计算上下限
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 检测异常值
outliers = df[(df['Scores'] < lower_bound) | (df['Scores'] > upper_bound)]

# 打印结果
print(f"Q1: {Q1}, Q2: {Q2}, Q3: {Q3}, IQR: {IQR}")
print(f"Lower Bound: {lower_bound}, Upper Bound: {upper_bound}")
print(f"Outliers: {outliers['Scores'].values}")

# 绘制箱线图
plt.figure(figsize=(10, 6))
sns.boxplot(data=df['Scores'])
plt.title('Boxplot of Scores with Outliers')
plt.ylabel('Scores')

# 添加 lower_bound 和 upper_bound 的水平线
plt.axhline(y=lower_bound, color='red', linestyle='--', label='Lower Bound (Q1 - 1.5 * IQR)')
plt.axhline(y=upper_bound, color='blue', linestyle='--', label='Upper Bound (Q3 + 1.5 * IQR)')

# 添加图例
plt.legend()

# 显示图形
plt.show()

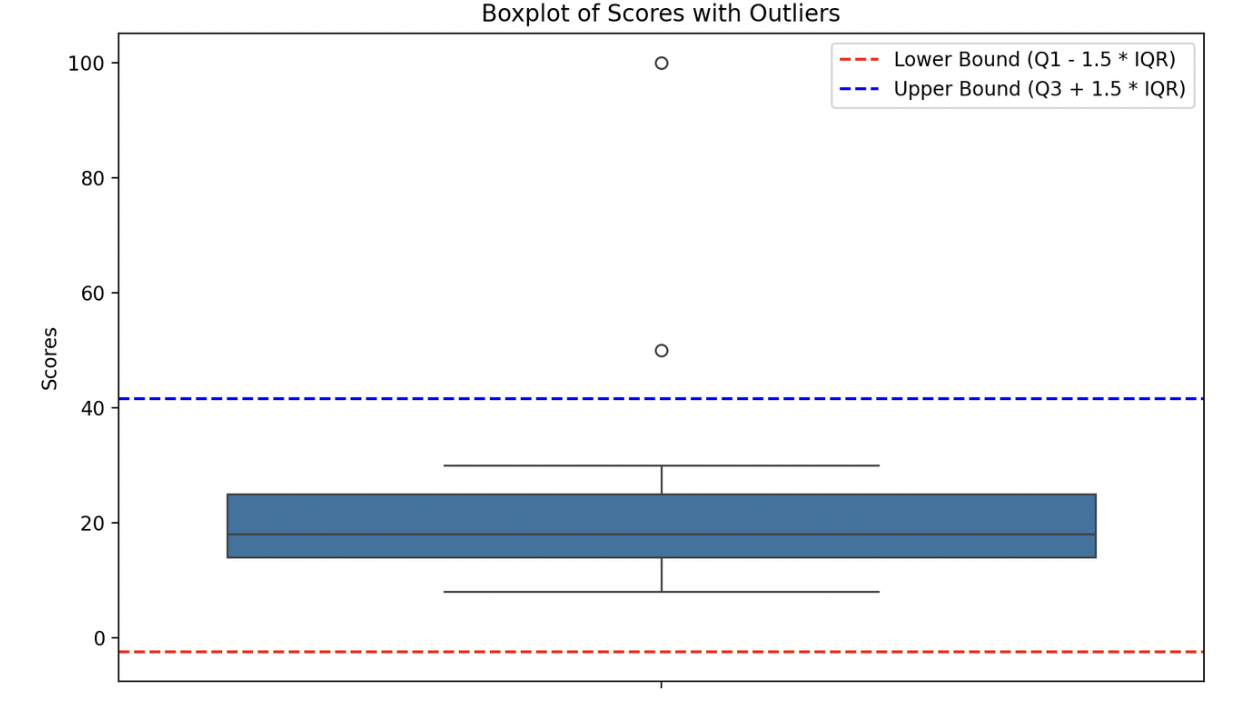
执行结果：

Q1: 14.0, Q2: 18.0, Q3: 25.0, IQR: 11.0
Lower Bound: -2.5, Upper Bound: 41.5
Outliers: [ 50 100]

 

参考书籍：