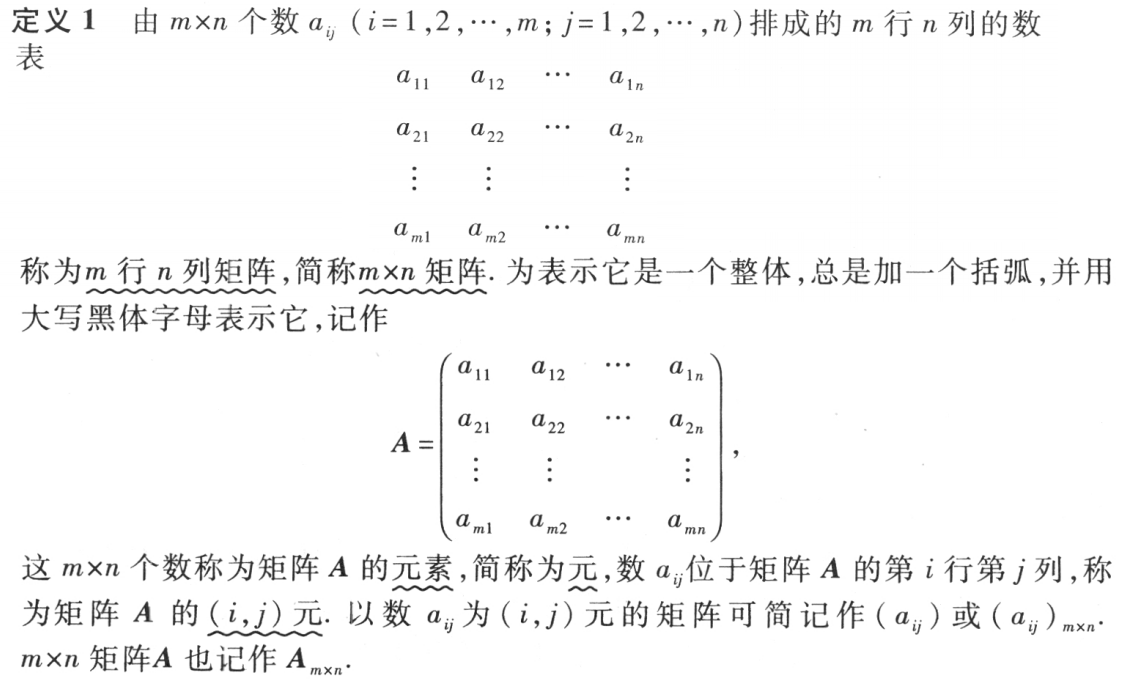
矩阵的定义

 

实矩阵和复矩阵 

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵

n 阶矩阵或n 阶方阵

行数与列数都等于 n 的矩阵称为n 阶矩阵或n 阶方阵. n 阶矩阵 A 也记作 A _n.

行矩阵和行向量

只有一行的矩阵 A =（a1 a2… an），称为行矩阵，又称行向量

为避免元素间的混淆，行矩阵也记作 A =（a1，a2，…，an）.

列矩阵，又称列向量

只有一列的矩阵

 

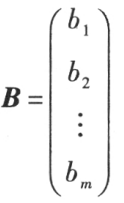
 同型矩阵

两个矩阵的行数相等、列数也相等时，就称它们是同型矩阵

对角矩阵 

对应 阶方阵

 

这个方阵的特点是：从左上角到右下角的直线（叫做对角线）以外的元素都 是 0.这种方阵称为对角矩阵，简称对角阵.对角阵也记作 A = diag（λ1，λ2，…，λn）；