背包问题

背包问题

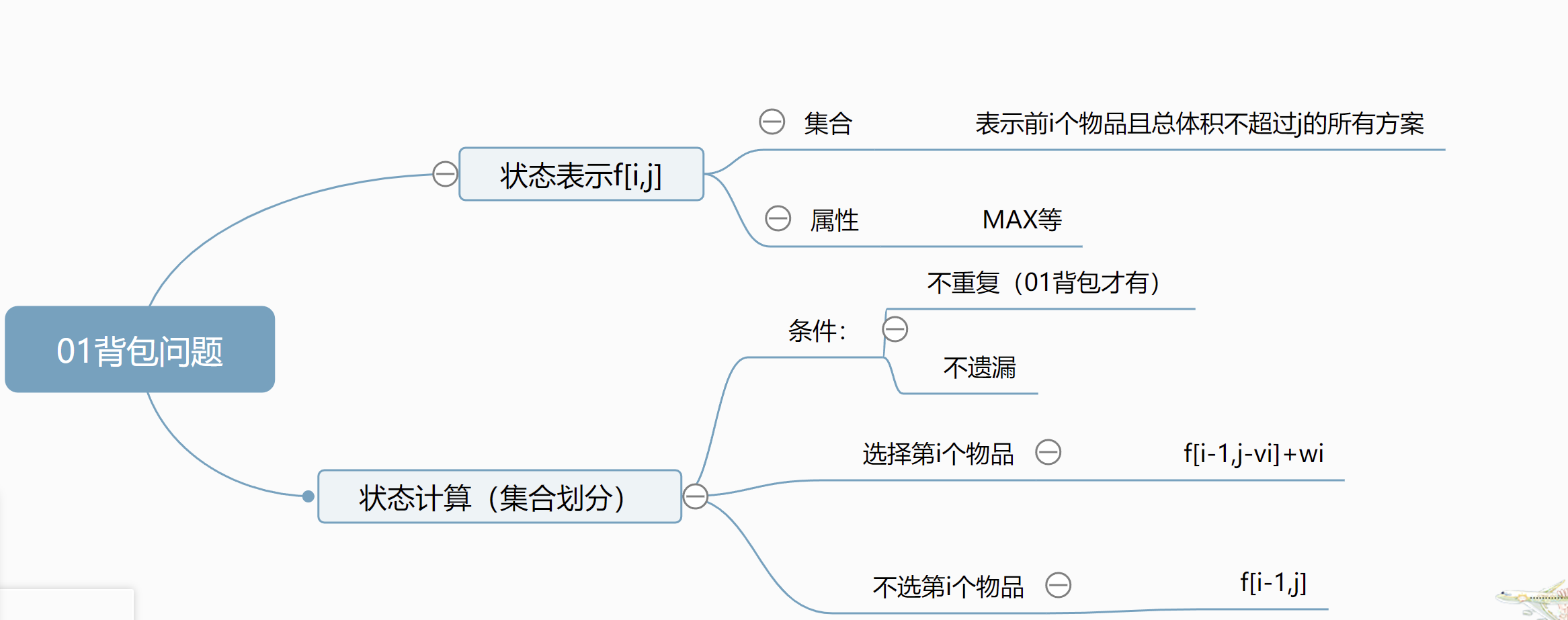
01背包问题

n个物品，每个物品的体积是vi，价值是wi，背包的容量是j
若每个物品最多只能装一个，且不能超过背包容量，则背包的最大价值是多少？

int n;			//物品数量
int m;			//背包容量
int v[N];		//体积
int w[N];		//价值

//二维朴素版本
int f[N][M];
for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
        if(j<v[i]) f[i][j]=f[i-1][j];
		else f[i][j]=max(f[i-1][j],f[i-1,j-v[i]]+w[i])
cout<<f[n][m]

//一维版本
int f[M];
for(int i=1;i<=m;i++)
    for(int j=m;j>=v[i];j--)//注意是倒序，否则写后读
        f[j]=max(f[j],f[j-v[i]]+w[i])
cout<<f[m]

    二维压缩成一维，实际上是寻找避开写后读错误的方法：
	由于f[i][j]始终只用上一行的数据f[i-1][...]更新（迭代更新的基础，如果还需用上上行数据则不可压缩）
	且f[i][j]始终用靠左边的数据f[i-1][<=j]更新（决定了只能倒序更新）




	举例说明：
	二维：dp[3][8] = max(dp[2][8], dp[2][3] + w[3])   此时的dp[2][8]和dp[2][3]都是上一轮的状态值
	
	一维：dp[8] = max(dp[8], dp[3] + w[3])      我们要保证dp[8]和dp[3]都是上一轮的状态值
	
	按照逆序的顺序，一维dp数组的更新顺序为：dp[8], dp[7], dp[6], ... , dp[3]
	
	也就是说，在本轮更新的值，不会影响本轮中其他未更新的值！较小的index对应的状态是上一轮的状态值！
	
	如果按照顺序进行更新，dp[3] = max(dp[3], dp[0] + w[0])，对dp[3]的状态进行了更新，那么在更新dp[8]时，用到的dp[3]
	就不是上一轮的状态了，不满足动态规划的要求。
	例子来自链接：https://www.acwing.com/file_system/file/content/whole/index/content/2978/

完全背包问题

每个物品可以取任意个

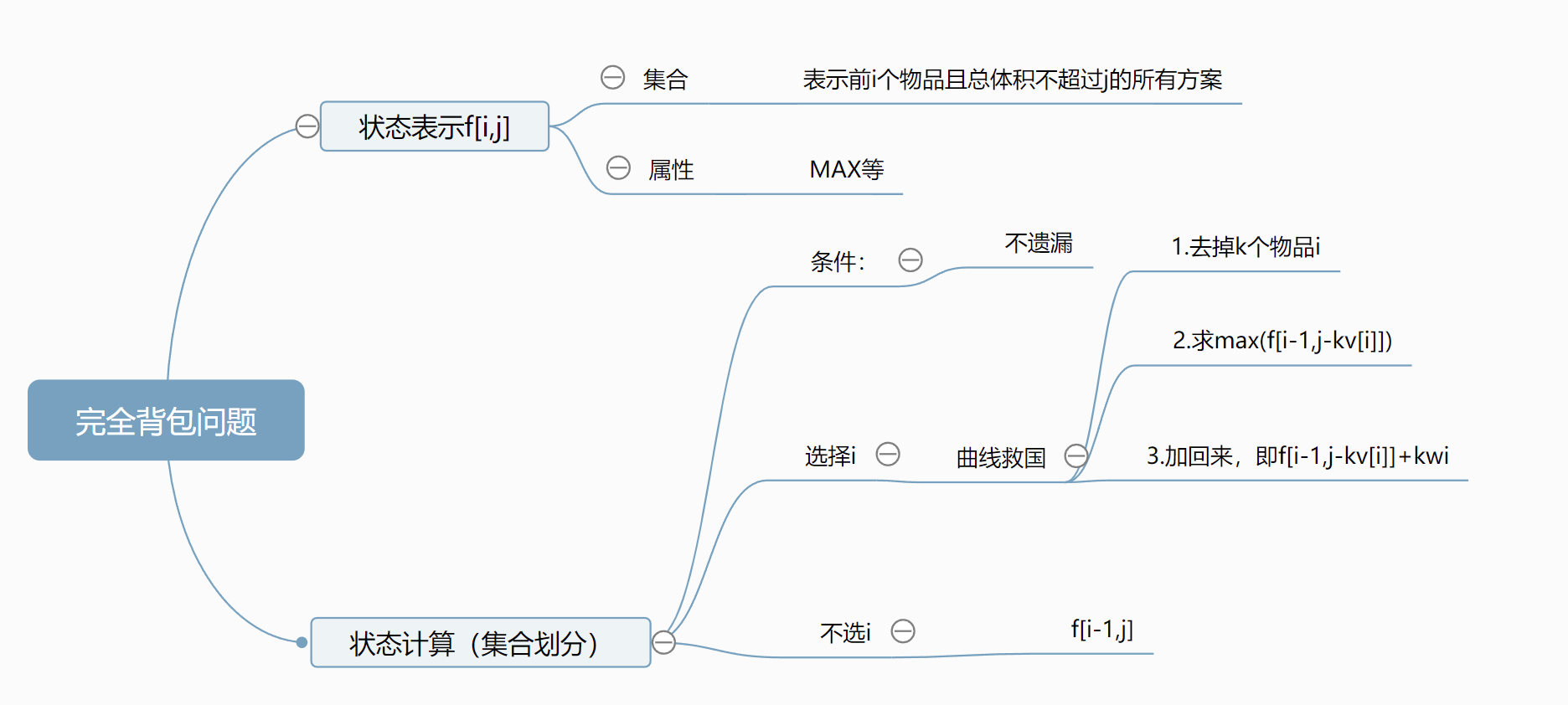
假设背包容量为jj时，最多可装入k个物品i，则有

$$f(i,j)=max{f(i−1,j),f(i−1,j−vi)+wi,f(i−1,j−2vi)+2wi,⋯,f(i−1,j−kvi)+kwi}$$

考虑

$$f(i,j−vi)=max{f(i−1,j−vi),f(i−1,j−2vi)+wi,f(i−1,j−3vi)+2wi,⋯,f(i−1,j−kvi)+(k−1)wi}$$

上式变形得

$$f(i,j−vi)+wi=max{f(i−1,j−vi)+w,f(i−1,j−2vi)+2wi,f(i−1,j−3vi)+3wi,⋯,f(i−1,j−kvi)+kwi}$$

综上可得

$$f(i,j)=max{f(i−1,j),f(i,j−vi)+wi}$$

//二维形式
int f[N][M];    // f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i) 
    for(int j = 1; j <= m; ++j)
        if(j < v[i]) f[i][j] = f[i-1][j];   //  当前重量装不进，价值等于前i-1个物品   
        else f[i][j] = max(f[i-1][j], f[i][j-v[i]] + w[i]); // 能装，需判断  
cout << f[n][m];

// ---------------一维形式---------------
int f[M];   // f[j]表示背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i) 
    for(int j = v[i]; j <= m; ++j)//正序
        f[j] = max(f[j], f[j - v[i]] + w[i]);          
cout << f[m];           // 注意是m不是n

形式上和01背包差不多，在二维数组表示下，主要差别在:
	在选择第i物品时，用的是f[i][j-v]+w，而不是f[i-1][j-v]+w
	上述条件决定了在每次迭代时，必须正向遍历，而不是反向遍历
在一维数组表示下，主要差别只表现为迭代的顺序（正向或反向）
在一维数组表示下，01背包只能反向是因为它主要用到上一行的数据来更新当前行数据，如果正向遍历，则会修改上一行的数据，出现写后读错误；完全背包只能正向是因为它需要用到当前行的数据更新，如果反向遍历，使用的是上一行的数据，则不符合公式

多重背包问题

第i个物品至多拿si件

$$f(i,j)=max{f(i−1,j),f(i−1,j−vi)+wi,f(i−1,j−2vi)+2wi,⋯,f(i−1,j−sivi)+siwi}$$

而

$$f(i,j−vi)=max{f(i−1,j−vi),f(i−1,j−2vi)+wi,f(i−1,j−3vi)+2wi,⋯,f(i−1,j−sivi)+(si−1)wi,f(i−1,j−(si+1)vi)+siwi}$$

变形后得

$$f(i,j−vi)+wi=max{f(i−1,j−vi)+wi,f(i−1,j−2vi)+2wi,f(i−1,j−3vi)+3wi,⋯,f(i−1,j−sivi)+siwi,f(i−1,j−(si+1)vi)+(si+1)wi}$$

多了一项

$$f(i−1,j−(si+1)vi)+(si+1)wif(i−1,j−(si+1)vi)+(si+1)wi$$

因此无法按照完全背包的方式优化

二进制优化

已知$1,2,4,⋯,2^k$可以由系数0和1线性组合出$0-2^{k+1}−1$。考虑更一般的情况，若想线性组合出$0- S，S<2{k+2}$，则猜测可由$1,2,4,⋯,2^k,C$组合出，其中$C<2k+1$，显然，在C一定存在的情况下，可得到的数的范围为C-S。由于$C<2k+1$，则$C≤2^{k+1}−1$，故$[0,2^{k+1}−1]∪[C,S]⊇[0,2^{k+1}−1]∪[2^{k+1}−1,S]=[0,S]$，即可用$1,2,4,⋯,2k,C$表示任何$<2k+2$的数
因此对于有s[i]件的某个物品i，可以打包成$⌈log⁡s[i]⌉$个物品，每包有1,2,4,⋯,2k,C件物品i，其中$k=⌈log⁡s[i]⌉-1$

// -----------------未优化（完全背包模板）----------------------
int f[N][M];    // f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
        for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
            f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);

// -----------------------二进制优化---------------------------
// 读入物品个数时顺便打包,a,b,s 为体积价值数量
int k = 1;      // 当前包裹大小
int cnt=0;
while (k <= s)
{
    cnt ++ ;            // 实际物品种数
    v[cnt] = a * k;
    w[cnt] = b * k;
    s -= k;
    k *= 2;             // 倍增包裹大小
}
if (s > 0)
{
    // 不足的单独放一个，即C
    cnt ++ ;
    v[cnt] = a * s;
    w[cnt] = b * s;
}
n = cnt;        // 更新物品种数

// 转换成01背包问题
for (int i = 1; i <= n; i ++ )
    for (int j = m; j >= v[i]; j -- )
        f[j] = max(f[j], f[j - v[i]] + w[i]);

cout << f[m] << endl;

用二进制优化后，注意物品种数变成N×logMN×log⁡M，问题转换成01背包问题
时间复杂度为O(nmlogs)

分组背包问题

每组物品中至多拿1个

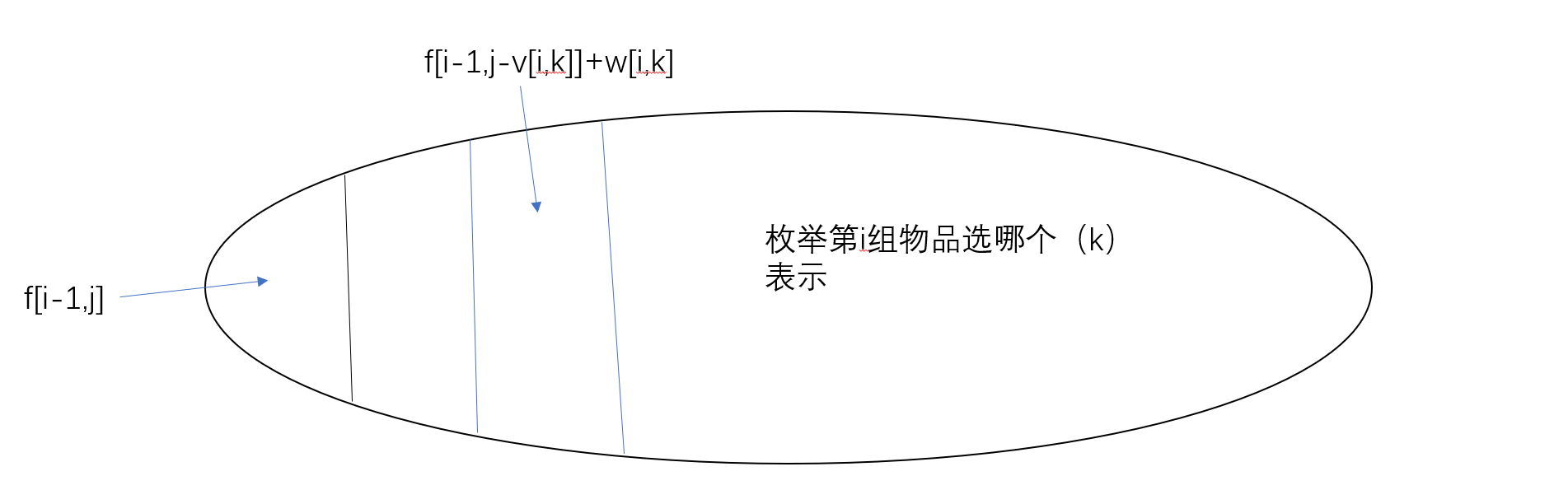
实际上是带有约束的01背包问题，状态计算为

$$f(i,j)=max{f(i−1,j),f(i−1,j−v(i,k))+w(i,k)}$$

解法：

int n;              // 物品总数
int m;              // 背包容量
int v[N][S];         // 重量 
int w[N][S];         // 价值
int s[N];           // 各组物品种数

 for (int i = 1; i <= n; i ++ )
 {
     cin >> s[i];
     for (int j = 1; j <= s[i]; j ++ )
         cin >> v[i][j] >> w[i][j];
 }

// 处理数据
for (int i = 1; i <= n; i ++ )
    for (int j = m; j >= 1; j -- )
        for (int k = 1; k <= s[i]; k ++ )
            if (v[i][k] <= j)
                f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

cout << f[m] << endl;