回溯法和动态规划的一般模板

1.回溯法

回溯法的基础题目类型就是子集树和排列树，掌握最基础的模板，那么其它的题目都可以在此上变形得到，子集树即如下图所示：

 

 

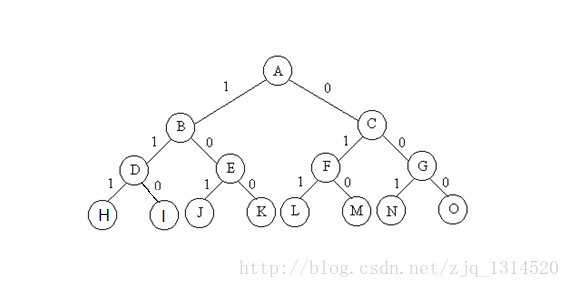
 同一个元素不能被选入多次，子集树的算法模板为

void Backtrack(int t) {     //t 表示当前是树的第t层，即对集合 S 中的第 t 个元素进行判断
    if (t > n)
        output(x);          //大于S中总的元素个数 ，遍历完成 
    else
        for (int i = 0; i < = l; i++) {     // 两种可能 加入或者不加入到解集合 
            x[t] = i;
            if (Constraint(t) && Bound(t)){     //满足约束条件  
                    Backtrack(t + 1);           //对 t+1 层进行判断 
                }
        }
}

还有就是排列树，排列树即

 

 

 这种，即一个元素可以多次被选择，排列树的模板为

void Backtrack(int t) {     //t 表示集合 S 的第 t 个元素 
    if (t > n)
        output(x);
    else
        for (int i = t; i <= n; i++) {      //第t 个元素与其后面的所有元素进行交换位置 
            swap(x[t], x[i]);
            if (constraint(t) && bound(t)){ 
                    backtrack(t + 1);
                }
            swap(x[t], x[i]);
        }
}

在回溯法的问题中，只要在这两种基础的模板上变形即可。当然回溯法的应用也有很多变形，但要抓住的是一般回溯的策略都是在遍历一个树，要多想想这到底是一个怎么样的树，怎么样遍历它，即了解其递归树，根据其递归树写算法。常见的变形有如要求同层去重、求一个集合的幂集等。

2.动态规划

动态规划问题相对来说有一点难度，这里可以帮助给出动态规划的一般思路：

首先确定问题符合动态规划问题的一般条件，即无后效性、最优子结构性质和重叠子问题性质。一般我们可以这样理解，如果你想构造一个一维或二维dp数组，如果当前要决策的变量dp[i]的值跟后面的决策无关(无后效性)，仅仅和前面的某个或者某几个dp[j](其中j为小于i的值)有关，且dp[j]也是之前第j个决策变量决策时的最优选择(最优子结构性质)，同时由决策dp[j]时的状态转移到dp[i]的状态的转移策略和dp[i]转移到dp[k](其中k大于i)的状态转移策略是相同的，那么这时候就适合用动态规划算法。而对于重叠子问题性质，可以这样理解，考虑该问题的暴力穷举解法，如果发现在穷举过程中发现后面几个计算都重复使用了前面某(几)种重复的过程，那么就可以考虑DP(或贪心)。其实DP的思想是和分治类似的，只不过DP利用了重叠子问题的性质，将之前保存的结果存储下来，这样就可以减少一部分计算量。

动态规划算法和贪心算法的不同之处在于，贪心算法往往只跟当前状态有关，而动态规划是不仅仅和当前状态有关，并且和之前的某些状态有关的。如果决策策略只和当前状态有关，那么这个问题一般适合应用贪心，而若决策策略和前面几个状态都有关系，那么可能适合于动态规划思想。

当遇到下一个要求的值（或序列）可以用递归求解前一个/几个状态的值得到时(如斐波那契数列)，考虑动态规划思想，因为动态规划就是对重复递归的优化。

当确定可以使用动态规划算法后，首先要确定这个dp数组的含义(状态定义)，即这个dp数组每一个元素代表着什么含义，一般的dp数组的每个元素就当前阶段目标的最优取值/最优状态；

思考这个动态规划中决策变量是什么，即可能的决策有哪些（x[i][j]，表示根据第j个阶段决策完后的状态state[j]能选择的最优决策方案x[i][j]）；考虑这个动态规划中每一个阶段决策前后状态发生了什么改变(change[i][j]，表示由第j个阶段决策完状态state[j]转换到第i个阶段决策完state[i]后状态的变化，即state[i]=state[j]+change[i][j]），决策前后处于什么状态（j个阶段决策后，i个阶段决策前state[j]，i个阶段决策后state[i]）；

动态规划每一步就是选取目前怎么决策(或者考虑当前最优策略可以由前面哪几个状态转移而来)，而当前阶段怎么样决策取决于之前某一个阶段的最优目标以及根据当时阶段决策完之后的状态选取最优决策之后产生的影响，但当前阶段可以由之前好几个阶段决策后的状态转换而来，也就是说，例如：既可以由前一个阶段决策完的状态state[i-1](即此时j = i-1)转换到当前决策完的状态state[i-1]+change[i][i-1]，假设我们的决策是x[i][i-1]，也可以由向前二个阶段决策完的状态state[i-2]转换而来到当前另一种当前最优决策完之后的状态state[i-2]+change[i][i-2]，而这时我们的决策是x[i][i-2]，而我们选择两者之中最优的，即state[i] = best(state[i-1]+change[i][i-1]，state[i-2]+change[i][i-2])。

按照下图，寻找状态转移方程就是寻找某个阶段i可能由哪些位置转换来，比如此图中j和k，那么j和k与i的关系是什么？j=f(i)，k=g(i)的f，g怎么确定。另外，由j处的state[j]到state[i]的转换change[i][j]是什么？

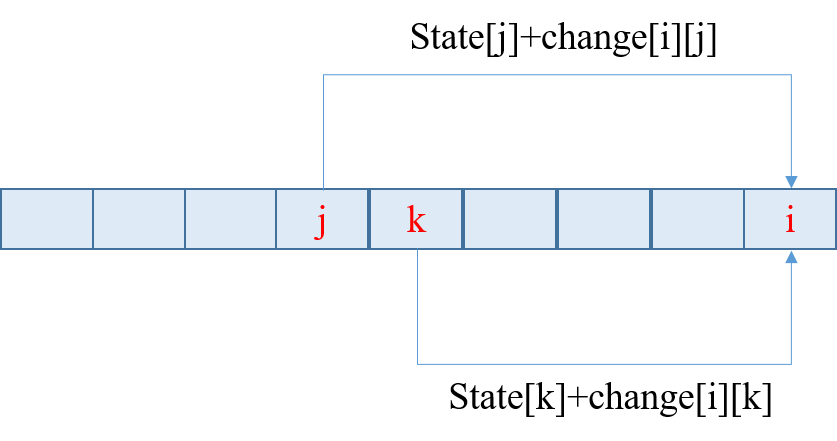
一般情况下，change[i][j]由x[i][j]和state[j]共同决定(多数情况下，state数组既保存最优的策略得到的目标，也保存着当前状态的信息，少数情况下state和最优策略目标值dp数组需要用不同的数组存储)，而x[i][j]一般由state[j]以及所给的数组option有关系，即你当前决策要根据当前状态state[j]和可选方案限制option共同决定。即change[i][j]=f(x[i][j]，state[j])=f(g(state(j)，option)，state[j])。

然后动态规划算法的最重要的就是提取状态转移方程，一个可以参考的做法是考虑当前决策可能在哪几个状态的基础上，和前面的哪些状态有关，即先找到dp[i]和dp[j]、dp[m]、dp[n]这些先前状态的位置，也即j、m、n可能的取值，然后要确定j，m，n怎么由i得到，比如j可能是i-1，m可能是i-2，n可能是i-dp[i-1]，此时已经确定dp[i]和哪些状态有关系了。接下来，就是确定怎么由dp[j]，dp[m]，dp[n]得到dp[i]，也就是状态转移方程，一般就是根据当时的状态dp[j]以及经过了几个阶段后的影响change[i][j]，然后求出每个有关的状态+影响，即dp[j]+change[i][j]，dp[m]+change[i][m]，以及dp[n]+change[i][n]多个取最优。

当对动态规划转移方程仍然不清晰时，可以手动采用表格法尝试一下模拟的过程。

动态规划的一般模板是

 1 int dynamicProgramming(int *option,int size)
 2 {
 3       int dp[size];
 4       dp[0] = initState;
 5       dp[1] = initState;     // 初始化边界
 6       for(int i = 2; i < size;++i)
 7       {
 8             int a = dp[i-1] + f(option[i],option[i-1] );
 9             int b = dp[i-2] + f(option[i],option[i-1] );
10             int c = dp[i-n] + f(option[i],option[i-n] );
11             dp[i] = best(a,b,c);
12       }
13       return dp[size-1];
14 }

当然这里给出的仅仅是最基本浅显的动态规划思路，动态规划的这种思想在很多重复递归的问题中都可以得到应用，因为动态规划的思想就是解决很多重复的递归，如斐波那契数列例子。看到有后几个阶段的结果需要重复前几个阶段所做的递归或前几个阶段所做的迭代时，就可以考虑动态规划。另外的有些变形的动态规划应用，还需要再多见识应用和总结。可以记忆一些经典的一维动规、二维动规的例子，遇到题目类比这些例子寻找思路。

动态规划找转移方程：表格法，类比相似题，从暴力遍历中逐步优化(存储那些重复计算过程的结果或者存储最优子问题目标)，使用状态转换图帮助寻找，以及递归子问题树方法。

递归子问题树的思路要求我们先将问题用(回溯)递归的方法解决问题(动态规划的问题是分治和递归的存储了重叠子问题结果的版本，因此动态规划问题都可以用递归来做)，比如以背包问题为例，其用递归的思路如下：

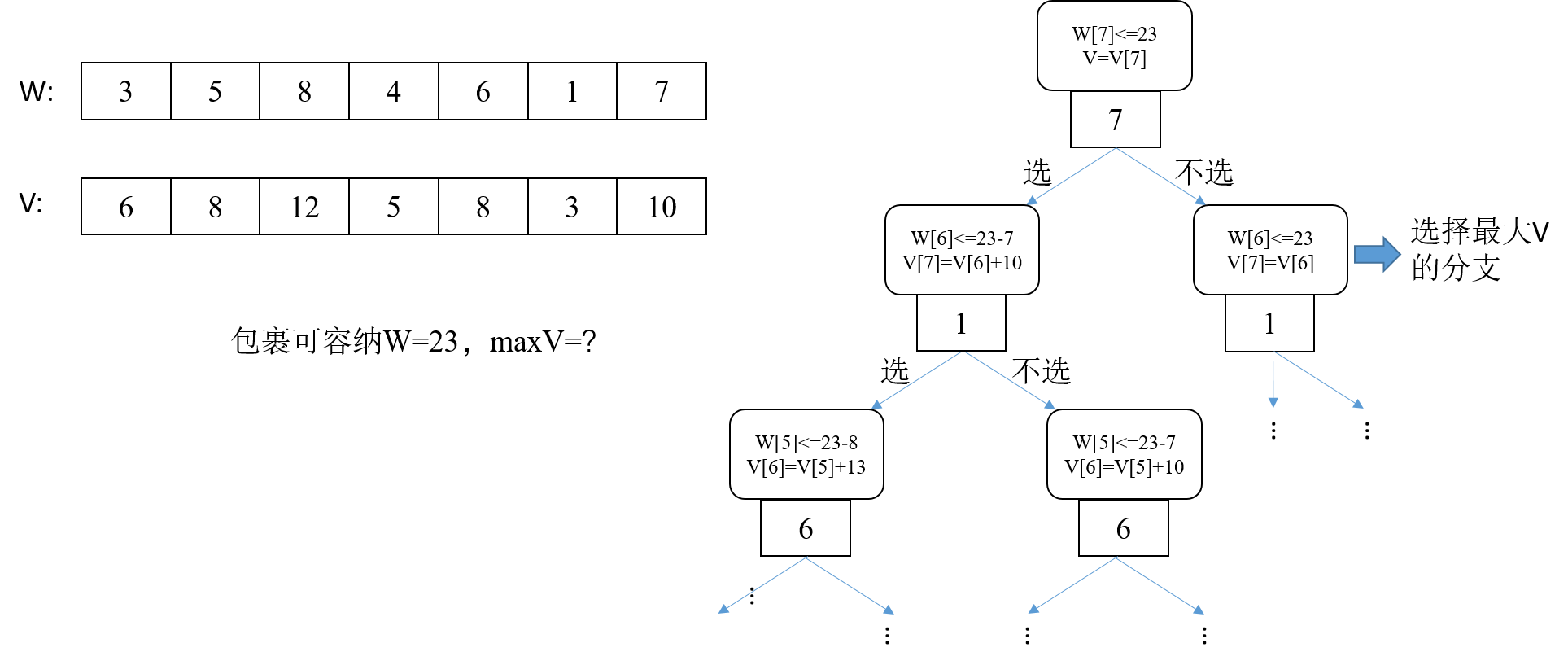
而对于使用递归方法解决问题，我们很容易写出其代码，接下来就是根据该递归子问题树找出重叠子问题。

于是我们可以子问题的形式获得dp数组的定义应为dp[n][W]，n为物品个数，W为不能超过的W值，而同时我们也可以根据子问题之间的状态转换得到状态转移方程为dp[i][j]=max(dp[i-1][j]，dp[i-1][j-W[i]]+V[i])。

也可以再结合表格法，以及状态转换图法进行辅助分析。总的来说思路是，先分解成一些重复子问题，而且重复子问题对下一级的重复子问题依赖结构相同(该子问题的最优目标只能是由下一级子问题的最优目标转换而来)，再定义状态(状态就是每一个子问题的最优目标)和状态转换(子问题和下一级子问题之间的关系)。重复子问题的寻找是核心。

动态规划 = 暴力 + 重复子问题优化。