TuringComplete闯关实录
游戏地址:Turing Complete
本游戏是基于一个强大的电路模拟器而开发的。这个电路模拟器允许你自由发挥想象力,以不同的解法通过各个关卡,或以自己喜欢的方式搭建属于自己的计算机。你可以随心所欲地在你的计算机上连接显示屏、计时器、声音元件等部件,也可以接收现实生活中的键盘和网络发送的数据。你甚至可以为你自己的计算机设计一套自己专属的汇编语言。
基础逻辑电路
与门
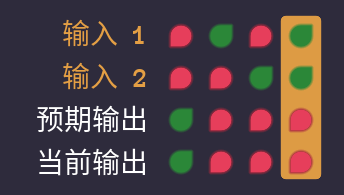
真值表:

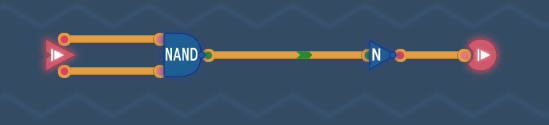
或非门
真值表:
推导:!(a or b) = !a and !b = !(!a nand !b)
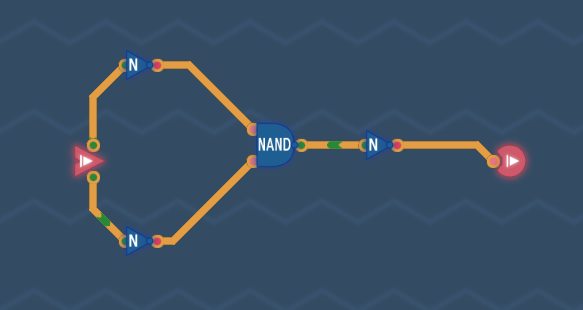
已有的与非门是只有ab都为0结果为1,要构建的或非门是只有ab都为1时结果为0,若先将ab的值取反送入与非门,就得到了一个跟或非门真值表完全相反的一个门电路,此时再加一个取反即可
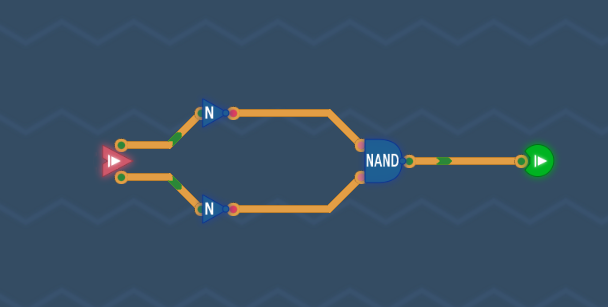
或门
真值表:

有了或非门的经验,立即就能得到一个或门:
高电平
目标:搭建一个始终输出高电平的电路
真值表:

分析:a or !a=1
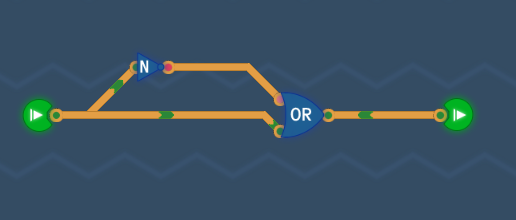
解锁词条:德摩根定律
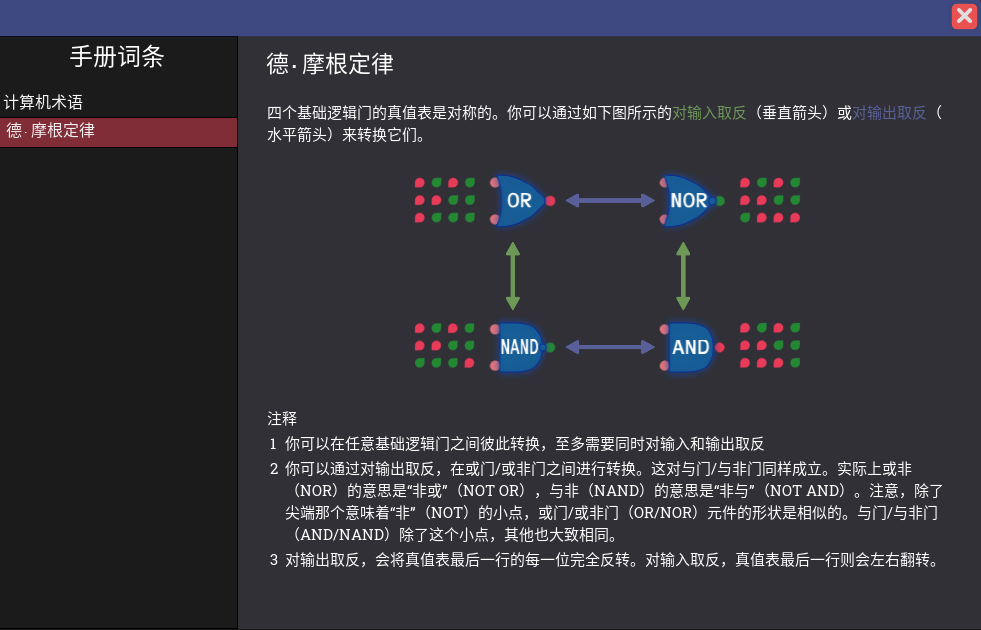
!(a or b)=a nor b!(a and b)=a nand b!a or !b = a nand b(!a and !b)=a nor b
比较有趣的是对输入取反,真值表的结果会倒序,注意图中or和nand中的输出列 |
| 
有了德摩根定律,回头再做一下之前的关卡很快
第二刻
目标:只有在第二刻为1的电路
真值表:

分析:只有当a=1,b=0时为1的电路,只需将a取反并和b一起放入与门
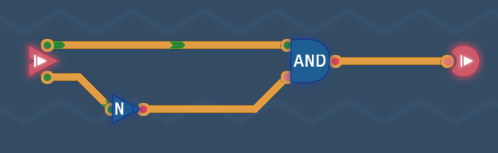
异或门
目标:在第二第三刻都输出1的电路,即不一样才为1的门(异或门)
真值表:

分析:!ab or !ba
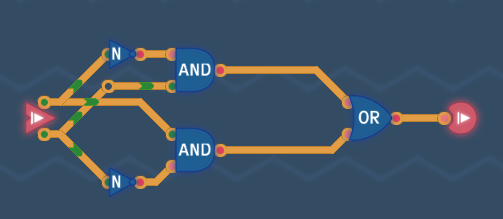
另一种思路:
目标真值表:
- 目标真值表:0110
- or真值表:0111
- nand真值表:1110
- 将二者输出and
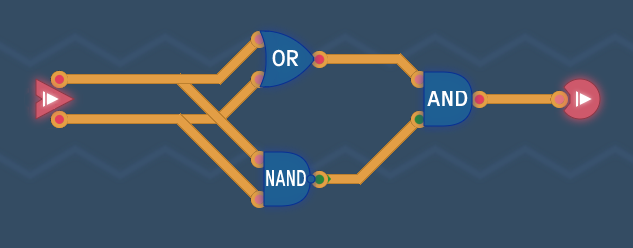
三路或门
真值表:

分析:a or b or c
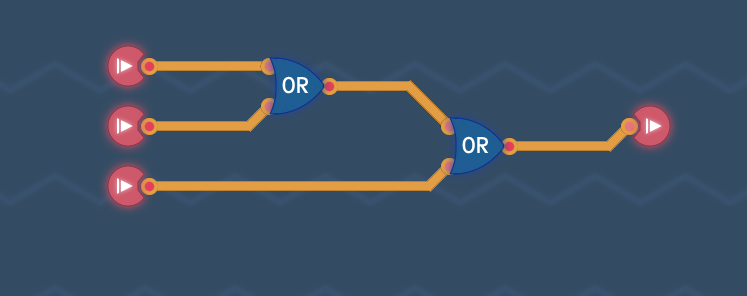
三路与门
真值表:

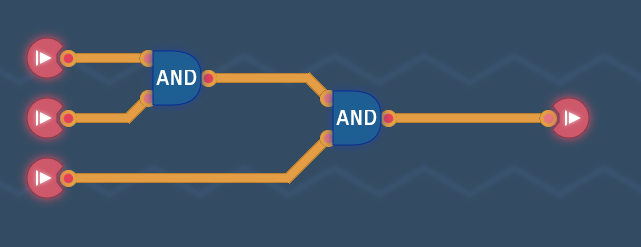
同或门
算数运算 & 存储器
成对的麻烦
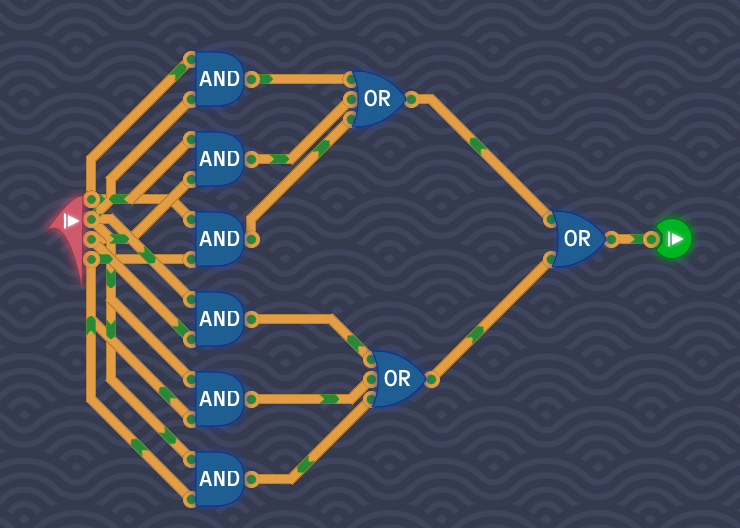
题目:四个输入中有两个或两个以上为1时,输出1
提示:别把这一关想的太复杂
真值表:

思路:令输入端为A、B、C、D,若输出1,则AB、AC、AD、BC、BD、CD中必然有至少一个为1(否则就无法构成两个或两个以上为1),让这些项相或即为结果
奇数个信号
题目:本关里你最多只能使用3个元件。只有当奇数个输入为1时才输出1。
真值表:

思考:令输入端为A、B、C、D,若A和B中不同时有奇数个1,则有全局有奇数个1。xor等价于两个输入中是否有奇数个1。所以结果为(A xor B) xor (C xor D)
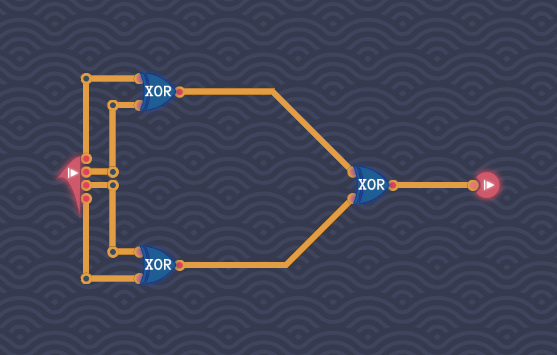
奇变偶不变
题目:输出01010101...(时钟!!!)

分析:使用延迟线将输出拉出一部分回馈到输入
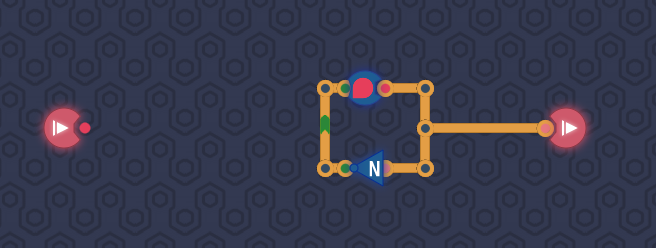
疑问:延迟线在真实电路中是什么?在真实电路中如何构建这样的时钟?
信号计数
题目:输入端4个,输出端3个,数出输入端中有几个1。把输出端看成一个二进制数,000~111对应0到7。
真值表:
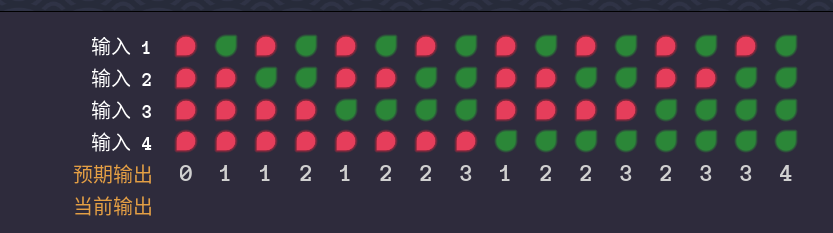
分析:
列出输入与输出的真值表

输出端口\(Y_2\)可以立即给出:\(Y_2=ABCD\)
对于\(Y_1\),只有当输入有2个或3个1时它为1,对于\(Y_0\),只有当有1个或3个1时,为1。很好解释,因为3这个数字需要\(Y_0\)和\(Y_1\)一起构成。
所以,\(Y_0\)就是题目——奇数个信号\(Y_0=(A xor B) xor (C xor D)\)
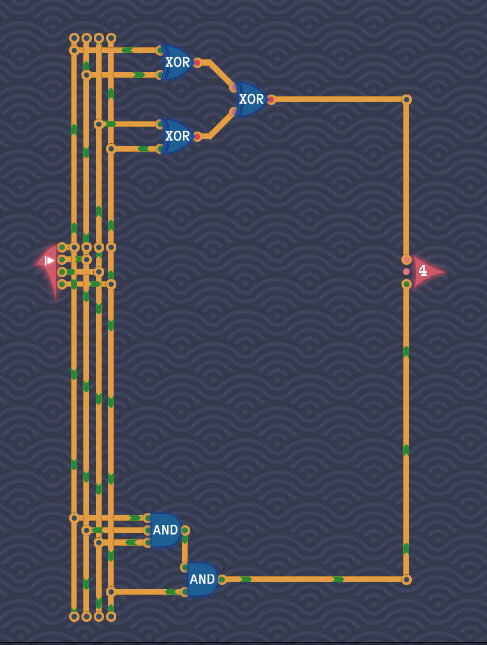
现在问题只剩解决\(Y_1\),在题目——成对的麻烦中,已经设计了一个2个或2个以上为1的电路,现在只需要在此基础上,想办法去掉四个输入都为1的情况即可
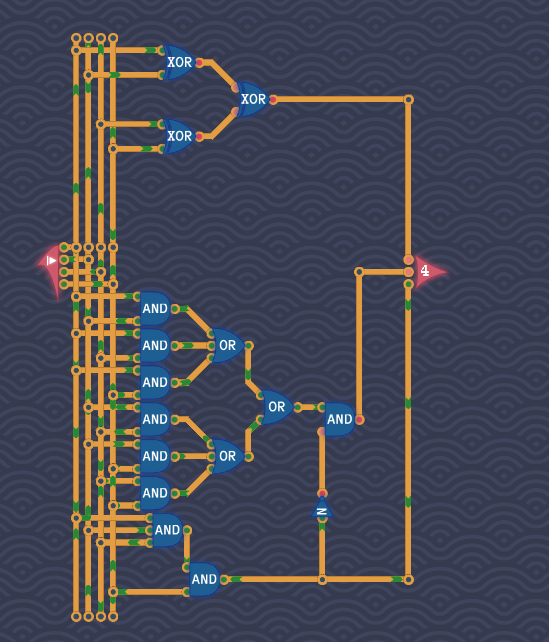
不得不说这里我们取巧了,应该可以通过设计把最后的AND和NOT门省掉,但是我真想不出来,但用逻辑代数化简的话总感觉不是自己想的没意思...先这样吧累了~~
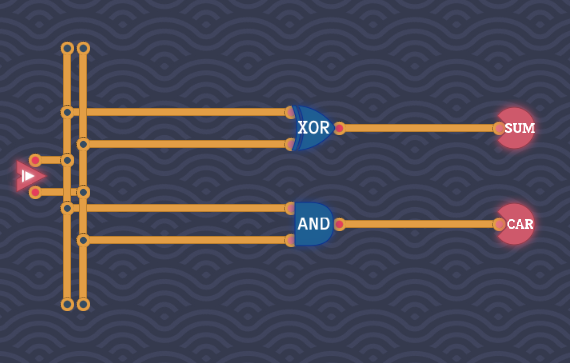
半加器
题目:输入两个1bit,输出一个1bit相加结果SUM,一个进位CAR
真值表:

分析:SUM=A xor B, CAR=A and B
加倍
题目:将输入的数值翻倍(输入数值在0~127),你有一个分线器将1byte拆分成8bit端口,一个集线器将8bit累加成1byte
分析:只需要将bit错位连接即可。

全加器
题目:输入三个1bit,输出一个1bit相加结果SUM,一个进位CAR
真值表:
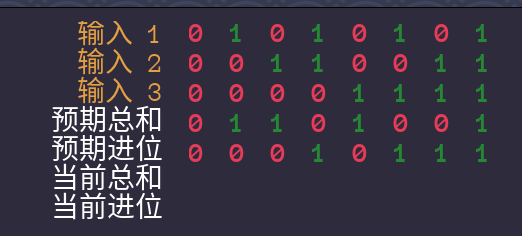
分析:CAR就是两个以上的时候才是1,SUM就是奇数个1的时候才是1,这俩电路我们都做过类似的。
\(CAR=AB+AC+BC\)
\(SUM=AxorBxorC\)
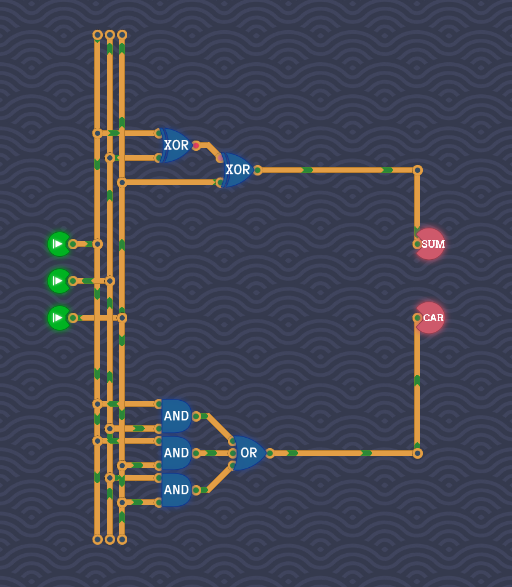
\(SUM\)的逻辑可以这样想,假设你有\(N\)个数,你需要判断\(N\)个数里是否有奇数个1,假设你已经得出了\(X\)为前\(M\)个数中是否有奇数个1(\(M<N\)),当\(X\)为真,你可以认为前\(M\)个数就是1个1,再和后面比较,不会改变全局的奇偶性;当\(X\)为假,你可以认为前\(M\)个数就是一个0,也不会改变全局的奇偶性。
我们已经知道判断两个数中是否有奇数个1,只需要一个异或门即可,那么两个异或门即可完成三个数中是否有奇数个1的判断。
更通用的,我们可以得出\(I_{i(i\in[0, n])}\)是否有奇数个1的逻辑表达式为\(I_0 xor I_1 xor I_2 xor ... xor I_n\)
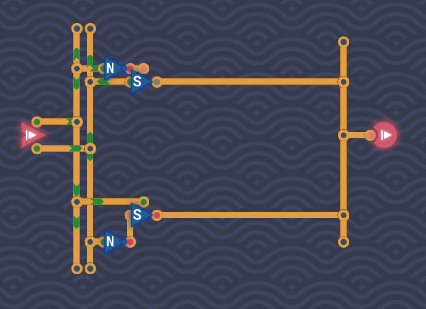
一位开关
题目:使用两个开关,两个非门构建一个异或门
组件——开关:
开关具有两个输入端,一个输出端,当两个输入端都为1时,输出端为1,否则,输出端被屏蔽。多个开关可以连接到同一根导线上,只要在任意时刻只有一个开关被激活即可。
八位加法器
题目:两个字节相加
分析:
我们能够利用的元件里已经有了一个三位的全加器,可以看作两位外加一个外部过来的进位相加,输出一个结果位,一个进位。

先让问题简单一些,考虑两个2bit A和B相加,A0代表A的第最低位,A1代表最高位,对于B也一样
A1 A0
B1 B0
很容易想出这样的电路将其累加最后得出O0、O1以及一个进位CAR1
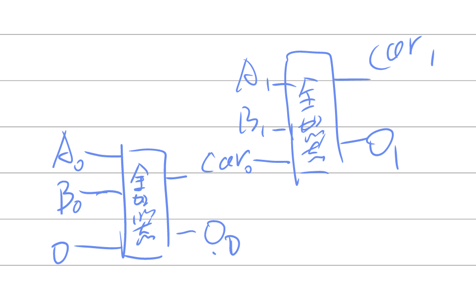
对于任意位数都是一样的:
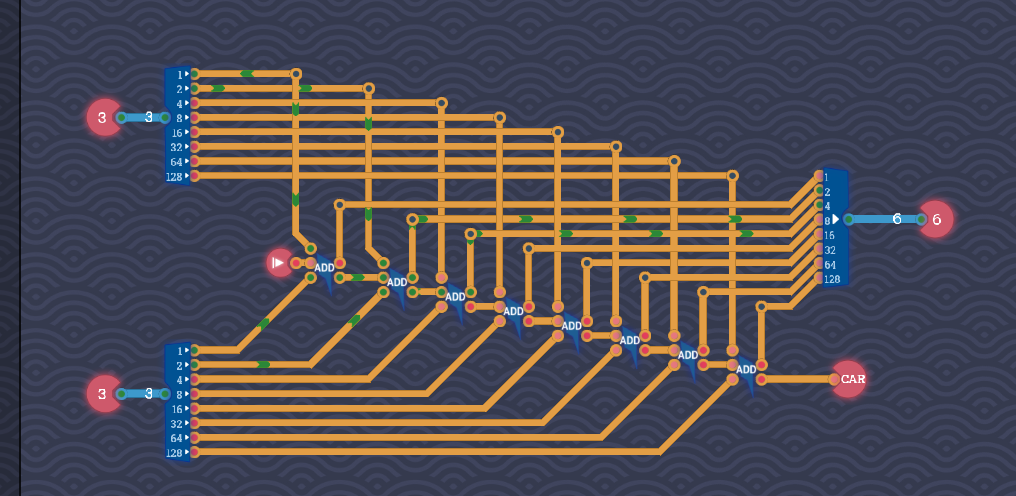
电路图丑点,但话糙理不糙是不是
数据选择器
题目:当选通输入(左侧最上)为0时,将A发送到输出端,否则将B发送到输出端,A和B都是一个字节

分析:还是先考虑简单情况,如果A和B不是字节,而是一位数字呢?
可以利用一位开关来完成SEL情况不同时传递不同的输入到输出上。
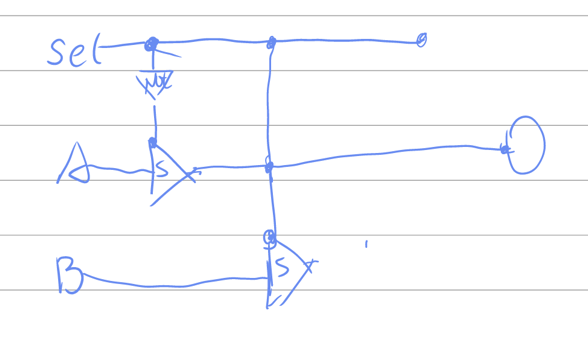
屎山,无力解释
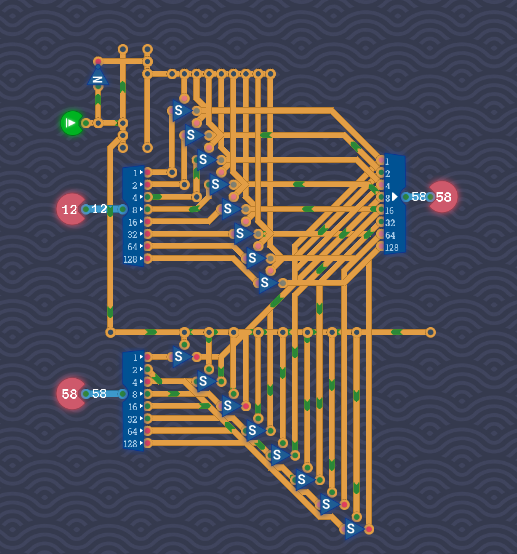
相反数
题目:输入一字节补码数,输出它的相反数。例:输入-1,输出1
分析:先降低难度,考虑三位补码数,将其真值表列出,可以发现不考虑100(4)和000(0),输出结果的绝对值刚好对称,且分界线两侧就是相反数。

接下来就是考虑如何让分界线上边的数映射到下边,其实就是取反后再加1。所以最后的电路是这样的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号