递归与递推

递归

把某一个问题分解成同种子问题。
求斐波那契数列前n项和。

代码

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;

//递归：递归树 
int f(int n){
	if (n == 1) return 1;
	if (n == 2) return 2;
	return f(n-1) + f(n-2);
}
int main()
{
 	int n;
	scanf("%d",&n);
	printf("%d",f(n));
	return 0;	
} 

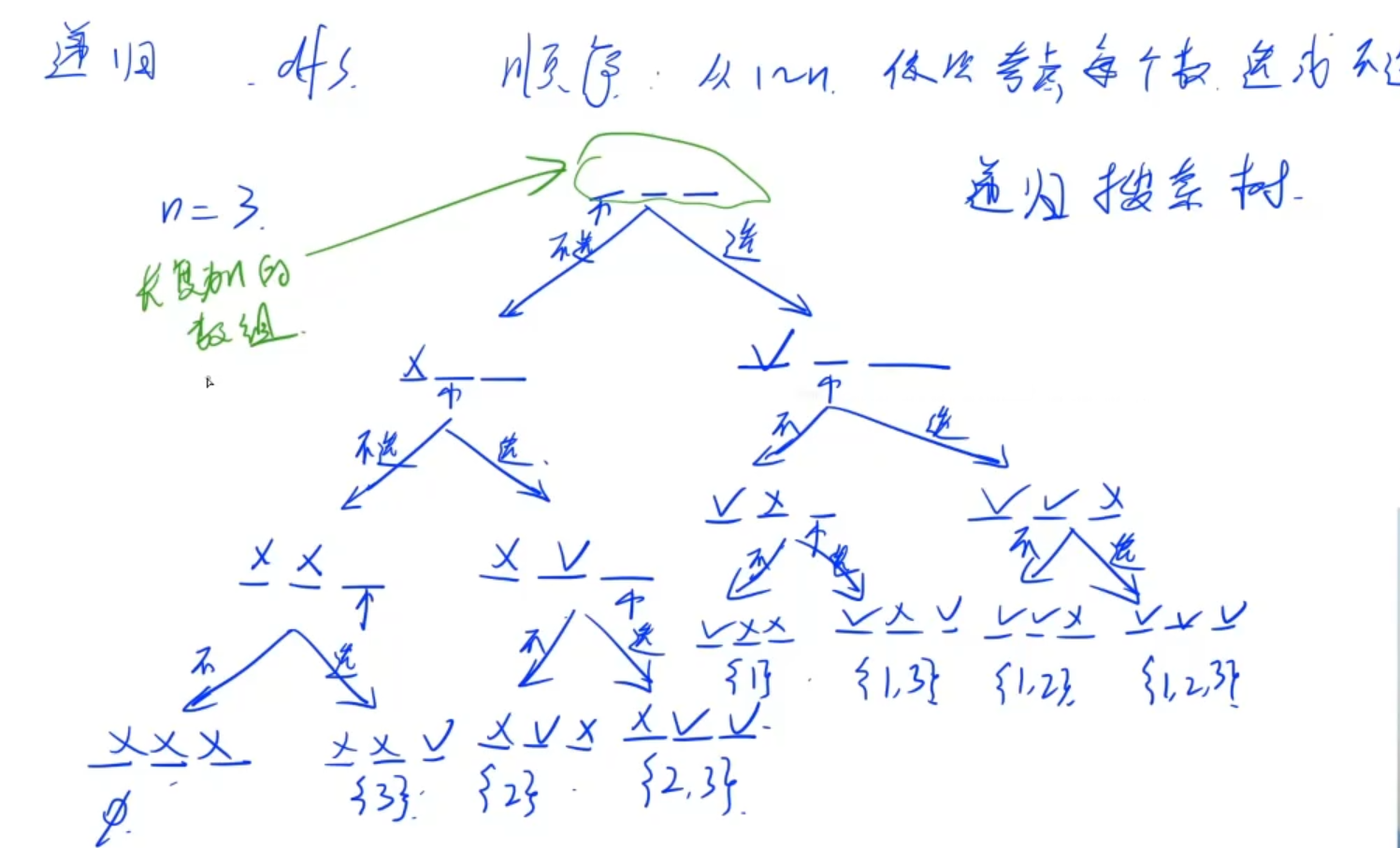
递归实现指数型枚举

从1-n选任意多个数，输出所有方案。

代码

#include<cstdio>
#include<string> 
#include<iostream>
#include<algorithm>

using namespace std;

//从1-n选任意多个数，输出所有方案。
//顺序原则，从1-n顺序考虑每个数选或不选。 
const int N = 15;
int n;
int st[N]; //状态：记录每个位置当前的状态，0表示未考虑，1表示选，2表示不选。 
int way[1 << 15][16],cnt; 

void dfs(int u)
{
	if (u > n)
	{
		for (int i = 1; i <= n; i ++ )
			if (st[i] == 1)
			   printf("%d ",i);
   		puts("");
//		for (int i = 1; i <= n; i ++ )
//			if (st[i] == 1)
//			   way[cnt][i] = i;
//        cnt++;//不重要只是记录进入if的次数 
		return ;   
	}
	
	st[u] = 1;
	dfs(u + 1);// 选 
	st[u] = 0;// 恢复现场 
	
	st[u] = 2;
	dfs(u + 1);// 不选 
	st[u] = 0;// 恢复现场 
}

int main()
{
	scanf("%d",&n);
	
	dfs(1);
//	for (int i = 0; i < cnt; i ++ )
//	{
//		for (int j = 1; j <= n; j ++ )
//		printf("%d",way[i][j]);
//		puts("");
//	}
	return 0;
}

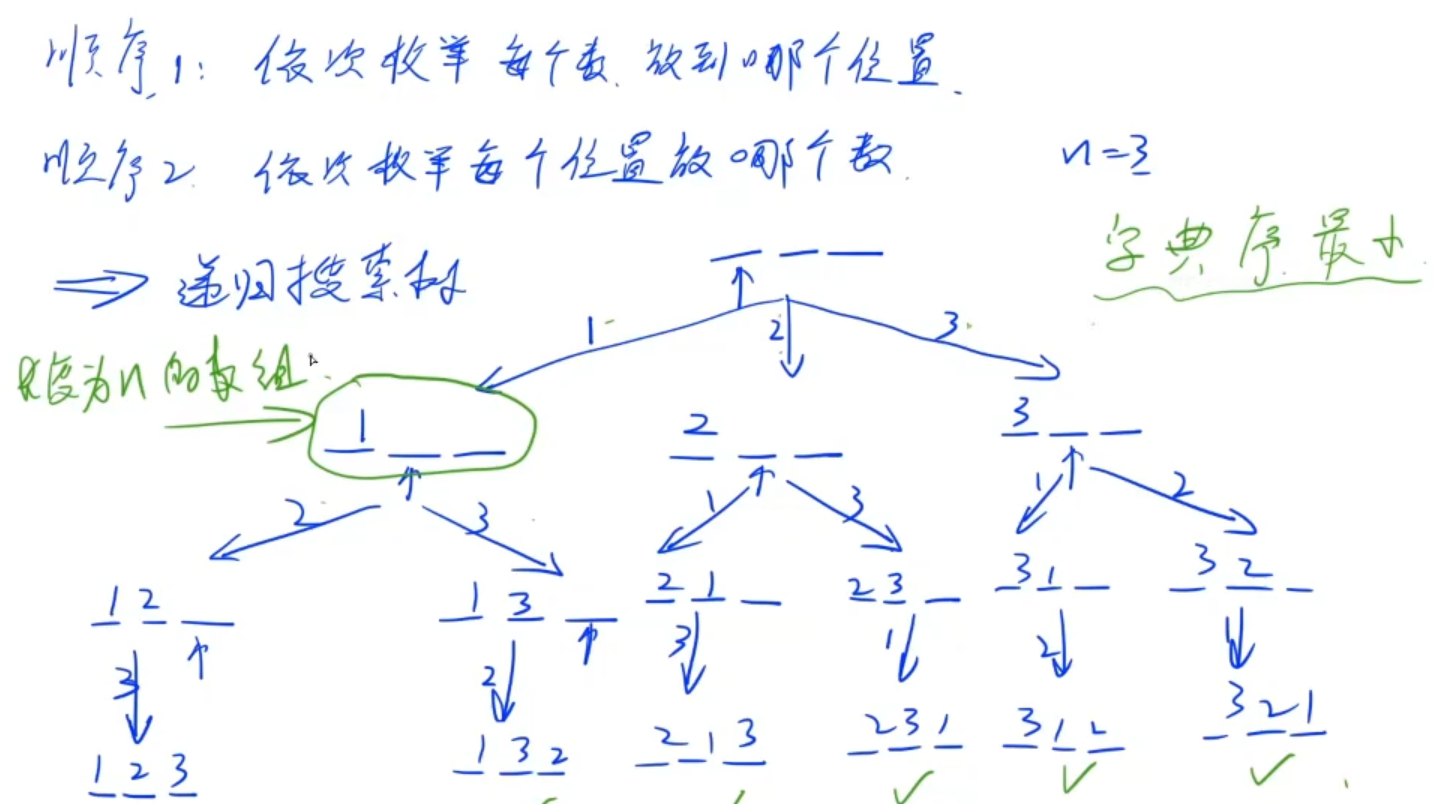
递归实现排列型枚举

给一个数n，按字典序输出所有全排列。（n<10）

代码

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 10;
int n;
int st[N];
bool used[N];//true表示用过，false表示没用
 
//时间复杂度O(n*n!)
 
void dfs(int u)
{
	if (u > n)//边界 
	{
		for (int i = 1; i <= n; i ++ )
		 	printf("%d ",st[i]);
		puts("");
		return;
	}
	//依次枚举每个分支，即当前位置可以填那些数 
	for (int j = 1; j <= n; j ++ ) 
		{
			if (!used[j])
			{
		 	   st[u] = j;
			   used[j] = true;
			   dfs(u + 1);
			   //恢复现场 
			   st[u] = 0;//可省略  
			   used[j] = false;
			}
		}
		
}

int main()
{
	scanf("%d",&n);
	dfs(1);
	return 0;
}

递推

先求解子问题再推出原问题。
求解斐波那契数列的前n项。

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;
int n;

//空间压缩
 
int main()
{
	cin>>n;
	int a = 0,b = 1;
	for (int i = 1; i <= n; i ++ )
	{
		cout<<a<<' ';
		int fn = a + b;
		a = b;
		b = fn;
	}
	return 0;
}
//普通做法 

//int main(){
//	scanf("%d",&n);
//	int f[46];
//	f[1] = 0;
//	f[2] = 1;
//	for (int i = 3; i <= n; i ++ )
//		f[i] = f[i-1] + f[i-2];
//	for (int i = 1; i <= n; i ++ )
//		cout<<f[i]<<" ";
//	cout<<endl;
//    return 0;
//}

费解的开关

这句位运算代码if ((op >> i) & 1)是什么意思？
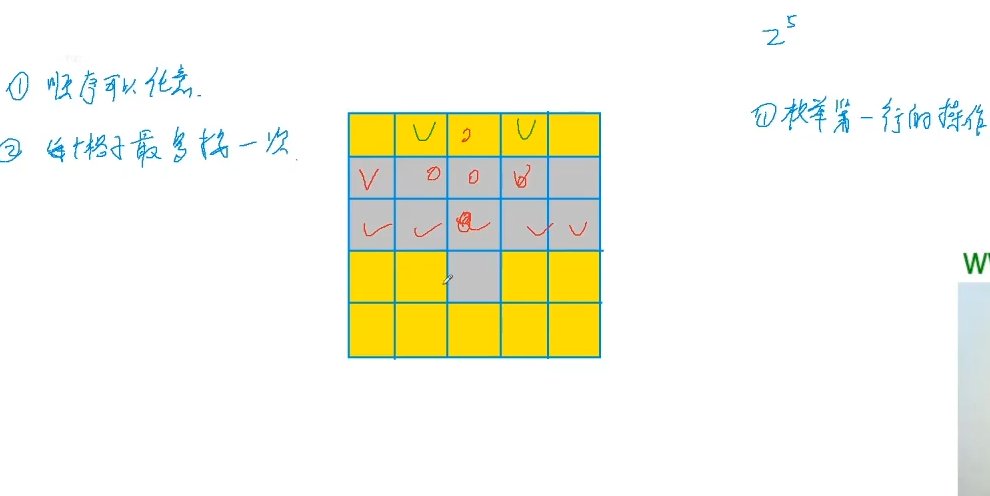
第一行有32种按下开关的方式，与输入数据的方案无关。
第一行用的二进制枚举按下开关的方式，我们用一个5位的二进制数来表示一种按下开关的方式，如果第i个灯需要按一下，那么对应的二进制数的第i位就是1，否则就是0。（当然你也可以如果是0就按，否则是1不按。例如：0的五位二进制00000和31的五位二进制11111，不管选0 or 1，都要按下5次。）
5位的二进制数一共有32个，分别是0_{31，所以我们循环0}31，就可以遍历所有操作方式了。

这道题递归思想体现在哪？
每一行开关的操作完全被上一行灯的亮灭所决定。

如何构造turn函数，g[a][b] ^= 1是什么意思？
首先构造五个变化位置x，y的坐标。在0变1，1变0时，使用位运算的异或操作。
异或：如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

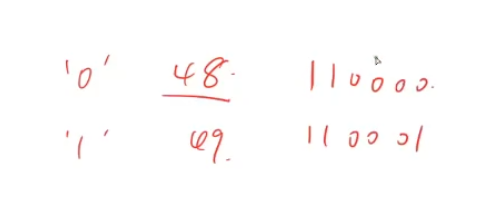
我们还可以发现下面两个性质：

按2次相当与没有按。

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 6;

char g[N][N],backup[N][N];
int dx[5] = {-1,0,1,0,0},dy[5] = {0,1,0,-1,0};
void turn(int x,int y)
{
	for (int i = 0; i < 5; i ++ )
	{
	 	int a = x + dx[i],b = y + dy[i];
		if (a < 0 || a >= 5 || b < 0 || b >= 5)continue;
		//0变1，1变0 
  		g[a][b] ^= 1;   
	}

}

int main(){
	int T;
	scanf("%d",&T);
	while(T--)
	{
		//一次读入一行五个数 
		for (int i = 0; i < 5; i ++ )cin>>g[i];
		
		int res = 10;
		//第一行有32种按下开关的方式，与输入数据无关。
		for (int op = 0; op < 32; op ++ )
		{
			//备份g数组 
			memcpy(backup,g,sizeof g);
			// 操作步数 
			int step = 0;
		
			//对于首把op的二进制形式的0-4位都与上一 
			for (int i = 0; i < 5; i ++ )
				if ((op >> i) & 1)
				{
					step++;
					turn(0,i);
				}
			for (int i = 0; i < 4; i ++ )//枚举前四行 
				for (int  j = 0; j < 5; j ++ )//一行有5位 
					if (g[i][j] == '0')//如果i行j位为0 
					{
						step++;
						turn(i + 1,j);//i+1行按下开关 
					}
					
			//判断最后一行是否全亮 
			bool dark = false;
			for (int i = 0; i < 5; i ++ )
				if (g[4][i] == '0')
				{
					dark = true;
					break;
				}
			//如果全亮更新步数 
			if (!dark) res = min(res,step);
			//恢复备份 
			memcpy(g,backup,sizeof g);	
		}
		if (res > 6) res = -1;
		cout<<res<<endl;
	}
    return 0;
}

习题