P3383 【模板】线性筛素数

埃氏筛法

埃氏筛法的基本思想 ：从2开始，将每个质数的倍数都标记成合数，以达到筛选素数的目的。
代码 ：

int visit[maxn]; 
void Prime(){
    mem(visit,0);           //初始化都是素数
    visit[0] = visit[1] = 1;  //0 和 1不是素数
    for (int i = 2; i <= maxn; i++) {
        if (!visit[i]) {         //如果i是素数，让i的所有倍数都不是素数
            for (int j = i*i; j <= maxn; j += i) {
                visit[j] = 1;
            }
        }
    }

}

这里有一个小优化，j 从 i * i 而不是从 i + i开始，因为 i*(2~ i-1)在 2~i-1时都已经被筛去，所以从i * i开始。

埃氏筛法的缺陷 ：对于一个合数，有可能被筛多次。例如 30 = 2 * 15 = 3 * 10 = 5*6……那么如何确保每个合数只被筛选一次呢？

 

欧拉筛法

欧拉筛法的基本思想 ：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。
代码 ：

int prime[maxn];
int visit[maxn];
void Prime(){
    mem(visit,0);
    mem(prime, 0);
    for (int i = 2;i <= maxn; i++) {
        cout<<" i = "<<i<<endl;
        if (!visit[i]) {
            prime[++prime[0]] = i;      //纪录素数， 这个prime[0] 相当于 cnt，用来计数
        }
        for (int j = 1; j <=prime[0] && i*prime[j] <= maxn; j++) {
//            cout<<"  j = "<<j<<" prime["<<j<<"]"<<" = "<<prime[j]<<" i*prime[j] = "<<i*prime[j]<<endl;
            visit[i*prime[j]] = 1;
            if (i % prime[j] == 0) {
                break;
            }
        }
    }

1.对于visit[i*prime[j]] = 1 的解释： 这里不是用i的倍数来消去合数，而是把 prime里面纪录的素数，升序来当做要消去合数的最小素因子。

打表观察来理解 ：

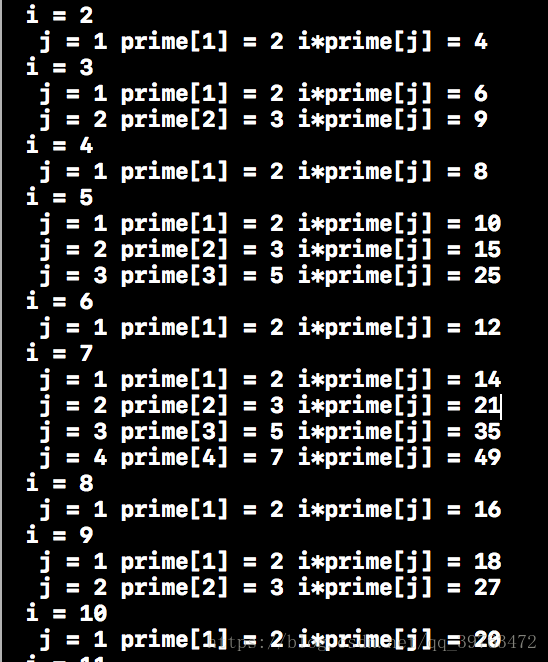
发现i在消去合数中的作用是当做倍数的。

2.对于 i%prime[j] == 0 就break的解释 ：当 i是prime[j]的倍数时，i = kprime[j]，如果继续运算 j+1，i * prime[j+1] = prime[j] * k prime[j+1]，这里prime[j]是最小的素因子，当i = k * prime[j+1]时会重复，所以才跳出循环。
举个例子 ：i = 8 ，j = 1，prime[j] = 2，如果不跳出循环，prime[j+1] = 3，8 * 3 = 2 * 4 * 3 = 2 * 12，在i = 12时会计算。因为欧拉筛法的原理便是通过最小素因子来消除。

————————————————
版权声明：本文为CSDN博主「彤云望月」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_39763472/article/details/82428602