OO第一单元作业总结

OO第一单元作业总结

第一次作业

第一次作业多项式只包括幂函数和常数，没有括号等复杂组合，也没有要求对输入进行格式检查，并且在做第一次作业时，没有考虑过之后的扩展问题，也不知道递归下降分析，在设计程序时仍然保留了大量面向过程的思想，虽然第一次作业顺利完成，第二次作业却无法避免的重构了。

第一次作业的实现思路

（1）建立预处理类，对输入字符串进行预处理，将空字符清除；将多正负号化为一个；用字母来代替正负号，以防止通过加减号分割字符串时将正负号误判。

（2）建立单项式类和获取单项式类，获取单项式类将经过预处理的字符串通过加减号分割成若干个单项式，将每个单项式的常数和指数计算出来，生成一个单项式类，保存在hashmap中。

（3）hashmap添加单项式时将相同指数的单项式进行合并，对于每个单项式类，重写tostring返回该单项式的导数，最后遍历hashmap输出。

程序结构分析

度量

指标名	平均值	总值
本质复杂度	3.00	21
设计复杂度	4.57	32
循环复杂度	4.71	33
平均操作复杂度	4.14
加权方法复杂度	7.25	29

由于第一次作业的题目比较简单，可以看出代码的复杂度并不高，通过hashmap的合并功能对输出进行优化也没有影响整体的性能。

UML类图

由于第一次作业较为简单，类之间耦合度较低，类的构造也比较简单。

BUG

本次实验在互测中共发现两处bug，分别是没有考虑有三个连续正负号和没有用BigInteger存放指数，在互测时并没有发现别人的错误。

第二次作业

第二次作业添加了三角函数和括号，难度远高于第一次，括号和三角函数的加入使得第一次作业的实现思路无法继续用于第二次，只好进行重构。

第二次作业实现思路

由于第二次作业没有要求检查格式，因此本次作业的重点放在了求导上。通过大一下数据结构的学习，在进行表达式计算时可以使用后缀表达式的方法通过栈操作计算，将对表达式的求导看成对表达式的计算，本次作业选择了表达式树的方法实现表达式求导。

（1）将三角函数，幂函数，常数看作运算数，加号，减号和乘号看作运算符，通过将中缀表达式转化为后缀表达式，获得包含了三角函数，幂函数，常数，加号，减号和乘号的元素栈。

（2）构造常数类，幂函数类，三角函数类和多项式类，能获得对应因子的原函数和导函数，再构造加法运算类，减法运算类和乘法运算类来对两个元素进行求导计算，每次运算产生新的多项式类，运算结束后最后一个多项式类的导函数就是原表达式的导函数。

程序结构分析

度量

指标名	平均值	总值
本质复杂度	3.43	120
设计复杂度	3.63	127
循环复杂度	4.00	140
平均操作复杂度	3.69
加权方法复杂度	9.21	129

第二次作业相较于第一次作业的复杂度变化并不大，但通过表达式树求导无法对可以合并的因子进行合并，更不能对三角函数进行化简，因此第二次作业在性能方面的分数很低，如果在多项式类中添加hashmap去合并因子会对输出进行显著优化，但复杂度会大大增加。此外，第二次作业大量使用栈的操作，相较于递归消耗更多时间，但节省了内存。

UML类图

BUG

本次作业虽然通过了中测，但强测只过了三个点，结果发现在中序表达式转后序表达式时出现了错误，改正后又出现了输出格式错误，经过检查发现在求导时为了优化表达式，导函数的输出出现了不合法的形式。

第三次作业

为了保留第二次作业的求导功能，第三次作业选择了判断表达式合法性和表达式求导分离的 方法，新建了判断表达式合法性的判断类，使用类似递归下降分析的方法使用递归函数判断表达式的合法性，符合规范的表达式再进行求导。与第二次求导不同的是，第三次作业中对三角函数的求导进行了重构，三角函数内部当作新的表达式递归求导，输出方式与第二次相同。

第三次作业实现思路

第三次作业与第二次主要的区别在判断表达式的合法性，为此构建了Judge类，判断合法性的具体方法如下：

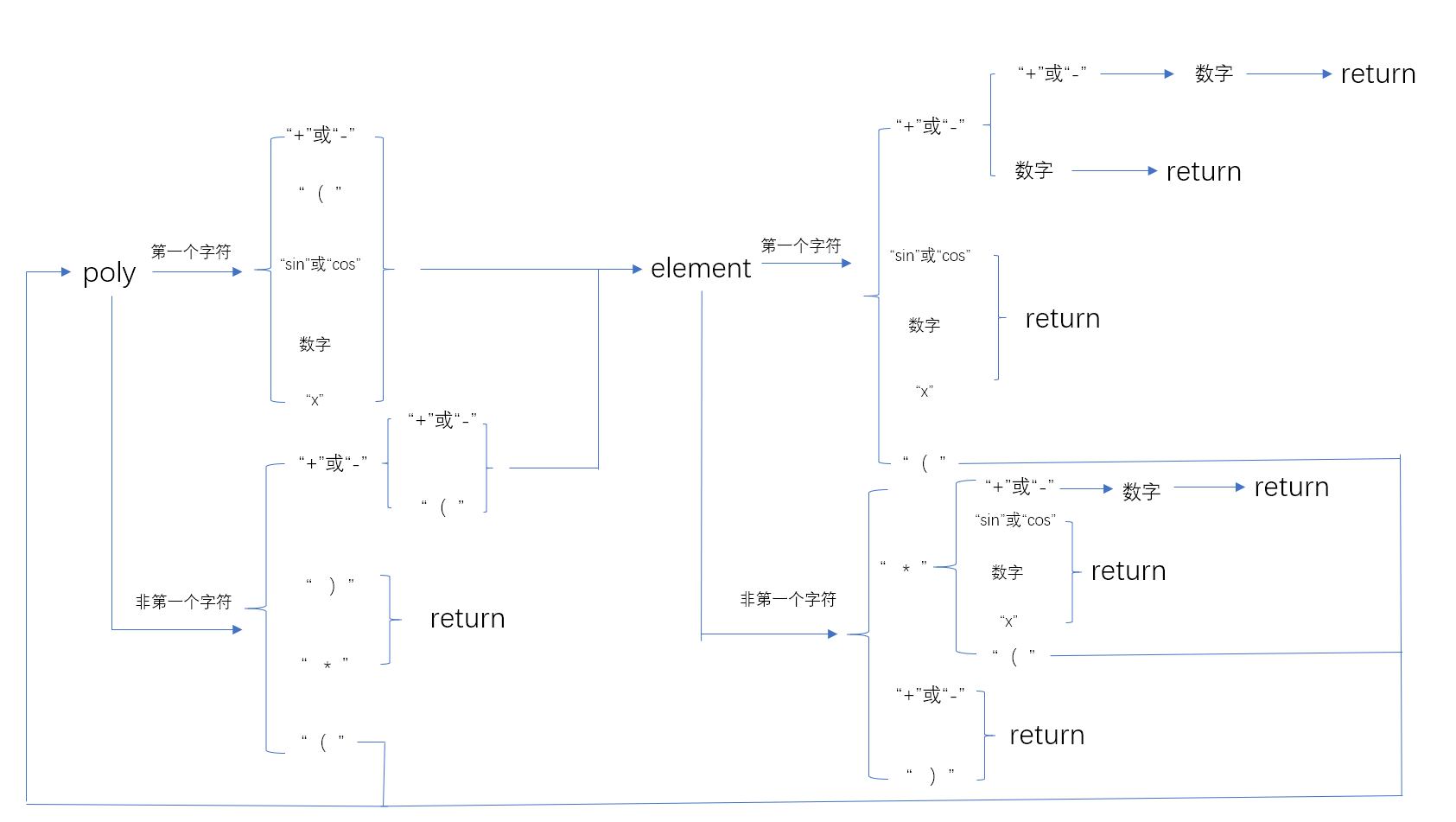
对于指数和括号匹配的判断，则放在表达式判断之外额外进行判断。

关于三角函数的求导，将三角函数内部的表达式求导得到的导函数和原函数，即可根据求导原则得到三角函数的导函数和原函数。

程序结构分析

度量

指标名	平均值	总值
本质复杂度	3.19	172
设计复杂度	3.87	209
循环复杂度	4.91	265
平均操作复杂度	4.33
加权方法复杂度	15.60	234

可以看出，新增的Judge类使程序的复杂度剧增，主要原因是Judge类通过对字符逐一读取判断，使用的是面向过程的思想，如果面向对象的方法，通过递归下降分析，可以降低表达式分析时的复杂度，大幅提高程序性能。

UML类图

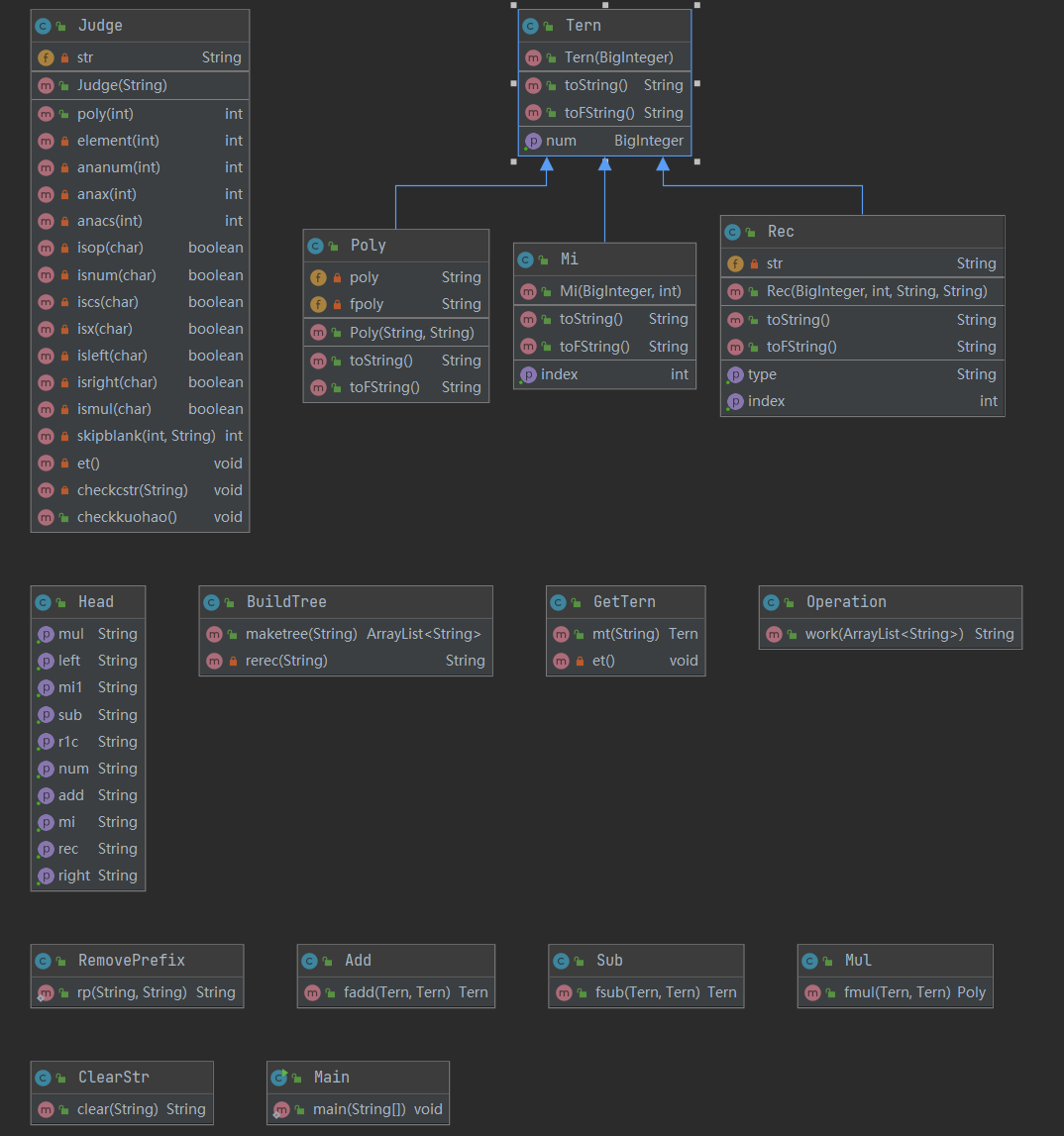
BUG

本次作业的BUG出现在表达式合法性的判断上，在三角函数内部因子合法性的判断时，忘记了考虑空白字符，在element函数中忽略了一种输入“+”或“-”的情况，还修复了第二次作业遗留的导函数格式错误。

总结

第一单元作业对我来说难度极大，为了保证能提交作业，有时只好用面向过程的思想来解决问题，也没有足够的时间去思考最优的架构，更没有时间去优化输出。现在反思第一单元的作业，可以优化的地方有很多，用面向过程的地方也可以用面向对象来替代，代码的风格也可以进一步优化。课上讲的内容虽然对完成作业没有直接的帮助，但是理论课对面向对象的讲解让我对面向对象的认识更加清晰，知道了使用面向对象思想让代码更加规范合理。虽然第一单元已经结束，但我深刻体会到自己能力的欠缺，还需要掌握更多知识，为下一个任务做准备。