[算法]初探FHQ_treap算法与应用
写在前面
fhq-treap是最近几天学平衡树的时候恰巧遇到的，学习后深感fhq思想的厉害，于是便忍不住写了这篇文章。
我的实力水平不够，所以若是内容有差错或有疏漏的，请指出谢谢。
前置知识：二叉搜索树->平衡树（最好把treap学了）
算法简析
首先根据名字我们就知道了，fhq-treap相当于treap强化版。
Q：对于这个数据结构有什么用？
A：它可以完成单点修改，区间修改，单点查询，区间查询等，也就是说可以代替treap与splay（这里有些不严谨，但我就是用fhq treap代替splay用的）
我们都知道平衡树其实区别就在于它的核心操作平衡部分，对于fhq treap，它有两个核心部分：
1.split 英文是分裂的意思，它的作用就是将一颗树分成两颗树
2.Merge 合并，它的作用是将两棵树合并成一颗树
可能初看这两个操作，你完全想不到怎么用于平衡树，下面是分析。
关于下面的结构体内变量解释：
1.lson：左子树的地址
2.rson：右子树的地址
3.size：以当前位置的根的树的大小
4.fix：修正值，这是一个随机数，用于维护平衡
5.val：权值
函数名解释
1.Insert 插入
2.Delete 删除
3.update_size 更新当前位置为根的树的大小
1.split
常见分裂的方法一般有两种，一种是按照排名分裂，另一种是按照权值分裂。
本质上其实都是一致的，比方说对于一个序列
我们需要将它在树中分成1~3与4~6两颗树
那么它在树中便是这样切开
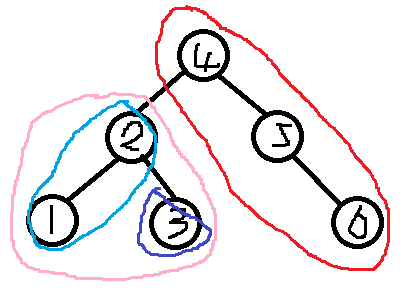
其中红色与粉色便是最终分裂出来的两棵树
可能这有些难理解所以还是结合代码自己好好想想
//这里是以排名为基准分裂的
inline void split(int r,int k,int &x,int &y) { if(!r) x = y = 0;//因为啥都没有所以无法分裂 else{ if(k <= fhq[fhq[r].lson].size) y = r,split(fhq[r].lson,k,x,fhq[r].lson); else x = r,split(fhq[r].rson,k - fhq[fhq[r].lson].size - 1,fhq[r].rson,y); update_size(r); } return ; }
2.Merge
那么对于两颗分裂的树，在分裂后肯定要将它们合并为新的树
维护平衡的操作也在这里
在treap中我们通过比较 fix 修正值来进行左旋右旋维护平衡
在fhq-treap中合并操作也是通过fix值维护平衡
首先我们知道分裂后得到的两棵树是左子树与右子树
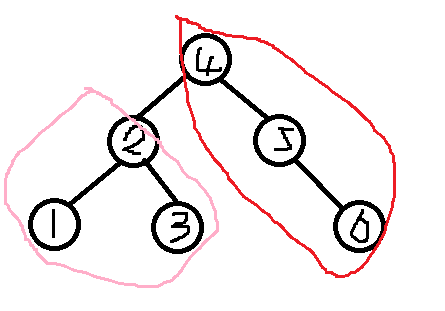
重点：根据二叉搜索树的性质，左子树任何节点都小于右子树任何节点
也就是说，左子树的右子树（即图中以3为根的树）与右子树（即图中以4为根的树）也满足左子树与右子树性质（这句话很乱结合图多看看）
所以我们就可以合并这两颗树，即合并以3为根的树与以4为根的树，最后以这颗新的合并的树成为2为根的右子树（乱，多看图理解）
这就是合并的原理，另一种情况同理
inline int Merge(int x,int y) { if(!x || !y) return x|y;//返回那个有子树的坐标 else{ if(fhq[x].fix > fhq[y].fix){ fhq[x].rson = Merge(fhq[x].rson,y); update_size(x); return x; } else{ fhq[y].lson = Merge(x,fhq[y].lson); update_size(y); return y; } } }
于是乎，我们就知道这两个操作是如何实现的了
但是可能还不知道如何应用与修改等操作中
应用
我们可以用一个序列帮助理解
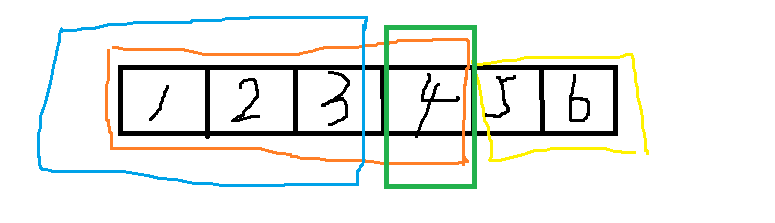
因为我懒得写代码，所以这里只提供思路，请另寻大佬们的代码
假设我们想要删掉值为 4 的节点
我们可以先通过 Split 操作将树分为1~4(橙) 与 5~6（黄）两个子树
再通过一次 Split 操作将（橙）树分为1~3（蓝） 与 4（绿） 两个子树
然后将蓝黄树合并就可以了
如果你看懂了，你就会明白fhq treap的魅力在哪里。
同理，对于区间删除，我们只需要改变分裂大小也可以分成三颗树，然后合并其中你留下的两颗就行了
而对于单点区间修改，在分裂为三颗树后，我们对于我们需要的树，根节点打下一个标记（加法，减法，乘法等等），在后来的分裂合并操作中，下传标记就好了。
练习
对于fhq treap的题，其实大部分的平衡树题都能用，这里就只放出三个
难度依次递进
发牢骚写在后面
已经是准高一了，明明退役还只有半年但还是又继续学oi了，希望自己能进步吧。
