强化学习-马尔可夫决策过程

参考：

（1）强化学习（第二版）

（2）https://b23.tv/fOmHymj（推荐）

（3）https://www.cnblogs.com/pinard/p/9426283.html

（4）https://blog.csdn.net/liweibin1994/article/details/79079884

（5）https://deepmind.com/learning-resources/-introduction-reinforcement-learning-david-silver

一、智能体与环境的交互以及马尔可夫性

1、智能体与环境的交互过程可以表示为一个序列：

（1）对于某些任务来说，智能体和环境的交互过程是有“终止时刻”的，此时，我们把智能体与环境的每一个交互序列称为一幕(episode)，这样的任务就称为“分幕式任务”。交互序列表示为：$S_{0}，A_{0}，R_{1}，S_{1}，A_{1}，R_{2}，S_{2}，......，S_{T-1}，R_{T-1}，S_{T}$。

（2）对于某些任务来说，智能体和环境的交互过程是在不断发生的，这样的任务就称为“持续性任务”。交互序列表示为：$S_{0}，A_{0}，R_{1}，S_{1}，A_{1}，R_{2}，S_{2}，......$

2、马尔可夫性：$S_{t+1}$和$R_{t+1}$的产生只取决于前一个状态$S_{t}$和前一个动作$A_{t}$，而与更之前的状态和动作无关。

二、关键概念

1、状态集合：$\mathcal{S}$，$S_{t}$表示t时刻的状态。

2、动作集合：$\mathcal{A}$，$A_{t}$表示t时刻的动作。

3、收益集合：$\mathcal{R}$，$R_{t}$表示t时刻的收益。

4、状态转移概率：$p\left( s',r|s,a \right)=Pr\left( S_{t+1}=s',R_{t+1}=r|S_t=s,A_t=a \right)$。$\sum_{s'\in \mathcal{S}}{\sum_{r\in \mathcal{R}}{p\left( s',r|s,a \right)}}=1, \forall s\in \mathcal{S}, \forall a\in \mathcal{A\left( s \right)}$。

5、回报：$G_t$。对于分幕式任务来说，回报可以表示为收益的总和，即$G_t=R_{t+1}+R_{t+2}+......+R_{T}$。但是对于持续性任务，这种表示方式会导致其趋向于无穷，因此，我们引入一个额外的概念，即折扣。$G_t=R_{t+1}+\gamma R_{t+2}+\gamma ^2R_{t+3}+......=\sum_{k=0}^{\infty}{\gamma ^kR_{t+k+1}}$。其中$\gamma$表示折扣率，$\gamma \in [0,1]$（持续性任务$\gamma<1$）。当$\gamma=0$时，智能体只关心当前收益，而当$\gamma$趋近于1时，智能体将更多地考虑未来的收益。

6、策略：$\pi$，$\pi\left(a|s\right)=Pr\left(A_t=a|S_t=s\right)$，针对某个状态既可以采取确定性的策略也可以采取随机策略。

7、状态价值函数：$v_\pi \left(s\right)=E_\pi \left[G_t|S_t=s\right]$。

8、动作价值函数：$q_\pi \left(s,a\right)=E_\pi \left[G_t|S_t=s,A_t=a\right]$。

9、回溯图：

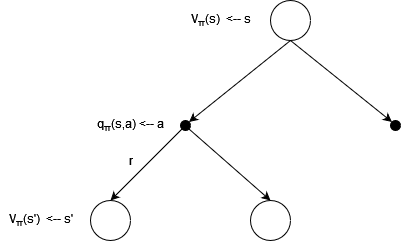
以下提到的公式都可以根据回溯图得到比较好的理解。

10、贝尔曼方程：

$
\begin{aligned}
    v_{\pi}\left( s \right) &=E_{\pi}\left[ G_t|S_t=s \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma R_{t+2}+\gamma ^2R_{t+3}+...|S_t=s \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma \left( R_{t+2}+\gamma R_{t+3}+... \right)|S_t=s \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma G_{t+1} |S_t=s \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma v_{\pi}\left( S_{t+1} \right) |S_t=s \right]\\
    &=\sum_{a}{\pi\left( a|s \right)\sum_{s',r}{p\left( s',r|s,a \right)\left[ r+\gamma v_{\pi}\left( s' \right) \right]}}
\end{aligned}
$

$
\begin{aligned}
    q_{\pi}\left( s,a \right) &=E_{\pi}\left[ G_{t}|S_{t}=s,A_{t}=a \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma R_{t+2}+\gamma ^2R_{t+3}+...|S_{t}=s,A_{t}=a \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma \left( R_{t+2}+\gamma R_{t+3}+... \right)|S_{t}=s,A_{t}=a \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma G_{t+1} |S_{t}=s,A_{t}=a \right]\\
    &=E_{\pi}\left[ R_{t+1}+\gamma q_{\pi}\left( S_{t+1},A_{t+1} \right) |S_{t}=s,A_{t}=a \right]\\
    &=\sum_{s',r}{p\left( s',r|s,a \right)\left[ r+\gamma \sum_{a'}{\pi\left(a'|s'\right)q_{\pi}\left( s',a' \right)} \right]}
\end{aligned}
$

（1）$v_{\pi}\left( s \right)=\sum_{a}{\pi\left( a|s \right)\sum_{s',r}{p\left( s',r|s,a \right)\left[ r+\gamma v_{\pi}\left( s' \right) \right]}}$

（2）$q_{\pi}\left( s,a \right)=\sum_{s',r}{p\left( s',r|s,a \right)\left[ r+\gamma \sum_{a'}{\pi\left(a'|s'\right)q_{\pi}\left( s',a' \right)} \right]}$

还有两个比较重要的公式：

（3）$v_{\pi}\left( s \right) =\sum_a{\pi \left( a|s \right) q_{\pi}\left( s,a \right)}$

（4）$q_{\pi}\left( s,a \right) =\sum_{s',r}{p}\left( s',r|s,a \right) \left( r+\gamma v_{\pi}\left( s' \right) \right) $

11、最优策略

对于最优策略${\pi}_*$和其他任何策略${\pi}$来说，都有$v_{\pi_*}\left( s \right)\geqslant v_{\pi}\left( s \right)$，$\forall s\in \mathcal{S}$。最优策略对应最优价值函数。

12、最优价值函数

$v_*\left( s \right)=\underset{\pi}{max}v_{\pi}\left( s \right)$，$\forall s\in \mathcal{S}$

$q_*\left( s,a \right)=\underset{\pi}{max}q_{\pi}\left( s,a \right)$，$\forall s\in \mathcal{S}$，$\forall a\in \mathcal{A}$

13、贝尔曼最优方程

（1）$v_*\left( s \right)=\underset{a}{max}\left( \sum_{s',r}{p(s',r|s,a)(r+\gamma v_*(s'))} \right)$

（2）$q_*\left( s,a \right)=\sum_{s',r}{p\left( s',r|s,a \right)\left( r+\gamma \underset{a'}{max}q_*(s',a') \right)}$

还有两个比较重要的公式：

（3）$v_*\left( s \right)=\underset{a}{max}q_*\left( s,a \right)$

（4）$q_*\left( s,a \right)=\sum_{s',r}{p\left( s',r|s,a \right)\left( r+\gamma v_*(s') \right)}$