E - Reachability in Functional Graph

E - Reachability in Functional Graph

https://atcoder.jp/contests/abc357/tasks/abc357_e

 

思路

概念：

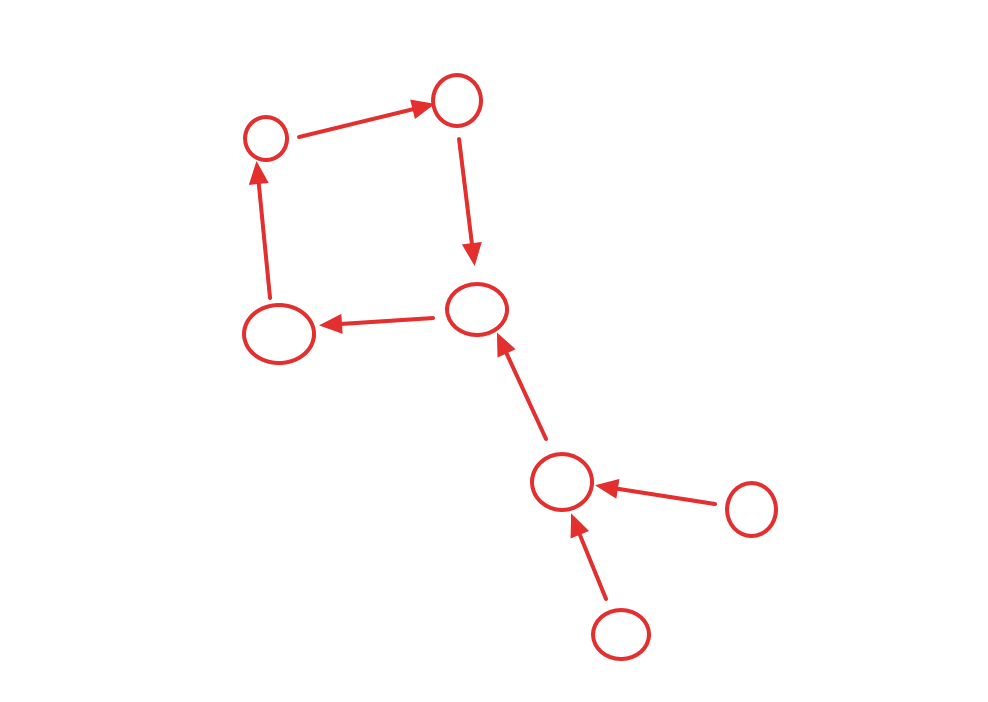
基环树-内生树。

https://www.cnblogs.com/Dfkuaid-210/p/14696378.html

方法：

使用拓扑排序，从入度为0的点开始，依此从外层向内层拆点，直到剩下环， 拆换过程中把拆掉的tocnt记到目标点上tocnt，依次累计到环点上。

环点上的所有点的tocnt == 环上点所有tocnt之和。

最后统计所有点的tocnt。

 

 

 

 

 

Code

https://atcoder.jp/contests/abc357/submissions/54538162

LL n;
/*
to[i]  -- i means vertex index, to[i] means its next vertex from vertex i.
todeg[i] -- i means vertex index, todeg[i] means how many vertice are to this vertex from other vertice.
tocnt[i] -- i means vertex index, tocnt[i] means how many vertice can reach to this vertex.
*/
LL to[200005], todeg[200005], tocnt[200005];
vector<LL> circle;

LL dfs(LL i){
    if (todeg[i] == 0) return 0;
    
    circle.push_back(i);
    
    todeg[i] = 0;
    
    LL current = tocnt[i];
    LL others = dfs(to[i]);
    
    LL sum = current + others;
    
    return sum;
}

int main()
{
    cin >> n;

    /*
    input and initialize todeg and tocnt
    */
    for(int i=1; i<=n; i++){
        cin >> to[i];
        
        todeg[to[i]]++;
        
        /*
        every vertex has one vertex to it at least, which is itself.
        so tocnt == 1
        */
        tocnt[i] = 1;
    }

    /*
    do toposort to remove all non-circle vertice,
    then at last there are some circle left.
    */
    queue<LL> qq;
    for(int i=1; i<=n; i++){
        if (todeg[i]==0){
            qq.push(i);
        }
    }

    while(!qq.empty()){
        LL front = qq.front();
        qq.pop();
        
        tocnt[to[front]] += tocnt[front];
        
        todeg[to[front]]--;
        if (todeg[to[front]] == 0){
            qq.push(to[front]);
        }
    }

    /*
    for all circle vertice, its tocnt actually contains two parts:
    (1) tocnt[i] -- from non-circle vertice which can reach i
    (2) tocnt[j] -- j<>i, other circle vertice in this circle
    that mean for each circle vertex,
    tocnt[i] == sum(tocnt[j]|j belong to this circle)
    */
    for(int i=1; i<=n; i++){
        if (todeg[i]){
            circle.clear();
            LL circle_sum = dfs(i);
            
            for(auto one: circle){
                tocnt[one] = circle_sum;
            }
        }
    }

    /*
    count all vertice's tocnt
    */
    LL ans = 0;
    for(int i=1; i<=n; i++){
        ans += tocnt[i];
    }

    cout << ans << endl;
    
    return 0;
}