dynamic programming

Definition

https://en.wikipedia.org/wiki/Dynamic_programming

数学和计算机程序上的术语。

如果一个复杂的问题能够分解成更加简单的子问题，并且有最佳子结构， 那么此问题可应用动态规划。

负责问题的最优解，可以从子问题的最优解找到。

 

类似数学上目标函数为凸函数的情况。

总体上的最优解，也是局部上的最优解。

 

Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.

In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have optimal substructure.

If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.^[1] In the optimization literature this relationship is called the Bellman equation.

 

复杂问题分解为子问题， 如果没有最优结构，即使使用了递归解法，也不能成为动态规划。

例如 归并排序 和 快速排序。

There are two key attributes that a problem must have in order for dynamic programming to be applicable: optimal substructure and overlapping sub-problems. If a problem can be solved by combining optimal solutions to non-overlapping sub-problems, the strategy is called "divide and conquer" instead.^[1] This is why merge sort and quick sort are not classified as dynamic programming problems.

 

------------恢复内容开始------------

Definition

https://en.wikipedia.org/wiki/Dynamic_programming

数学和计算机程序上的术语。

如果一个复杂的问题能够分解成更加简单的子问题，并且有最佳子结构， 那么此问题可应用动态规划。

负责问题的最优解，可以从子问题的最优解找到。

 

类似数学上目标函数为凸函数的情况。

总体上的最优解，也是局部上的最优解。

 

Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.

In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have optimal substructure.

If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.^[1] In the optimization literature this relationship is called the Bellman equation.

 

复杂问题分解为子问题， 如果没有最优结构，即使使用了递归解法，也不能称为动态规划。

例如 归并排序 和 快速排序。

There are two key attributes that a problem must have in order for dynamic programming to be applicable: optimal substructure and overlapping sub-problems. If a problem can be solved by combining optimal solutions to non-overlapping sub-problems, the strategy is called "divide and conquer" instead.^[1] This is why merge sort and quick sort are not classified as dynamic programming problems.

 

Characteristics of dynamic programming

https://www.indeed.com/career-advice/career-development/dynamic-programming

相同的子问题非单一出现， 会出现多次。

子结构具有最优化性质， 子问题的最优解，可以推导出更高一层的子问题的最优解。

 

Dynamic programming has two important characteristics, which include:

1. Subproblems overlap

Subproblems are smaller variations of an original, larger problem. For example, in the Fibonacci sequence, each number in the series is the sum of its two preceding numbers (0, 1, 1, 2, 3, 5, 8,...). If you want to calculate the nth Fibonacci value in the sequence, you can break down the entire problem into smaller subproblems. These subproblems then overlap with one another as you find solutions by solving the same subproblem repeatedly.

The overlap in subproblems occurs with any problem, which allows you to apply dynamic programming to break down complex programming tasks into smaller parts.

Related: FAQ: What Is an Iteration in Computer Science? (With Examples)

2. Substructure has optimal property

Optimal substructure property materializes when you can arrive at an optimal solution after constructing all the other solutions that occurred from every subproblem you solved. The solution you calculate from each overlap applies to the overall problem in order to function and optimize recursion. In the example of the Fibonacci sequence, each subproblem contains a solution that you can apply to each successive subproblem to find the next number in the series, making the entire problem display optimal substructure property.

 

Dynamic programming methods

https://www.indeed.com/career-advice/career-development/dynamic-programming

解法有两种：

（1）从上而下方法， 编写函数，原始问题拆分成子问题后，子问题的解法为递归调用次函数。-- 结合计算结果记忆方法。

（2）从下而上方法，从最小的问题开始计算出最优解， 然后组合最小问题的最优解，获得更高一级问题的最优解， 直到原始问题。 -- 结合表格方法存储计算结果。

When applying dynamic programming to your projects, you can implement two methods:

1. Top-down method

The top-down method solves the overall problem before you break it down into subproblems. This process works to solve larger problems by finding the solution to subproblems recursively, caching each result. This process of memorization helps to avoid solving the problem repeatedly if you call it more than once. With the top-down method, you can return the result you save as you solve the overall problem, thus storing the results of problems you've already solved.

Related: Is Computer Programming a Good Career? Definition and Tips

2. Bottom-up method

In the bottom-up method, or tabulation method, you solve all the related sub-problems first instead of applying recursion. As bottom-up tabulation requires multiple solvencies, dynamic programming uses an n-dimensional table, where n represents a value of zero or greater. As you solve each subproblem within the table, you can then use the results to compute the original problem.

 

https://www.geeksforgeeks.org/tabulation-vs-memoization/

There are two different ways to store the values so that the values of a sub-problem can be reused. Here, will discuss two patterns of solving dynamic programming (DP) problems: 
 

1. Tabulation: Bottom Up
2. Memoization: Top Down

 

Tablulation -- 计算阶乘

// Tabulated version to find factorial x.
int dp[MAXN];

// base case
int dp[0] = 1;
for (int i = 1; i< =n; i++)
{
    dp[i] = dp[i-1] * i;
}

 

Memoization -- 计算阶乘

// Memoized version to find factorial x.
// To speed up we store the values
// of calculated states

// initialized to -1
int dp[MAXN]

// return fact x!
int solve(int x)
{
    if (x==0)
        return 1;
    if (dp[x]!=-1)
        return dp[x];
    return (dp[x] = x * solve(x-1));
}

 

 

Simple DEMO

https://web.stanford.edu/class/cs97si/04-dynamic-programming.pdf

 

 

 

 

 

 

 

 

 

SHORT PATH LECTURE

https://people.eecs.berkeley.edu/~vazirani/algorithms/chap6.pdf

 

WHY IS IT CALLED DYNAMIC PROGRAMMING?

Direct Source

 Bellman博士给自己的研究命名， 让他的工作开起来不是纯数学研究， 同时也不至于太过于没有技术含量。

 

https://www.quora.com/Why-is-dynamic-programming-called-dynamic-programming

Paraphrasing from Dr.Richard Bellman’s biography excerpt

:

Dr. Bellman wanted to pick a term that didn’t sound like mathematical research. The Secretary of Defense was biased against research. He also did not want a term that could be used in a pejorative (derogatory) sense.

So he picked “programming”, which sounded less like mathematical research. He also wanted to get across the idea that it was multistage, so he picked “dynamic”. This was also hard to use in a negative way.

The term was coined so that no one would object to it and Dr. Bellman would continue his work.

 

 什么是Dynamic PROGRAMMING?

https://www.quora.com/What-is-the-difference-between-dynamic-programming-and-linear-programming

此处Promgraming不是编码的意思， 翻译过来是规划的含义， 相同的术语有 整数规划（Integer Program），也有翻译成整数优化。

例如你的人生有什么规划：

第一步xxxx

第二步yyyy

第三步zzzz

还有类似：春节晚会排练的规划

但是这种规划一般都是静态的， 每一个stage做什么事情一目了然。

 

动态规划，其生成的规划表， 是随着stage动态变化的，因为其需要考虑新stage带来的变化。

这里实际上就是一个数学模型，术语运筹学范畴，对资源的使用进行管理，并且是随着stage变化（新的stage带有新的输入）资源的使用也做动态调整。

 

At first, “programming” has nothing to do with writing code.

It simply means filling up a table, like in making a TV/radio schedule. A deliberately missing term is “mathematical model” in the very end of it (RAND Corporation and US Government had issues with that).

Replace “programming” with “resource management” to get a precise meaning.

Replace the fad word “dynamic” with a choice from three precise words, “temporal”, “sequential”, or “serial” (meaning unfolding in time, as a sequence).

The world “linear” comes from abstract vector spaces which are linear. It’s the same word as in “linear algebra”. A more meaningful words for “linear” are “structure-preserving”, “homomorphic”, “shape-preserving”.

Now we can finally be able to compare:
“Sequential resource management model” vs “Shape-preserving resource management model”. Sounds quite specific, isn’t it?

 

当前决策是依赖之前已经做过的决策。

In a dynamic program, we want to make a series of decisions in such a way as to maximize some function. The key is that the set of decisions available to us at any given time depends on what we have already decided to do previously. The simplest example I know of is the optimal consumption and saving

 

https://www.quora.com/What-is-dynamic-programming

动态规划考虑的问题元素是有限定的， 每一个问题都依赖一定的变量， 则每一个stage决策可以看做是一个问题，为其求解最优解， 需要参考之前的stage的最优解，这里就产生的嵌套。

Recursion without repetition.

For more details, see Chapter 3

of my algorithms book.

 

动态规划 -- 无后效性

https://www.cnblogs.com/qilinart/articles/9739051.html

无后效性是一个问题可以用动态规划求解的标志之一，理解无后效性对求解动态规划类题目非常重要

某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响

 

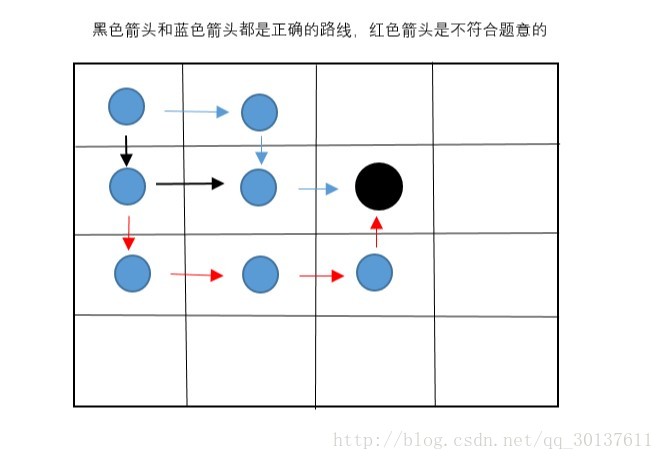
假设棋子走到了第二行第三列，记为s(2,3),如下图，画了两条路线和一条不符合题意的路线，那么当前的棋子[s(2,3)位置]怎么走到右下角和之前棋子是如何走到s(2,3)这个位置无关[不管是黑色尖头的路线还是蓝色箭头的路线]
换句话说，当位于s(2,3)的棋子要进行决策（向右或者向下走）的时候，之前棋子是如何走到s(2,3)这个位置的是不会影响我做这个决策的。之前的决策不会影响了未来的决策（之前和未来相对于现在棋子位于s(2,3)的时刻），这就是无后效性,也就是所谓的“未来与过去无关”

 

看完了无后效性，那我们再来看看有后效性，还是刚才的例子，只不过现在题目的条件变了，现在棋子可以上下左右走但是不能走重复的格子

那么现在红色箭头就是一个合法的路线了，当我的棋子走到了s(2,3)这个位置的时候，要进行下一步的决策的时候，这时候的决策是受之前棋子是如何走到s(2,3)的决策的影响的，比如说红色箭头的路线，如果是红色箭头决策而形成的路线，那么我下一步决策就不能往下走了[因为题意要求不能走重复的格子]，之前的决策影响了未来的决策，”之前影响了未来”,这就叫做有后效性

https://segmentfault.com/a/1190000040379204

可能你还是对什么是“无后效性”问题感到难以理解。没关系，我们再举一个更具象的例子，这是 LeetCode 62. Unique Paths ：给定一个 的矩阵，从左上角作为起点，到达右下角共有多少条路径（机器人只能往右或者往下进行移动）。

这是一道经典的「动态规划」入门题目，也是一个经典的“无后效性”问题。

它的“无后效性”体现在：当给定了某个状态（一个具体的 的矩阵和某个起点，如 (1,2)），那么从这个点到达右下角的路径数量就是完全确定的。

而与如何到达这个“状态”无关，与机器人是经过点 (0,2) 到达的 (1,2)，还是经过 (1,1) 到达的 (1,2) 无关。

这就是所谓的“无后效性”问题。