树状数组

树状数组运用了二进制分解原理

对于任意的整数x，都可以分解为：$x=2^{i_1}+2^{i_2}+...+2^{i_m}$
其中$i_1>i_2>...>i_m$
于是可以把$[1,x]$分解成很多段
$[1,2^{i_1}]$
$[2^{i_1}+1,2^{i_1}+2^{i_2}]$
$[2^{i_1}+2^{i_2}+1,2^{i_1}+2^{i_2}+2^{i_3}]$
. . .
$[2^{i_1}+2^{i_2}+...+2^{i_{m-1}}+1,2^{i_1}+2^{i_2}+...+2^{i_m}]$

比如$7=4+2+1$
于是$[1,7]=[1,4]+[5,6]+[6,7]$
定于 $lowbit(x)$ 表示 $x$ 在 $2$ 分解下最小的幂
$lowbit(7)=1,lowbit(6)=2,lowbit(4)=4$
公式：$lowbit(x)=x\&-x$

树状数组：维护序列前缀和
$c[x]$ 表示区间 $[x-lowbit(x)+1,x]$ 之间的数的和

如图

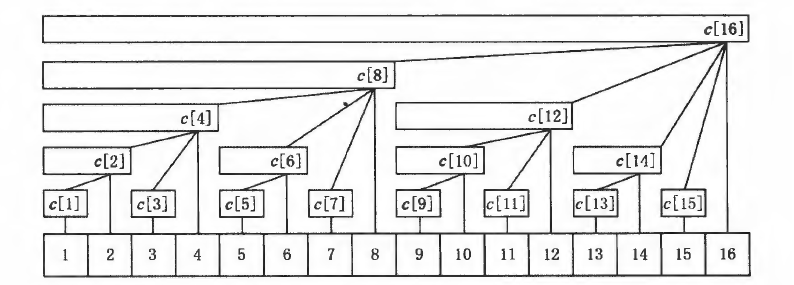
其中 $c[x]$ 的父亲节点是 $c[x+lowbit(x)]$

逆序对：$i>j$ 但 $a_i<a_j$

树状数组求逆序对：
其实树状数组只不过是动态维护前缀和并随时查询 $[1,a[i]-1]$罢了
逆序扫一遍就可以求得了

for (int i = n; i >= 1; i--) {
	r[i] = ask(a[i] - 1) ;
	add(a[i]) ;
}

楼兰图腾：求三个数满足单峰型 $(132)$ 和逆单峰型 $(312)$
对于单峰型：对于每个 $i$，只需要查询 $i$ 之前的小于 $a_i$ 的和 $i$ 之后小于 $a_i$ 的即可
前者正序扫一遍求后者逆序扫一遍求

对于逆单峰型，其实是单峰型的倒置
只需要处理数组是 $a_i=n+1-a_i$ 即可

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std ;

typedef long long ll ;
const int N = 200010 ;

int n ;
int a[N], l[N], r[N], c[N] ;
vector <ll> res ;

void add(int x) {
	for (; x <= n; x += x & -x) c[x] += 1 ;
}

int ask(int x) {
	int t = 0 ;
	for (; x; x -= x & -x) t += c[x] ;
	return t ;
}

void work() {
	for (int i = n; i >= 1; i--) {
		r[i] = ask(a[i] - 1) ;
		add(a[i]) ;
	}
	memset(c, 0, sizeof(c)) ;
	for (int i = 1; i <= n; i++) {
		l[i] = ask(a[i] - 1) ;
		add(a[i]) ;
	}
	ll ans = 0 ;
	for (int i = 1; i <= n; i++) ans += 1ll * l[i] * r[i] ;
	res.push_back(ans) ;
	memset(c, 0, sizeof(c)) ;
}

int main() {
	scanf("%d", &n) ;
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]) ;
	work() ;
	for (int i = 1; i <= n; i++) a[i] = n - a[i] + 1 ;
	work() ;
	printf("%lld %lld\n", res[1], res[0]) ;
}

树状数组因为是单点修改的一些操作不是太方便

区间修改：将某区间每一个数加上 $x$

因为树状数组是维护动态前缀和，所以可以考虑使用查分使原有的 $a_i=\sum\limits_{j=1}^ib_j$

对于 $[l,r] + x$ 即 $b[l]+x,b[r+1]-x$

用树状数组维护 $b$即可

区改单查

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std ;

typedef long long ll ;
const int N = 1000010 ;

int n, q ;
int a[N], bt[N] ;

int ask(int x) {
	int ans = 0 ; 
	for (; x; x -= x & -x) ans += bt[x] ;
	return ans ;
}

void add(int x, int c) {
	for (; x <= n; x += x & -x) bt[x] += c ;
} 

int main() {
	scanf("%d%d", &n, &q) ;
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]) ;
	while (q--) {
		int op ; scanf("%d", &op) ;
		if (op == 1) {
			int l, r, c ; scanf("%d%d%d", &l, &r, &c) ;
			add(l, c) ; add(r + 1, -c) ;
		} else {
			int x ; scanf("%d", &x) ;
			printf("%d\n", a[x] + ask(x)) ;
		}
	}
}

区间查询

对 $[l,r]$ 查询就查 $[1,r]-[1,l-1]$

区查区改

区改->查分数组 $b$
对于区间查询(x)其实是 $\sum\limits_{i=1}^x \sum\limits_{j=1}^ib_j $

考虑 $b_i$ 的贡献其实是 $x+1-i$ 次

所以上式等价于 $\sum\limits_{i=1}^x (x+1-i)*b_i $
分离常数 $x$ 后 $ = (x+1)*\sum\limits_{i=1}^x b_i - \sum\limits_{i=1}^x i*b_i$
于是需要额外处理 $i*b_i$ 的前缀查询，需要第二个树状数组

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std ;

typedef long long ll ;
const int N = 100010 ;

int n, q ;
int a[N] ;
ll sum[N], bt[2][N] ;

char get() {
	char t = getchar() ;
	while (!isalpha(t)) t = getchar() ;
	return t ;
}

void add(int t, int x, ll c) {
	for (; x <= n; x += x & -x) bt[t][x] += c ;
}

ll ask(int t, int x) {
	ll ans = 0 ; 
	for (; x; x -= x & -x) ans += bt[t][x] ;
	return ans ;
}

ll query(int x) {
	return sum[x] + 1ll * (x + 1) * ask(0, x) - ask(1, x) ;
}

int main() {
	scanf("%d%d", &n, &q) ;
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]), sum[i] = sum[i - 1] + a[i] ;
	while (q--) {
		char op ; op = get() ;
		if (op == 'C') {
			int l, r, c ; scanf("%d%d%d", &l, &r, &c) ;
			add(0, l, c) ; add(1, l, 1ll * l * c) ;
			add(0, r + 1, -c) ; add(1, r + 1, 1ll * (r + 1) * (-c)) ;
		} else {
			int l, r ; scanf("%d%d", &l, &r) ;
			printf("%lld\n", query(r) - query(l - 1)) ;
		}
	}
}

Lost Cows
题意：已知对于每个位置上的数前面有几个比他小，求排列
Sample : # 1 2 1 0 （a）
Answer : 2 4 5 3 1

根据样例的构造发现：
首先最后一个是最好构造的就是$a_i+1$
对于倒数第二个，是剩余的可选项中第$a_i+1$小的
于是就是动态查找第k小

构造b（01序列）存储那个取过

思1：结合二分查找那个第k小的位置 $O(log^2n)$
思2：结合倍增
倍增有个优势，每次只涨2的整数幂次，于是正好对应树状数组中一段数值区间
从大向小的跳，找到那个节点，因为省去查找时间，效率比二分省一个$log$

//二分
int n ;
int a[N], b[N], c[N], res[N] ;

int ask(int x) {
	int ans = 0 ; 
	for (; x; x -= x & -x) ans += c[x] ;
	return ans ;
}

void mdf(int x, int z) {
	for (; x <= n; x += x & -x) c[x] += z ;
} 

int main() {
	scanf("%d", &n) ;
	for (int i = 2; i <= n; i++) scanf("%d", &a[i]) ;
	for (int i = 1; i <= n; i++) mdf(i, 1) ;
	for (int i = n; i >= 1; i--) {
		int p = a[i] + 1, t = 0, l = 1, r = n ;
		while (l <= r) {
			int mid = (l + r) / 2 ;
			int z = ask(mid) ;
			if (z == p) {
				if (z == ask(mid - 1) + 1) {
					t = mid ;
					break ;
				} else {
					r = mid - 1 ;
				}
			}
			else if (z < p) l = mid + 1 ;
			else r = mid - 1 ; 
		}
		res[i] = t ;
		mdf(t, -1) ;
	}
	for (int i = 1; i <= n; i++) printf("%d\n", res[i]) ;
}

//倍增
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std ;

typedef long long ll ;
const int N = 1000010 ;

int n ;
int a[N], c[N], res[N] ;

void mdf(int x, int z) {
	for (; x <= n; x += x & -x) c[x] += z ;
} 

int main() {
	scanf("%d", &n) ;
	for (int i = 2; i <= n; i++) scanf("%d", &a[i]) ;
	for (int i = 1; i <= n; i++) mdf(i, 1) ;
	for (int i = n; i >= 1; i--) {
		int ans = 0, sum = 0 ;
		for (int j = log(n) / log(2); j >= 0; j--) {
			int len = int(pow(2, j)) ;
			if (ans + len <= n && sum + c[ans + len] <= a[i]) {
				sum += c[ans + len] ; ans += len ;
			}
		}
		res[i] = ans + 1 ;
		mdf(res[i], -1) ;
	}
	for (int i = 1; i <= n; i++) printf("%d\n", res[i]) ;
}

posted @ 2023-08-13 22:28 哈奇莱特阅读(12) 评论(0) 收藏举报

刷新页面返回顶部

哈奇莱特

凡心所向，素履以往，生如逆旅，一苇以航。

树状数组

公告