目录
概率
概率是对某一事件发生可能性的数据度量。我们用概率描述事情发生可能性的大小。
试验、计数法则和概率分配
试验:产生明确结果的过程。在一次试验中,有且只有一种结果。
| 试验 |
试验结果 |
| 抛一枚硬币 |
正面、反面 |
| 检测一枚零件 |
合格、不合格 |
| 进行一次销售 |
成功、不成功 |
| 抛掷一枚色子 |
1、2、3、4、5、6 |
样本空间:所有可能的试验结果的集合。
样本点:一次试验的结果。
计数法则、组合和排列
若一个试验的结果可以分为\(k\)步,每一步有\(n_k\)种结果,则所有可能的结果总数为\(\prod n_k\)。
例如,抛掷一枚硬币5次,共有\(2^5\)种结果。
从N项中选取n项的组合数为
\[C_N^n=\frac{N!}{(N-n)!n!}
\]
其中,\(N! = N(N-1)(N-2)…1\)
\(n!=n(n-1)(n-2)…1\)
!为阶乘。
组合数法则基于这样一个场景,对\(N\)个不同单位进行排序,第一个位置有\(N\)种选择,第二个位置有\(N-1\)个,由分布试验计数法则可知,共\(N!\)种结果。考虑另一种选法,将单位分为两部分排序,首先从\(N\)个单位中选出\(n\)个单位用于填补前\(n\)个位置,共有\(C_N^n\)种选择方法,剩余单位用于填补剩余的\(N-n\)个位置,对两部分进行排序,分别为\(n!\)和\((N-n)!\)种结果,由分步计数法则可知,总共\(C_N^nn!(N-n)!\)种结果。因此有
\[N! = C_N^n(N-n)!n!
\]
从N项中选取n项的组合数为
\[A_N^n = \frac {N!} {(N-n)!}
\]
排列数基于这样一个场景,从\(N\)项中首先选择\(n\)项组合数,共\(C_N^n\)种,然后对选出的n种进行排序,共\(n!\)种,由分布计数法则,有
\[A_N^n =C_N^nn!=\frac {N!}{(N-n)!}
\]
概率分配
每种试验结果具有相同的概率,如投硬币,掷色子等。
以大量试验的频率作为概率。
搞笑的
事件及其概率
- 事件:样本的集合。如掷色子获得偶数,掷硬币5次获得3次正面向上。
- 事件的概率:样本点概率之和。
概率的基本性质
事件的补
- 事件A的补:不包括在事件A中的样本点,记为\(\bar A\)
- 概率:\(P(A)=1-P(\bar A)\)
加法公式
- 事件A和B的并:属于A或者属于B的样本点构成的集合,记作\(A\bigcup B\)
- 事件A和B的交:同时属于A和B的样本点构成的集合,记作\(A\bigcap B\)
加法公式:
\[P(A\bigcup B)=P(A)+P(B)-P(AB)
\]
条件概率
- 条件概率:在事件A发生的情况下,事件B发生的概率,记为\(P(B|A)\)
\[P(B|A)=\frac {P(AB)}{P(A)}
\]
- 独立事件:事件A、B的发生互不影响,则AB互为独立事件,有以下充要条件:
\[P(A|B)=P(A)\]
或
\[P(AB)=P(A)P(B)
\]
贝叶斯定理
\[P(A)=\sum P(B_i)P(A|B_i)
\]
其中,事件组B为样本空间的一个分割。
举个例子,求某次考试某班级考试的总合格率,可以用男生合格率乘以男生概率加上女生合格率乘以女生概率。
\[P(A_i|B) = \frac {P(A_i)P(B|A_i)}{\sum_{j=1}^{n} P(A_j)P(B|A_j)}
\]
贝叶斯定理是将全概率公式与条件概率公式结合得到的一个常用的定理。
随机变量及其分布
如抛掷十次硬币,正面朝上的次数\(X\)是随机变量;某十字路口一定时间内经过的汽车的数量是随机变量。
- 离散型随机变量:随机变量的取值范围是离散的数据的变量。
如掷色子的点数只能是1,2,3,4,5,6。
- 连续型随机变量:随机变量的取值范围是连续的区间的变量。
如某人从家里到公司所用的时间。
随机变量的概率分布
\[F(x)=P(X\leq x)
\]
为随机变量的分布函数。
- 分布列:离散型随机变量的分布列指的是随机变量取不同值的概率。其基本条件为:
\[0\leq P(A_i)
\]
\[\sum P(A_i)=1
\]
- 概率密度函数:连续型随机变量的概率密度函数定义如下:
设某连续型随机变量的分布函数为\(F(x)\),若存在实数轴上的一个非负可积函数\(f(x)\),满足
\[F(x)=\int_{-\infty }^{x }f(t)dt
\]
则称\(f(x)\)为该随机变量的概率密度函数。
显然,概率密度函数符合相同的基本条件:
\[f(x)\geq 0
\]
\[\int_{-\infty}^{\infty}f(x)dx=1
\]
对于离散型随机变量而言,概率直接由分布列给出,对于连续型随机变量而言,概率由概率密度函数在某区间上的积分给出,这一点容易用分布函数证明。
数学期望与方差
期望
\[EX=\sum X_iP(X_i)
\]
若级数\(EX\)不收敛,则称期望不存在。
\[EX = \int_{-\infty}^{\infty} xf(x)dx
\]
方差与标准差
\[DX=Var(X)=E(X-EX)^2
\]
\[DX=\sum (X_i-EX)^2P(X_i)
\]
\[DX = \int_{-\infty}^{\infty}(x-EX)^2f(x)dx
\]
\[\sigma=\sqrt{DX}
\]
-
方差的性质
证明:
\[\begin {split}DX &= E(X-EX)^2\\&=E[X^2-2XEX+(EX)^2]\\&=EX^2-2EXEX+(EX)^2\\&=EX^2-(EX)^2\end{split}
\]
- 若c为常数,则\(D(c)=0\)
- 若a,b为常数,则\(D(aX+b)=a^2DX\)
证明:
\[\begin {split} D(aX+b)&=E(aX+b)^2-[E(aX+b)]^2\\&=E(a^2X^2+2abX+b^2)-(aEX+b)^2\\&=a^2EX^2+2abEX+b^2-a^2(EX)^2-2abEX-b^2\\&=a^2[EX^2-(EX)^2]\\&=a^2DX\end{split}
\]
- \(DX=0\Leftrightarrow P(x=a)=1\)
常用离散分布
二项分布
\[P(X=k)=C_n^kp^k(1-p)^{n-k}
\]
记为\(X\sim B(n,p)\)
首先从\(n\)次试验中选出\(k\)次,然后计算\(k\)次试验成功与\((n-k)\)次试验失败的概率。
二项分布的概率恰好为二项式\([p+(1-P)]^n\)中的第\(k+1\)项,二项分布由此得名。
\[E(X)=np
\]
证明:
\[\begin {split}E(X) &= \sum_{k=0}^{n} kP(X=k)\\&=\sum_ {k=1}^n kC_n^kp^k(1-p)^{n-k}\\&=np\sum_ {k=1}^n\frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1}(1-p)^{n-1-(k-1)}\\&=np\sum_{k=1}^{n}C_{n-1}^{k-1}p^{k-1}(1-p)^{n-1-(k-1)}\\&=np(p+1-p)^{n-1}\\&=np\end{split}
\]
\[DX=np(1-p)
\]
证明:
\[\begin {split}DX &= EX^2-(EX)^2\end{split}
\]
\[\begin{split}EX^2&=\sum_{k=0}^{n}k^2P(X=k)\\&=\sum_{k=0}^nk^2C_n^kp^k(1-p)^{n-k}\\&=\sum_{k=1}^nk(k-1+1)C_n^kp^k(1-p)^{n-k}\\&=\sum_{k=2}^nk(k-1)C_n^kp^k(1-p)^{n-k}+\sum_{k=1}^nkC_n^kp^k(1-p)^{n-k}\\&=n(n-1)p^2\sum_{k=2}^nC_{n-2}^{k-2}p^{k-2}(1-p)^{n-2-(k-2)}+np\\&=n(n-1)p^2(p+1-p)^{n-2}+np\\&=n(n-1)p^2+np\end{split}
\]
故
\[DX=n(n-1)p^2+np-(np)^2=np(1-p)
\]
泊松分布
\[P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}(k=0,1,2...)
\]
关于泊松分布概率的由来,可参考以下内容,很通俗易懂的讲解!
泊松分布的现实意义是什么,为什么现实生活多数服从于泊松分布? - 马同学的回答 - 知乎
https://www.zhihu.com/question/26441147/answer/429569625
容易验证,泊松分布的概率和为1:
\[\sum_{k=0}^{n}\frac{\lambda^k}{k!}e^{-\lambda}=e^{-\lambda}\sum_{k=0}^{n}\frac{\lambda^k}{k!}=e^{-\lambda}e^{\lambda}=1
\]
\[\begin{split}EX&=\sum_{k=0}^{\infty}kP(X=k)\\&=\lambda e^{-\lambda}\sum_{k=0}^{\infty}\frac{\lambda^{k-1}}{(k-1)!}\\&=\lambda e^{-\lambda}e^{\lambda}\\&=\lambda\end{split}
\]
\[\begin{split}EX^2&=\sum_{k=0}^{n}k^2P(X=k)\\&=\sum_{k=1}^{\infty}k^2\frac{\lambda^k}{k!}e^{-\lambda}\\&=\sum_{k=1}^{\infty}k(k-1+1)\frac{\lambda^{k}}{k!}e^{-\lambda}\\&=\sum_{k=2}^{\infty}k(k-1)\frac{\lambda^{k}}{k!}e^{-\lambda}+\sum_{k=1}^{\infty}k\frac{\lambda^{k}}{k!}e^{-\lambda}\\&=\lambda^2 e^{-\lambda}\sum_{k=2}^{\infty}\frac{\lambda^{k-2}}{(k-2)!}+\lambda \\&=\lambda^2+\lambda\end{split}
\]
\[DX=EX^2-(EX)^2=\lambda
\]
泊松定理:在n重伯努利试验中,记事件A在一次试验中发生的概率为\(p_n\),若当\(n\rightarrow\infty\)时,有\(np_n\rightarrow\lambda\),则
\[\lim_{n\rightarrow\infty}P(A)=\lim_{n\rightarrow\infty}C_n^kp_n^k(1-p_n)^{n-k}=\frac {\lambda^k}{k!}e^{-\lambda}
\]
证明:
\[\begin{split}\lim_{n\rightarrow\infty}P(A)&=\lim_{n\rightarrow\infty}C_n^kp_n^k(1-p_n)^{n-k}\\&=\lim_{n\rightarrow\infty}\frac{n(n-1)…(n-k+1)}{k!}(\frac{\lambda}{n})^k(1-\frac \lambda n)^{n-k}\\&=\frac{\lambda^k}{k!}\lim_{n\rightarrow\infty}\frac{n(n-1)…(n-k+1)}{n^k}(1-\frac \lambda n)^{n-k} \end{split}
\]
又有
\[\lim_{n\rightarrow\infty}\frac{n(n-1)…(n-k+1)}{n^k}=1
\]
\[\lim_{n\rightarrow\infty}(1-\frac \lambda n)^{n-k}=e^{-\lambda}
\]
故原命题得证
由于泊松定理是在\(np_n\rightarrow\lambda\)的情况下得到的,因此,在实际情况中,当二项分布\(B(n,p)\)试验次数\(n\)很大,概率\(p\)较小,\(\lambda\)适中时,可以使用泊松分布做近似。
超几何分布
考虑这样一个场景,\(N\)件产品中有\(M\)件合格品,从中抽取\(n\)件,其中合格品数量为\(m\)的概率即为超几何分布。
\[P(m)=\frac{C_M^mC_{N-M}^{n-m}}{C_N^n}
\]
\[E(X)=n\frac MN
\]
证明:
\[\begin{split}E(X)&=\sum_{m=0}^{M}m\frac{C_M^mC_{N-M}^{n-m}}{C_N^n}\\&=n\frac MN\sum_{m=1}^{M}\frac{C_{M-1}^{m-1}C_{N-M}^{n-m}}{C_{N-1}^{n-1}}\\&=n\frac MN\end{split}
\]
\[DX=\frac{nM(N-M)(N-n)}{N^2(N-n)}
\]
证明:
\[\begin{split}EX^2 &= \sum_{m=0}^{M}m^2\frac{C_M^mC_{N-M}^{n-m}}{C_N^n}\\&=\sum_{m=1}^{M}m(m-1+1)\frac{C_M^mC_{N-M}^{n-m}}{C_N^n}\\&=\sum_{m=2}^{M}m(m-1)\frac{C_M^mC_{N-M}^{n-m}}{C_N^n}+EX\\&=\frac {M(M-1)n(n-1)}{N(N-1)}+EX\end{split}
\]
\[DX = EX^2 - (EX)^2=\frac{nM(N-M)(N-n)}{N^2(N-1)}
\]
几何分布
- 几何分布:在n重伯努利试验中,事件首次出现的试验次数为\(X\),则\(X\)服从几何分布,记为\(X\sim Ge(p)\)
\[P(X=k)=(1-p)^{k-1}p
\]
令\(q=1-p\)
\[\begin{split}E(X)&=\sum_{k=1}^{\infty}kq^{k-1}p\\&=p\sum_{k=1}^\infty\frac{dq^k}{dq}\\&=p\frac {d\sum_{k=0}^\infty q^k}{dq}\\&=p\frac d{dq}\frac 1{1-q}\\&=\frac p{(1-q)^2}\\&=\frac 1p\end{split}
\]
\[\begin{split}EX^2 &= \sum_{k=1}^\infty k^2q^{k-1}p\\&=p\sum_{k=1}^\infty(k-1+1)kq^{k-1}\\&=pq\sum_{k=1}^\infty k(k-1)q^{k-2}+\frac 1p\\&=pq\sum_{k=1}^\infty \frac{d^2q^k}{dq^2}+\frac 1p\\&= pq \frac{d^2\sum_{k=0}^\infty q^k}{dq^2}+\frac 1p\\&=\frac {2q}{p^2}+\frac 1q\end{split}
\]
\[DX=\frac{1-p}{p^2}
\]
常用连续分布
正态分布
\[f(x)=\frac 1{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\]
则称随机变量X服从正态分布,记为\(X\sim N(\mu,\sigma^2)\),其中\(\mu\)为均值,\(\sigma\)为标准差。
-
标准正态分布:若\(X\sim N(0,1)\),则称X服从于标准正态分布。
-
正态分布的标准化:若\(X\sim N(\mu,\sigma^2)\),则\(T=\frac{X-\mu}{\sigma}\sim N(0,1)\)
证明:设\(X、T\)的分布函数分别为\(F_X(x)、F_T(t)\),概率密度分别为\(f_X(x)、f_T(t)\),则
\[\begin{split}F_T(t)=P(T\leq t)=P(X\leq \sigma t+\mu)=F_X(\sigma t+\mu)\end{split}
\]
\[f_T(t)=F_T'(t)=\sigma f_X(\sigma t+\mu)=\frac 1{\sqrt{2\pi}}e^{-\frac{t^2}{2}}
\]
证明:
\[\begin{split}E(\frac{X-\mu}{\sigma} )=E(T)&=\int_{-\infty}^{\infty}t\frac1{\sqrt{2\pi}}e^{-\frac{t^2}2}dt\end{split}
\]
可以看出被积函数为奇函数,故
\[E(\frac{X-\mu}{\sigma} )=E(T)=0
\]
\[EX=\mu
\]
证明:
\[\begin{split}ET^2&=\int_{-\infty}^{\infty}t^2\frac 1{\sqrt {2\pi}}e^{-\frac {t^2}2}dt\\&=\frac 1{\sqrt{2\pi}}\int_{-\infty}^{\infty}(-t)de^{-\frac {t^2}2}\\&=\frac 1{\sqrt{2\pi}}[-te^{-\frac {t^2}2}|_{-\infty}^{\infty} + \int_{-\infty}^{\infty}e^{-\frac {t^2}2}dt]\\&=1\end{split}
\]
\[DX=D(\sigma T+\mu)=\sigma^2
\]
均匀分布
\[f(x)=\begin{cases}
\frac1{b-a}& \text{a < x < b}\\
0& \text{其他}
\end{cases}\]
指数分布
\[f(x)=\begin {cases}
\lambda e^{-\lambda x} &\text{x >= 0}\\
0 &\text{x < 0}
\end {cases}\]
其中\(\lambda>0\)
\[\begin{split}EX&=\int_0^{+\infty}\lambda xe^{-\lambda x}dx\\&=\int_0^{+\infty}(-x)de^{-\lambda x}\\&=-xe^{-\lambda x}|_0^{+\infty}+\int_0^{+\infty}e^{-\lambda x}dx\\&=\frac 1{\lambda}\end{split}
\]
\[\begin{split}EX^2&=\int_0^{+\infty}\lambda x^2e^{-\lambda x}dx\\&=\int_0^{+\infty}(-x^2)de^{-\lambda x}dx\\&=-x^2e^{-\lambda x}|_0^{+\infty}+\int_0^{+\infty}2xe^{-\lambda x}dx\\&=\frac 2{\lambda^2}\end{split}
\]
\[DX=EX^2-(EX)^2=\frac 1{\lambda^2}
\]
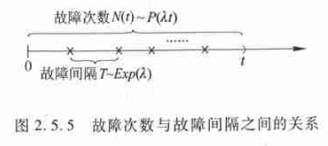
指数分布用于描述某事件连续两次发生之间的时间间隔
![image]()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号