标准差
标准差(英语:Standard Deviation),数学符号σ,在概率统计中最常使用作为统计分布程度(statistical dispersion)上的测量。标准差定义为方差的算术平方根,反映组内个体间的离散程度;标准差与期望值之比为标准离差率。测量到分布程度的结果,原则上具有两种性质:
- 为非负数值;
- 与测量资料具有相同单位。
一个总量的标准差或一个随机变量的标准差,及一个子集合样品数的标准差之间,有所差别。其公式如下所列。
标准差的观念是由卡尔·皮尔逊(Karl Pearson)引入到统计中。
目录
[隐藏]
阐述及应用[编辑]
简单来说,标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合{0, 5, 9, 14}和{5, 6, 8, 9}其平均值都是7,但第二个集合具有较小的标准差。
表述“相差k个标准差”,即在 的样本(Sample)范围内考量。
的样本(Sample)范围内考量。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为如果测量值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
总体的标准差[编辑]
基本定义[编辑]
μ为平均值。
简易口诀:离均差平方和的平均;方均根
简化计算公式[编辑]
上述公式可以如下代换而简化:
所以:
根号里面,亦即方差( )的简易口诀为:“平方的平均”减去“平均的平方”。
)的简易口诀为:“平方的平均”减去“平均的平方”。
总体为随机变量[编辑]
一随机变量 的标准差定义为:
的标准差定义为:
须注意并非所有随机变量都具有标准差,因为有些随机变量不存在期望值。 如果随机变量 为
为 具有相同概率,则可用上述公式计算标准差。
具有相同概率,则可用上述公式计算标准差。
离散随机变量的标准差[编辑]
若 是由实数
是由实数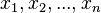 构成的离散随机变量(英语:discrete random variable),且每个值的概率相等,则
构成的离散随机变量(英语:discrete random variable),且每个值的概率相等,则 的标准差定义为:
的标准差定义为:
![\sigma = \sqrt{\frac{1}{N}\left[(x_1-\mu)^2 + (x_2-\mu)^2 + \cdots + (x_N - \mu)^2\right]}]() ,其中
,其中 ![\mu = \frac{1}{N} (x_1 + \cdots + x_N)]()
换成用 来写,就成为:
来写,就成为:
![\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}]() ,其中
,其中 ![\mu = \frac{1}{N} (x_1 + \cdots + x_N)]()
目前为止,与总体标准差的基本公式一致。
然而若每个 可以有不同概率
可以有不同概率 ,则
,则 的标准差定义为:
的标准差定义为:
![\sigma = \sqrt{\sum_{i=1}^N p_i(x_i - \mu)^2}]() ,其中
,其中 ![\mu = \sum_{i=1}^N p_i x_i.]()
连续随机变量的标准差[编辑]
若 为概率密度
为概率密度 的连续随机变量(英语:continuous random variable),则
的连续随机变量(英语:continuous random variable),则 的标准差定义为:
的标准差定义为:
其中
标准差的特殊性质[编辑]
对于常数 和随机变量
和随机变量 和
和 :
:
![\sigma(X+c)=\sigma(X)]()
![\sigma(cX)=c\cdot\sigma(X)]()
![\sigma(X+Y) = \sqrt{ \sigma^2(X) + \sigma^2(Y) + 2\cdot\mbox{cov} (X,Y)}]()
- 其中:
![\mbox{cov}(X,Y)]() 表示随机变量
表示随机变量![X]() 和
和![Y]() 的协方差。
的协方差。
- 其中:
样本的标准差[编辑]
在真实世界中,找到一个总体的真实的标准差是不现实的。大多数情况下,总体标准差是通过随机抽取一定量的样本并计算样本标准差估计的。
从一大组数值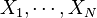 当中取出一样本数值组合
当中取出一样本数值组合 ,常定义其样本标准差:
,常定义其样本标准差:
样本方差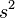 是对总体方差
是对总体方差 的无偏估计。
的无偏估计。 中分母为
中分母为 (相较于总体
(相较于总体 中的分母为
中的分母为 ),是因为
),是因为 的自由度为
的自由度为 ,这是由于存在约束条件
,这是由于存在约束条件 。
。
范例[编辑]
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为{ 5, 6, 8, 9 }:
- 第一步,计算平均值
![\overline{x}]() ︰
︰
- 当
![\begin{smallmatrix}N = 4\end{smallmatrix}]() (因为集合里有4个数),分别设为:
(因为集合里有4个数),分别设为:
![\overline{x}= 7]() (此为平均值)
(此为平均值)
- 第二步,计算标准差
![\sigma\,]() ︰
︰
![\sigma = 1.5811\,\!]() (此为标准差)
(此为标准差)
正态分布的规则[编辑]
在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约68%数值分布在距离平均值有1个标准差之内的范围,约95%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”。
标准差与平均值之间的关系[编辑]
一组数据的平均值及标准差常常同时作为参考的依据。从某种意义上说,如果用平均值来考量数值的中心的话,则标准差也就是对统计的分散度的一个“自然”的测度。因为由平均值所得的标准差要小于到其他任何一个点的标准差。较确切的叙述为:设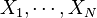 为实数,定义函数
为实数,定义函数
使用微积分或者通过配方法,不难算出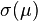 在下面情况下具有唯一最小值:
在下面情况下具有唯一最小值:
几何学解释[编辑]
从几何学的角度出发,标准差可以理解为一个从 维空间的一个点到一条直线的距离的函数。举一个简单的例子,一组数据中有3个值,
维空间的一个点到一条直线的距离的函数。举一个简单的例子,一组数据中有3个值,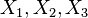 。它们可以在3维空间中确定一个点
。它们可以在3维空间中确定一个点 。想像一条通过原点的直线
。想像一条通过原点的直线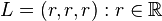 。如果这组数据中的3个值都相等,则点
。如果这组数据中的3个值都相等,则点 就是直线
就是直线 上的一个点,
上的一个点, 到
到 的距离为0,所以标准差也为0。若这3个值不都相等,过点
的距离为0,所以标准差也为0。若这3个值不都相等,过点 作垂线
作垂线 垂直于
垂直于 ,
, 交
交 于点
于点 ,则
,则 的坐标为这3个值的平均数:
的坐标为这3个值的平均数:
运用一些代数知识,不难发现点 与点
与点 之间的距离(也就是点
之间的距离(也就是点 到直线
到直线 的距离)是
的距离)是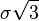 。在
。在 维空间中,这个规律同样适用,把
维空间中,这个规律同样适用,把 换成
换成 就可以了。
就可以了。




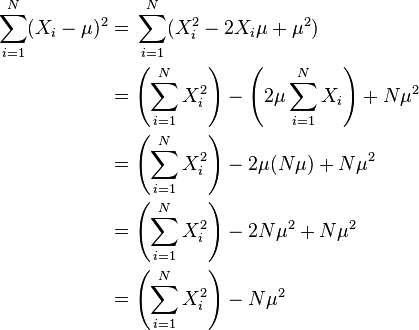

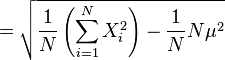
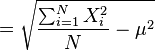

![\sigma = \sqrt{\frac{1}{N}\left[(x_1-\mu)^2 + (x_2-\mu)^2 + \cdots + (x_N - \mu)^2\right]}](http://upload.wikimedia.org/math/5/f/d/5fd5ad66a1ae1ee408268b16d163432d.png) ,其中
,其中 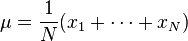
 ,其中
,其中 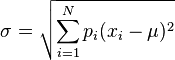 ,其中
,其中 
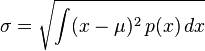
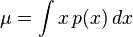
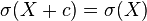
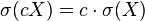
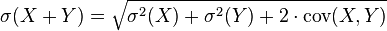
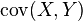 表示随机变量
表示随机变量
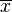 ︰
︰
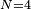 (因为集合里有4个数),分别设为:
(因为集合里有4个数),分别设为: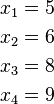
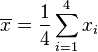
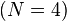
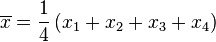
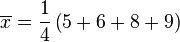
 (此为平均值)
(此为平均值)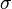 ︰
︰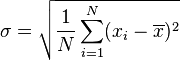

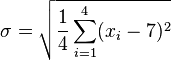
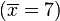
![\sigma = \sqrt{\frac{1}{4} \left [ (x_1 - 7)^2 + (x_2 - 7)^2 + (x_3 - 7)^2 + (x_4 - 7)^2 \right ] }](http://upload.wikimedia.org/math/1/b/3/1b3ee6d89f69664070242d56103f30b0.png)
![\sigma = \sqrt{\frac{1}{4} \left [ (5 - 7)^2 + (6 - 7)^2 + (8 - 7)^2 + (9 - 7)^2 \right ] }](http://upload.wikimedia.org/math/6/2/c/62c241b9f368cfa8d1d37b0a53950a55.png)



 (此为标准差)
(此为标准差)
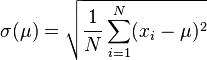

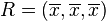

 浙公网安备 33010602011771号
浙公网安备 33010602011771号