tanh函数即它的导数

tanh函数（双曲正切函数）是神经网络中一种常用的激活函数，它的数学表达式为：

它的输出范围是 (-1, 1)。

tanh函数的特点

• 非线性：和 Sigmoid 函数一样，tanh 函数也是非线性的，这使得它能够为神经网络引入非线性特性，从而学习和解决更复杂的问题。
• 对称性：tanh 函数关于原点对称，它的中心在 $(0, 0)$。这意味着当输入为正时，输出为正；当输入为负时，输出为负。这有助于模型更好地处理负向输入，使得数据的平均值更接近 0，从而加快模型的收敛速度。
• 梯度消失问题：与 Sigmoid 函数类似，当输入 $x$ 的值非常大或非常小时（例如 $x > 2$ 或 $x < -2$），tanh 函数的梯度（导数）会变得非常接近于 0。这会导致在反向传播过程中，梯度被反复相乘后变得非常小，使得靠近输入层的权重更新非常缓慢，即梯度消失问题。

tanh函数与Sigmoid函数的比较

特性	tanh函数	Sigmoid函数
数学表达式
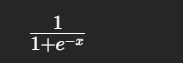输出范围	(-1, 1)	(0, 1)
优点	中心在0，使得训练收敛更快。	输出范围为 (0, 1)，常用于二分类模型的输出层。
缺点	梯度消失问题。	梯度消失问题；输出不以0为中心，可能影响收敛速度。

在早期的神经网络中，tanh 函数因为其以 0 为中心的特性，通常比 Sigmoid 函数更受欢迎，因为它能有效缓解 Sigmoid 函数中非零中心化带来的问题。

在代码中如何实现

你可以使用 NumPy 轻松实现 tanh 函数：

import numpy as np

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

在实际应用中，由于 np.tanh 函数经过了底层优化，你通常可以直接调用它来获得更好的性能和数值稳定性：

import numpy as np

def tanh(x):
    return np.tanh(x)

tanh 函数的导数非常简洁，它的导数是：

---

在代码中如何实现

在反向传播中，你需要计算 tanh 的梯度。由于你已经在前向传播中计算了 tanh(x) 的结果，你可以直接利用这个结果来计算梯度，而不需要重新计算 e^x 和 e^{-x}，这会提高效率。

import numpy as np

# 假设你在前向传播中已经计算了 tanh(x) 的结果
result = np.tanh(x)

# 反向传播时计算梯度
# G是上一层传递回来的梯度
grad_output = G * (1 - result**2)