DoubleLi

qq: 517712484 wx: ldbgliet
  博客园 :: 首页 :: 新随笔 :: 联系 :: 订阅 :: 管理 ::
二叉树及其三种遍历

一.二叉树的常用性质

1.常用性质

<1>.在二叉树的第i层上最多有2^(i-1) 个节点 。（i>=1）

<2>.二叉树中如果深度为k(有k层),那么最多有2^k-1个节点。(k>=1）

<3>.若二叉树按照从上到下从左到右依次编号，则若某节点编号为k，则其左右子树根节点编号分别为2k和2k+1;

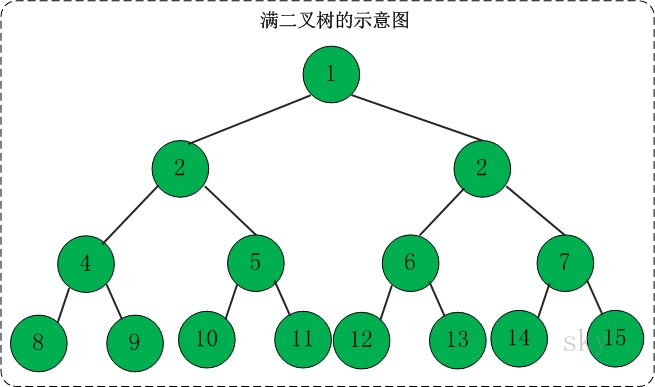
<4>.二叉树分类：满二叉树，完全二叉树

满二叉树：高度为h，由2^h-1个节点构成的二叉树称为满二叉树。

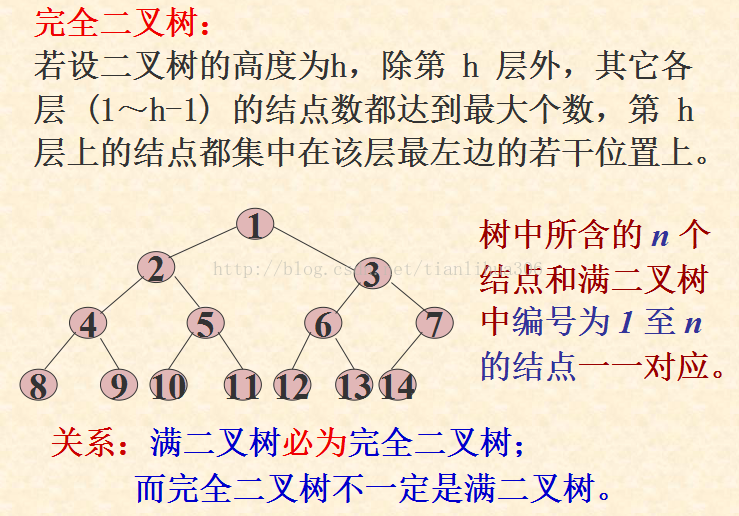
<5>.在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]+1是向下取整。满二叉树的深度为k=log2(n+1);

 

2.例题 （求解二叉树的循环递归规律法）

例题：uva679 小球下落

题意：有一颗满二叉树，每个节点是一个开关，初始全是关闭的，小球从顶点落下，小球每次经过开关就会把它的状态置反，这个开关为关时，小球左跑，为开时右跑。现在问第k个球下落到d层时的开关编号。输入深度d和小球个数k。d<20，k<524288

思路分析：首先该题最先想到的是模拟，开一个数组表示开关，下标表示编号，根据k的子树为2k和2k+1来改变数组，判断进行。但是该思路不但要开2^20这么大的数组而且循环最大时有524288*2^20次，绝对超时！

因此改变思路，寻找题目规律：

<1>.首先对于每一层，第奇数个落入该层的球都是往左走的，第偶数个落入该层的球都是往右走的。

<2>.因为小球都是按照编号依次下落的，对于左枝（也就是奇数球)，每个I号小球落入该层都是第(I+1)/2个小球。而偶数是往右走的I/2个小球！

<3>.因此每一层循环递归，来判断i，循环d层，即可找出最后叶子！省去大数组和大时间

代码：

  1. #include <iostream>
  2. #include<cstdio>
  3. using namespace std;
  4. int main()
  5. {
  6.     int n;
  7.     while(cin>>n)
  8.     {
  9.         if(n==-1)break;
  10.         int D,I;
  11.         while(n--)
  12.         {
  13.             cin>>D>>I;//D层I个小球
  14.             int k=1;
  15.             for(int i=0; i<D-1; i++)
  16.             {
  17.                 if(I%2)//奇数是往左走的第（i+1)/2个小球
  18.                 {
  19.                     k=k*2;//往左走是k*2
  20.                     I=(I+1)/2;//改变小球
  21.                 }
  22.                 else
  23.                 {
  24.                     k=(k*2+1);//偶数是往右走的第（i/2）个小球
  25.                     I=I/2;
  26.                 }
  27.             }
  28.             cout<<k<<endl;
  29.         }
  30.     }
  31.     return 0;
  32. }

 

二叉树的实现方式

1.第一类数组实现

  用数组root[]存储结点值，在这种实现当中，对于编号为k的节点，其左子节点的编号为2*k，右子节点的编号为2*k + 1，另外确定根节点的编号为1.毫无疑问，这种实现极易产生巨大的空间浪费，比如对于一个只有一条链的树，假设该树含有31个节点，存储这31个节点却需要开一个2^30的数组，因此此方法较少使用。（此处的2^30是指数值，由2k计算出来的数值过大）

2.结构体+指针实现

  用结构体指针u来表示一个节点，其中u->v表示该节点的权值，u->left和u->right分别指向该节点的左右子节点，初始化全部为NULL，若需用到该节点，则申请空间，否则视为无子节点！就这样互相联系成一颗结构体指针二叉树！节省空间，但是容易出现指针悬挂或者未知的指针内存错误。

3..第二类数组实现

  对于一棵有n个节点树，只需要开一个大小为n的数组，节点按照出现顺序依次编号，这么一来，每个节点的左右节点的编号就无法通过2*k，2*k+1的形式来直接确定了，这时就需要数组lch[maxn] , rch[maxn]；其中lch[u]表示u节点的左子节点的编号，因此通过u = lch[u]就可以访问到u节点的左子节点，rch[u]的含义同理。另外，用value[u]表示编号为u节点的权值，如此一来，申请新节点的newnode函数与初始化的newtree函数写法就变得不同了，具体见代码。（此处只需结点个数个数组即可，并不计算数值！）

 

4.例题：uva122 树的层次遍历

题意：给你一颗二叉树，按照从上到下从左到右的顺序输出每个节点的权值，若某个节点没有赋值或者输入超过一次，则输出no complete.

输入：(11,LL) (7,LLL) (8,R)
(5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()

输出：5 4 8 11 13 4 7 2 1
not complete

<1>.结构体指针实现法

第一步解决输入问题建树，然后递归遍历树模拟判断即可！

代码：

  1. #include <iostream>
  2. #include<cstdio>
  3. #include<vector>
  4. #include<queue>
  5. #include<cstring>
  6. using namespace std;
  7. const int maxn=266;
  8. char s[maxn];//输入
  9. bool failed;
  10. struct Node//节点
  11. {
  12.     bool have_value;//该点是否被赋值过
  13.     int v;//该点权值
  14.     Node*left,*right;//左右子节点
  15.     Node():have_value(false),left(NULL),right(NULL){}//初始化函数
  16. };
  17. Node*root;//树根！！
  18. Node* newnode()//分配内存
  19. {
  20.     return new Node();//分配同时初始化
  21. }
  22. void addnode(int v,char *a)//建树
  23. {
  24.     int len=strlen(a);
  25.     Node *u=root;
  26.     for(int i=0;i<len;i++)
  27.     {
  28.         if(a[i]=='L')//左
  29.         {
  30.             if(u->left==NULL)u->left=newnode();//若左节点没有分配内存，没有开辟过，则申请内存，因为经过该节点了，该节点必须赋值！
  31.             u=u->left;//更新路径
  32.         }
  33.         else if(a[i]=='R')//右
  34.         {
  35.             if(u->right==NULL)u->right=newnode();//同上
  36.             u=u->right;
  37.         }
  38.     }
  39.     if(u->have_value)failed=true;//如果该节点已经被赋值过了，则非法输入，报错
  40.     u->v=v;//更新该节点
  41.     u->have_value=true;//标记赋值
  42. }
  43.  
  44. bool read_in()//输入
  45. {
  46.     root=newnode();//给树根申请内存
  47.     failed=false;//标记
  48.     for(;;)
  49.     {
  50.         if(scanf("%s",s)!=1)return false;//输入c+z了结束
  51.         if(strcmp(s,"()")==0)break;//读到()表示该组数据正常结束
  52.         int v;
  53.         sscanf(&s[1],"%d",&v);//sscanf读取权值并赋给v
  54.         addnode(v,strchr(s,',')+1);//读取路径，并且建树，最好不要在此处判断failed因为还没有完整输入数据
  55.     }
  56.     return true;
  57. }
  58. bool bfs(vector<int>&ans)//遍历树，并保存权值
  59. {
  60.     queue<Node*>q;//队列
  61.     ans.clear();
  62.     q.push(root);
  63.     while(!q.empty())
  64.     {
  65.         Node*u=q.front();
  66.         q.pop();
  67.         if(!u->have_value)return false;//若该节点没有赋值，说明出现了越节点赋值现象，报错
  68.         ans.push_back(u->v);//存入节点权值，按照从上到下从左到右
  69.         if(u->left!=NULL)q.push(u->left);//左
  70.         if(u->right!=NULL)q.push(u->right);//右--->循环递归！！借助queue
  71.     }
  72.     return true;
  73. }
  74. int main()
  75. {
  76.     while(1)
  77.     {
  78.         if(!read_in())//输入数据并且建树完成
  79.             break;
  80.         vector<int> ans;//ans用来存储权值，最后输出
  81.         if(!failed&&bfs(ans))//均无错误，则可输出
  82.         {
  83.             int l=ans.size();
  84.             for(int j=0;j<l;j++)//输出
  85.             {
  86.                 if(j==0)
  87.                     cout<<ans[j];
  88.                 else
  89.                     cout<<" "<<ans[j];
  90.             }
  91.             cout<<endl;
  92.         }
  93.         else
  94.             cout<<"not complete"<<endl;
  95.     }
  96.     return 0;
  97. }

 

<2>第二类数组实现

核心代码：

  1. void newtree()                        //初始化一颗新树，由于静态实现无法回收内存，因此顺便充当析构函数  
  2. {  
  3.     lch[root] = rch[root] = 0;  
  4.     have_value[root] = 0;  
  5.     cnt = root;  
  6. }  
  7. int newnode()                       //建立新节点的函数，其中0相当于结构体中的空指针  
  8. {  
  9.     int u = ++cnt;  
  10.     lch[u] = rch[u] = 0;  
  11.     have_value[u] = 0;  
  12.     return u;  
  13. }  
  14. void addnode(int v , char * s)      //建立新节点的过程  
  15. {  
  16.     int n = strlen(s);  
  17.     int u = root;  
  18.     for(int i = 0; i<n;i++){  
  19.         if(s[i] == 'L' ) {  //重点！
  20.             if(lch[u] == 0)  
  21.                 lch[u] = newnode();  
  22.             u = lch[u];  
  23.         }  
  24.         else if(s[i] == 'R'){  
  25.             if(rch[u] == 0)  
  26.                 rch[u] = newnode();  
  27.             u = rch[u];  
  28.         }  
  29.     }  
  30.     if(have_value[u])failed = true;  
  31.     value[u] = v;  
  32.     have_value[ u ] = 1;
  33. }  

具体代码： 数组实现二叉树

 

 

三.二叉树的三种遍历方式

 

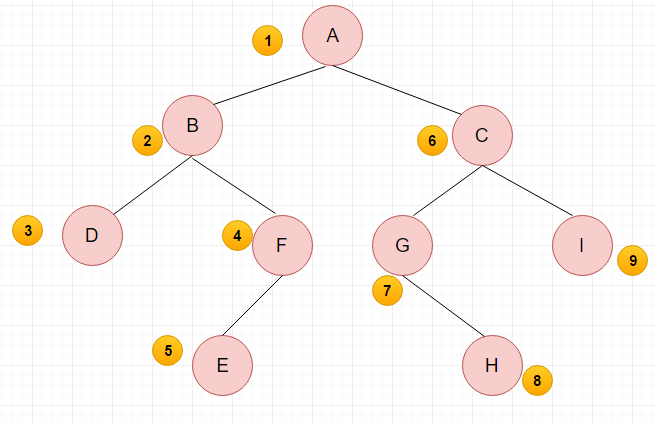
1.先序遍历：按照根节点->左子树->右子树的顺序访问二叉树

 

 

先序遍历：（1）访问根节点；（2）采用先序递归遍历左子树；（3）采用先序递归遍历右子树；

(注：每个节点的分支都遵循上述的访问顺序，体现“递归调用”)

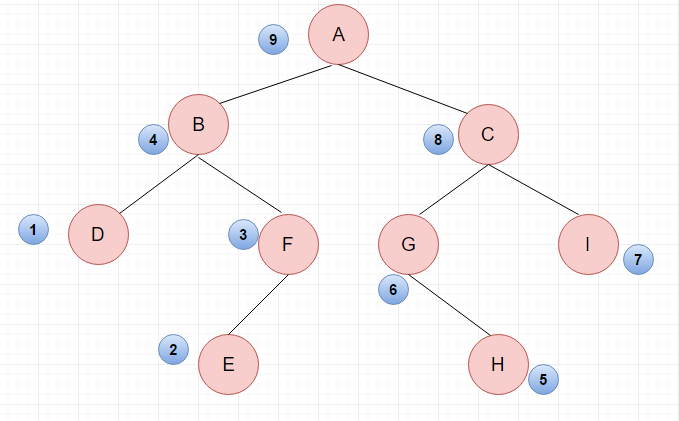
先序遍历结果：A BDFE CGHI

思维过程：（1）先访问根节点A，

（2）A分为左右两个子树，因为是递归调用，所以左子树也遵循“先根节点-再左-再右”的顺序，所以访问B节点，

（3）然后访问D节点，

（4）访问F节点的时候有分支，同样遵循“先根节点-再左--再右”的顺序,

(5)访问E节点，此时左边的大的子树已经访问完毕，

(6)然后遵循最后访问右子树的顺序，访问右边大的子树，右边大子树同样先访问根节点C,

(7)访问左子树G,

(8)因为G的左子树没有，所以接下俩访问G的右子树H,

(9)最后访问C的右子树I

 

 

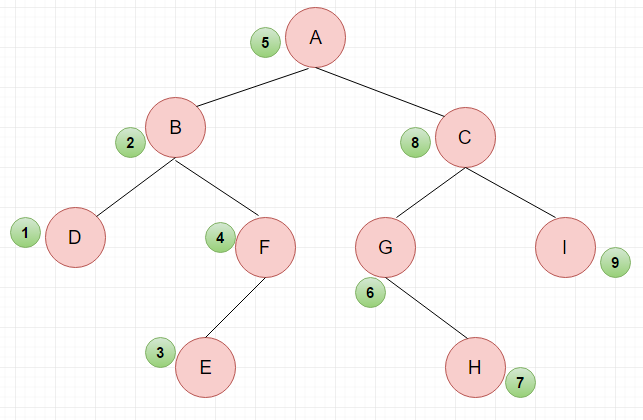
2.中序遍历：按照左子树->根节点->右子树的顺序访问

中序遍历：（1）采用中序遍历左子树；（2）访问根节点；（3）采用中序遍历右子树

 

中序遍历结果：DBEF    A    GHCI

 

3.后序遍历：按照左子树->右子树-->根节点的顺序访问

 

 

后序遍历：（1）采用后序递归遍历左子树；（2）采用后序递归遍历右子树；（3）访问根节点；

后序遍历的结果：DEFB  HGIC   A

 

小结：三种方法遍历过程中经过节点的路线一样；只是访问各个节点的时机不同，递归算法主要使用堆栈来实现。

 

4.例题1：uva548 树

（1）题意：输入一个二叉树的中序和后序，输出一个叶子节点，使得该叶子节点到根的数值总和最小。

Sample Input
3 2 1 4 5 7 6
3 1 2 5 6 7 4
7 8 11 3 5 16 12 18
8 3 11 7 16 18 12 5
255
255
Sample Output
1
3
255

（2）思路：

首先，我们先明确一个知识点，就是你知道了一棵树的中序和后序遍历，求他的前序遍历，我们应该怎么来做？

第一步：最初的时候，我们的后序遍历的最后一个数字就是我们的一个子树的根节点

第二步：找到我们的根结点后，跟据我们中序遍历的性质，我们的树就会被自然地分成了左右两个部分。

第三步：统计出来左右两个子树的大小和长度，这样就能继续重复上面的步骤

通过中序和后序来建树，然后递归找到所有节点到根节点的路径和，不断更新，最后输出即可！

 

（3）代码：

  1. #include <iostream>
  2. #include<string>
  3. #include<sstream>
  4. #include<algorithm>
  5. #include<cstdio>
  6. #include<cstring>
  7. using namespace std;
  8. const int maxn=10000+10;
  9. int lch[maxn],rch[maxn],in_order[maxn],post_roder[maxn];
  10. int n;
  11. int read_list(int* a)
  12. {
  13. //    memset(lch,0,sizeof(lch));
  14. //    memset(rch,0,sizeof(rch));
  15. //    memset(in_order,0,sizeof(in_order));
  16. //    memset(post_roder,0,sizeof(post_roder));
  17.     string line;
  18.     if(!getline(cin,line))return false;//因为题目说一行数据，没有结束标志，所以以回车为结束用字符串读入！
  19.     stringstream ss(line);
  20.     n=0;
  21.     int x;
  22.     while(ss>>x)a[n++]=x;//存入数组
  23.     return n>0;
  24. }
  25. int build(int L1,int R1,int L2,int R2)//建树各树的： 中序-后序
  26. {
  27.     if(L1>R1)return 0;//空树
  28.     int root=post_roder[R2];//树根是后序的最后一个字符
  29.     int p=L1;
  30.     while(in_order[p]!=root)p++;//在中序里找到左子树结点个数
  31.     int cnt=p-L1;//左子树个数
  32.     lch[root]=build(L1,p-1,L2,L2+cnt-1);//以root为根的左子树建树l1-p-1是中序的左边也就是左子树的中序，l2-l2+cnt-1是左子树的后序，看上面图片就可以知道，下面同，这样不断递归找到各个节点！
  33.     rch[root]=build(p+1,R1,L2+cnt,R2-1);//右子树建树
  34.     return root;
  35. }
  36. int best,best_sum;//最优解
  37. void dfs(int u,int sum)//找最优解
  38. {
  39.     sum+=u;
  40.     if(!lch[u]&&!rch[u])//没有左右子树了说明已经到达最低端叶子，该路径完成，判断是否最优解
  41.     {
  42.         if(sum<best_sum||(sum==best_sum&&u<best))
  43.         {
  44.             best_sum=sum;
  45.             best=u;
  46.         }
  47.     }
  48.     if(lch[u])dfs(lch[u],sum);//否则还在树枝上，继续向下找叶子
  49.     if(rch[u])dfs(rch[u],sum);
  50. }
  51. int main()
  52. {
  53.     while(read_list(in_order))//把中序读入数组in_order
  54.     {
  55.         read_list(post_roder);//读入后序post_order
  56.         build(0,n-1,0,n-1);//建树
  57.         best_sum=1000000000;//最优解
  58.         dfs(post_roder[n-1],0);//递归寻找最优解
  59.         cout<<best<<endl;
  60.     }
  61.     return 0;
  62. }

 

5.例题2：uva839 天平 （二叉树的递归输入）

（1）题意：根据干杠平衡原理，判断题目所给出的数据组成的天平能否平衡。注意，此天平可能包含子天平。输入时，如果w为0，则表示包含子天平，子天平按照先左后右的方法输入，子天平只需要判断w1*d1==w2*d2是否正确即可。那么父天平又如何判断呢？ 公式一样，不同的是，父天平的两边的重量是子天平砝码总和。  

Sample Input
1
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

Sample Output
YES

注意：该题在于怎么输入，题目的输入是按照构建天平进行的，什么时候天平构建完什么时候一组输入结束，所以这就要求一边输入一边建树，递归输入!!

代码：

  1. #include <iostream>
  2. using namespace std;
  3. bool solve(int &w)
  4. {
  5.     int w1,d1,w2,d2;
  6.     cin>>w1>>d1>>w2>>d2;
  7.     bool b1=true,b2=true;
  8.     if(!w1)b1=solve(w1);//如果w1=0,则说明w1有子树，同时把w1带入递归求出w1也就是子树总重量
  9.     if(!w2)b2=solve(w2);//同上
  10.     w=w1+w2;//求总重量，其实如果只考虑最上层的天平，这步似乎没什么意义；但其实它的意义在于，在当前是递归到一个子天平的情况时，就要重新输入子天平所在处的左右天平，如果有了这句代码，参数 W1 或者 W2,最终就能变为子天平上的两个左右天平的总重量。如此,等到判断 D1 * W1 == D2 * W2时，W1 和 W2就都不会是0了，而是该子天平下所有子天平的总重量(如果有的话，没有子天平，就还是它本身的质量，总之不会是0，而是它自己或是自己所有子天平的重量
  11.     return b1&&b2&&(w1*d1==w2*d2);//要想平衡，每一个天平都要平衡！
  12. }
  13. int main()
  14. {
  15.     int T,W;
  16.     cin>>T;//组数
  17.     while(T--)
  18.     {
  19.         if(solve(W))//输入同时判断
  20.             cout<<"YES"<<endl;
  21.         else
  22.             cout<<"NO"<<endl;
  23.         if(T)
  24.             cout<<endl;
  25.     }
  26.     return 0;
  27. }

 

6.建树技巧

（1）如果题目给出了每一个节点的位置描述，则每个节点递归赋值即可，类似于例题二：

  1. void addnode(int v,char *a)//建树
  2. {
  3.     int len=strlen(a);
  4.     Node *u=root;
  5.     for(int i=0;i<len;i++)
  6.     {
  7.         if(a[i]=='L')//左
  8.         {
  9.             if(u->left==NULL)u->left=newnode();//若左节点没有分配内存，没有开辟过，则申请内存，因为经过该节点了，该节点必须赋值！
  10.             u=u->left;//更新路径
  11.         }
  12.         else if(a[i]=='R')//右
  13.         {
  14.             if(u->right==NULL)u->right=newnode();//同上
  15.             u=u->right;
  16.         }
  17.     }
  18. }

（2）但是如果题目给出的是整棵树的路径顺序，如整棵树的先序，后序等等，这时候就需要整棵树按照给予的字符串递归建树，类似uva297四分树的指针结构体建树思路：

  1. Node* createNode(char* s) { //递归建树 
  2.  
  3.     if (s[n]=='\0') return NULL; 
  4.  
  5.     Node* pNode=new Node; 
  6.  
  7.     if (s[n]=='p') { 
  8.         pNode->type=0; 
  9.  
  10.         n++; 
  11.  
  12.         pNode->fch=createNode(s); 
  13.  
  14.         pNode->sch=createNode(s); 
  15.  
  16.         pNode->tch=createNode(s); 
  17.  
  18.         pNode->lch=createNode(s); 
  19.     } 
  20.  
  21.     else if (s[n]=='f') { 
  22.         pNode->type=1; 
  23.  
  24.         n++; 
  25.     } 
  26.  
  27.     else { 
  28.         pNode->type=2; 
  29.  
  30.         n++; 
  31.     } 
  32.  
  33.     return pNode; 
  34.  
  35. } 

注意全局变量或者引用的使用来改变n的值最为关键！！

 

（3）练习：

<1>已知二叉树的一个按先序遍历输入的字符序列，如abc,,de,g,,f,,, (其中,表示空结点)。请建立二叉树并按中序和后序的方式遍历该二叉树。

注：若题目给出空节点，则只需一个先序字符串就可以建树，然后递归求得中序后序，若求层次遍历，则要用队列！若不给出空节点，则只能用两个序列字符串才能建树！

 

代码：

  1. #include <iostream>
  2. #include<queue>
  3. #include<cstdio>
  4. #include<vector>
  5. using namespace std;
  6. struct Node
  7. {
  8.     char ch;
  9.     Node *lefted,*righted;
  10.     Node():ch(0),lefted(NULL),righted(NULL) {}
  11. };
  12. Node *newnode()
  13. {
  14.     return new Node();
  15. };
  16. Node *Root;
  17. Node *build(const char *s,int& p)
  18. {
  19.  
  20.     char sign=s[p++];
  21.     if(sign==',')
  22.         return NULL;
  23.     else
  24.     {
  25.         Node *root;
  26.         root=newnode();
  27.         root->ch=sign;
  28.         root->lefted=build(s,p);
  29.         root->righted=build(s,p);
  30.         return root;
  31.     }
  32.  
  33. }
  34. void solveZ(Node *tree)
  35. {
  36.     if(tree)
  37.     {
  38.         solveZ(tree->lefted);
  39.         cout<<tree->ch;
  40.         solveZ(tree->righted);
  41.     }
  42. }
  43. void solveH(Node *tree)
  44. {
  45.     if(tree)
  46.     {
  47.         solveH(tree->lefted);
  48.         solveH(tree->righted);
  49.         cout<<tree->ch;
  50.     }
  51. }
  52. int main()
  53. {
  54.     char name[100];
  55.     while(scanf("%s",name)!=EOF)
  56.     {
  57.         int m=0;
  58.         Root=build(name,m);
  59.         solveZ(Root);
  60.         cout<<endl;
  61.         solveH(Root);
  62.         cout<<endl;
  63.     }
  64.     return 0;
  65. }

 

<2>输入二叉树的先序遍历序列和中序遍历序列，输出该二叉树的后序遍历序列。

第一行输入二叉树的先序遍历序列；
第二行输入二叉树的中序遍历序列。

输出该二叉树的后序遍历序列。

ABDCEF

BDAECF

 

DBEFCA

代码：

  1. #include <iostream>
  2. #include<cstdio>
  3. #include<cstring>
  4. using namespace std;
  5. char pre_name[100];
  6. char in_name[100];
  7. struct Node
  8. {
  9.     char ch;
  10.     Node *lefted,*righted;
  11.     Node():ch(0),lefted(NULL),righted(NULL) {}
  12. };
  13. Node *Root;
  14. Node *build(int L1,int R1,int L2,int R2)//前序找根，中序分割建树
  15. {
  16.     if(L2>R2)return NULL;
  17.     Node *root;
  18.     root=new Node();
  19.     root->ch=pre_name[L1];
  20.     int p=L2;
  21.     while(in_name[p]!=root->ch)p++;
  22.     int cnt=p-L2;
  23.     root->lefted=build(L1+1,L1+cnt,L2,p-1);
  24.     root->righted=build(L1+cnt+1,R1,p+1,R2);
  25.     return root;
  26. }
  27. void select_post(Node *tree)
  28. {
  29.     if(tree)
  30.     {
  31.         select_post(tree->lefted);
  32.         select_post(tree->righted);
  33.         cout<<tree->ch;
  34.     }
  35. }
  36. int main()
  37. {
  38.     scanf("%s%s",pre_name,in_name);
  39.     int n=strlen(pre_name);
  40.     Root=build(0,n-1,0,n-1);
  41.     select_post(Root);
  42.     cout<<endl;
  43.     return 0;
  44. }

 

<3>已知一个按先序输入的字符序列，如abd,,eg,,,cf,,,(其中,表示空结点)。请建立二叉树并求二叉树的层次遍历序列。

输入数据有多行，第一行是一个整数t (t<1000)，代表有t行测试数据。每行是一个长度小于50个字符的字符串。

 输出二叉树的层次遍历序列。

2
abd,,eg,,,cf,,,
xnl,,i,,u,,

abcdefg
xnuli

代码：

  1. #include <iostream>
  2. #include<cstdio>
  3. #include<cstring>
  4. #include<queue>
  5. #include<vector>
  6. using namespace std;
  7. char pre_name[100];//如果给出空节点的，则一个序列遍历就可建树，否则要两个序列！且层次遍历用队列，其他遍历用递归即可！
  8. struct Node
  9. {
  10.     char ch;
  11.     Node *lefted,*righted;
  12.     Node():ch(0),lefted(NULL),righted(NULL) {}
  13. };
  14. Node *Root;
  15. Node *build(const char *s,int &p)
  16. {
  17.     char sign=s[p++];
  18.     if(sign==',')
  19.         return NULL;
  20.     else
  21.     {
  22.         Node *root;
  23.         root=new Node();
  24.         root->ch=sign;
  25.         root->lefted=build(s,p);
  26.         root->righted=build(s,p);
  27.         return root;
  28.     }
  29. }
  30. void serch(vector<char>&u)
  31. {
  32.     queue<Node*>que;
  33.     u.clear();
  34.     if(Root)//要考虑根节点为空的情况！！！！
  35.     {
  36.         que.push(Root);
  37.     }
  38.     while(!que.empty())//队列递归求层序遍历！！
  39.     {
  40.         Node *nodes=que.front();
  41.         que.pop();
  42.         u.push_back(nodes->ch);
  43.         if(nodes->lefted!=NULL)que.push(nodes->lefted);
  44.         if(nodes->righted!=NULL)que.push(nodes->righted);
  45.     }
  46. }
  47. int main()
  48. {
  49.     int T;
  50.     cin>>T;
  51.     getchar();
  52.     while(T--)
  53.     {
  54.         scanf("%s",pre_name);
  55.         int m=0;
  56.         Root=build(pre_name,m);
  57.         vector<char>ans;
  58.         serch(ans);
  59.         for(int i=0; i<ans.size(); i++)
  60.             cout<<ans[i];
  61.         cout<<endl;
  62.     }
  63.     return 0;
  64. }

 

 四.二叉树的层序遍历以及求宽度

1.二叉树的层序遍历

（1）什么是层序遍历？

就是按照二叉树的层次高低遍历，优先遍历第一层的所有节点，然后遍历第二层，以此类推。

层序遍历结果： F CE ADHG BM

（2）实现（非递归队列）

利用队列先入先出特点，放入顺序正好按照层序从上至下。

代码：c语言

  1. void LevelorderTraversal( BinTree BT ){
  2.    int head = 0;
  3.    int last = 0;
  4.    if(BT==NULL)return;
  5.    BinTree NodeList[1000];
  6.    NodeList[last++] = BT;
  7.    while(head<last){
  8.         BinTree node = NodeList[head++];
  9.         printf(" %c",node->Data);
  10.         if(node->Left)
  11.              NodeList[last++] = node->Left;
  12.         if(node->Right)
  13.              NodeList[last++] = node->Right;
  14.    }
  15. }

c++队列：

  1. void LevelorderTraversal( BinTree BT ){//²ãÐò±ãÀû
  2.     queue<BinTree> que;
  3.     que.push(BT);
  4.     while(!que.empty()){
  5.         BinTree T = que.front();
  6.         que.pop();
  7.         printf(" %c",T->Data);
  8.         if(!T->Left)que.push(T->Left);
  9.         if(!T->Right)que.push(T->Right);
  10.     }
  11. }

2.二叉树求宽度

（1）什么是二叉树的宽度？

二叉树的宽度是二叉树每一层中的最大节点个数。

（2）分析：

根据二叉树求层序遍历的特点，这里仍用队列实现

<1>法1：每个节点记录自己所在层数，用数组记录每个层数的节点数，取最值即可。

  1. int getWidth(BTree T){
  2.     memset(sum,0,sizeof(sum));
  3.     queue<BTree> que;
  4.     T->Rank = 1;
  5.     que.push(T);
  6.     int MaxWid = 0;
  7.     while(!que.empty()){
  8.         BTree t = que.front();
  9.         que.pop();
  10.         sum[t->Rank]++;
  11.         MaxWid = max(MaxWid,sum[t->Rank]);
  12.         if(t->lefted!=NULL){
  13.             t->lefted->Rank = t->Rank+1;
  14.             que.push(t->lefted);
  15.         }
  16.         if(t->righted!=NULL){
  17.             t->righted->Rank = t->Rank + 1;
  18.             que.push(t->righted);
  19.         }
  20.     }
  21.     return MaxWid;
  22. }

<2>法二：队列里面只存储当前层节点，队列长度就是当前层节点数目。

  1. int GetWidth(BTree T){
  2.     queue<BTree> que;
  3.     que.push(T);
  4.     int MaxWid = 0;
  5.     while(1){
  6.         int len = que.size();
  7.         MaxWid = max(MaxWid,len);
  8.         if(len==0)break;
  9.         while(len > 0){
  10.             BTree t = que.front();
  11.             que.pop();
  12.             len--;
  13.             if(t->lefted!=NULL)que.push(t->lefted);
  14.             if(t->righted!=NULL)que.push(t->righted);
  15.         }
  16.     }
  17.     return MaxWid;
  18. }

 

posted on 2022-07-20 23:07  DoubleLi  阅读(413)  评论(0)    收藏  举报