[洛谷][noip][算法竞赛进阶指南]小猫爬山 原创

题目来源 洛谷

算法标签 DFS

题目简介

思路

这道题比较好玩

我们要放猫，要自己开新的车

第一步在查找的时候，事实上你时没有车的
这个时候你只能考虑开一辆新车来放🐱

而第二次抱猫，这个时候你就需要思考了，我们唯一拥有的车子是否有剩余的空间？
我们是该放入车里，还是新开一个车来?

每次抱一只新的猫的时候，你都需要从0到当前所有车辆的车子中考虑一遍

以下是 u为当前选择的猫 来考虑摆放在哪一个车上的思路

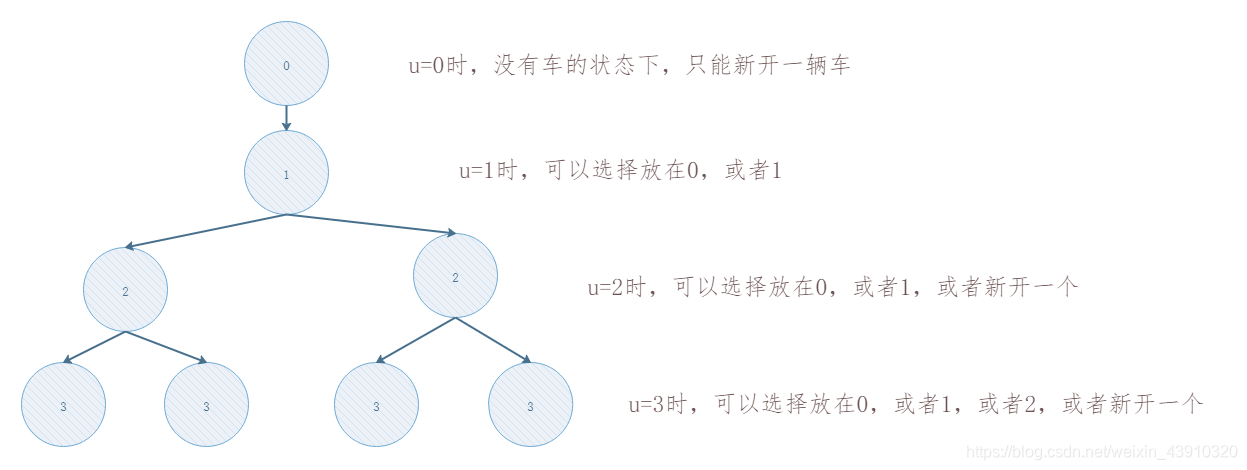
我们来优化整个过程

这是整个优化的思路

那么，我们可以直接使用贪心吗？
我编写了一个简单的贪心的思路，检查车有没有空余，如果当前的猫能放我就放入，不能的话就开新车

#include<iostream>
#include<algorithm>

using namespace std;

const int N=1e5+10;
int n,w;
int a[N],sum[N];
int cnt;

bool check(int weight)//检查猫能不能放入车内
{
    for(int i=1;i<=cnt;i++)
        if(weight+sum[i]<=w){sum[i]+=weight;return true;}//能放入，退出
    
    return false;
}

int main()
{
    cin>>n>>w;//n 数量 w 每辆车的最大容量
    
    for(int i=0;i<n;i++)cin>>a[i];//读入数据
    
    sort(a,a+n,[](int a,int b){return a>b;});//反序排序
    
    sum[++cnt]=a[0];//初始化第一辆车
    
    for(int i=1;i<n;i++)if(!check(a[i]))sum[++cnt]=a[i];//如果容量不够放入，我们就需要初始化一辆新的车
    
    for(int i=1;i<n;i++)cout<<sum[i]<<" ";//写出每辆车的现存载重
    
    cout<<endl;
    
    cout<<cnt;//输出车的数量
    
    return 0;
}

数据读出

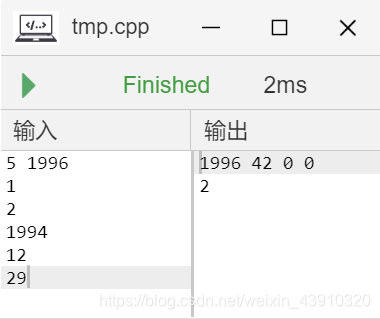
我们过掉了样例，那我们成功了吗？
没有
在maxV=16时，重量为9 5 5 5 4 3 的情况下进行测试
贪心结果是9+5 5+5+4 3，结果为3 与我代码的逻辑吻合
但正确结果为9+4+3 5+5+5，结果为2 实际的数量却实际更小
因此我们不能直接盲目使用贪心

在实际的数据当中我们也遇到了相同的问题

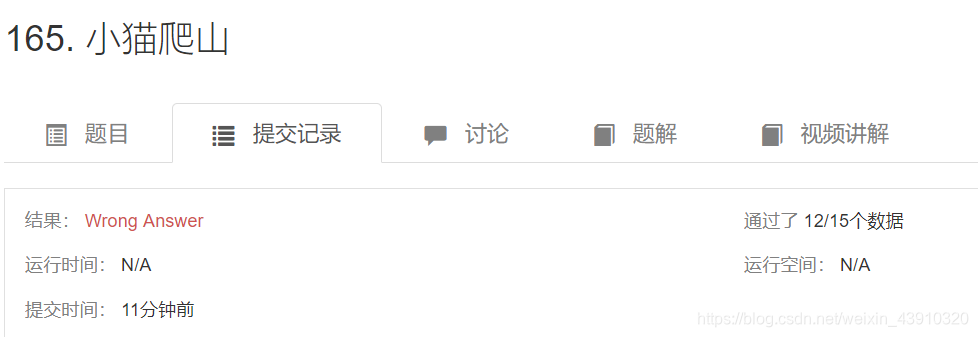
于是我们可以发现，贪心的逻辑在这里是不可行的
我们可以使用DFS暴力搜索每一种方案,即🐱可以放置在现有的🚗中的任意一辆车上,例如

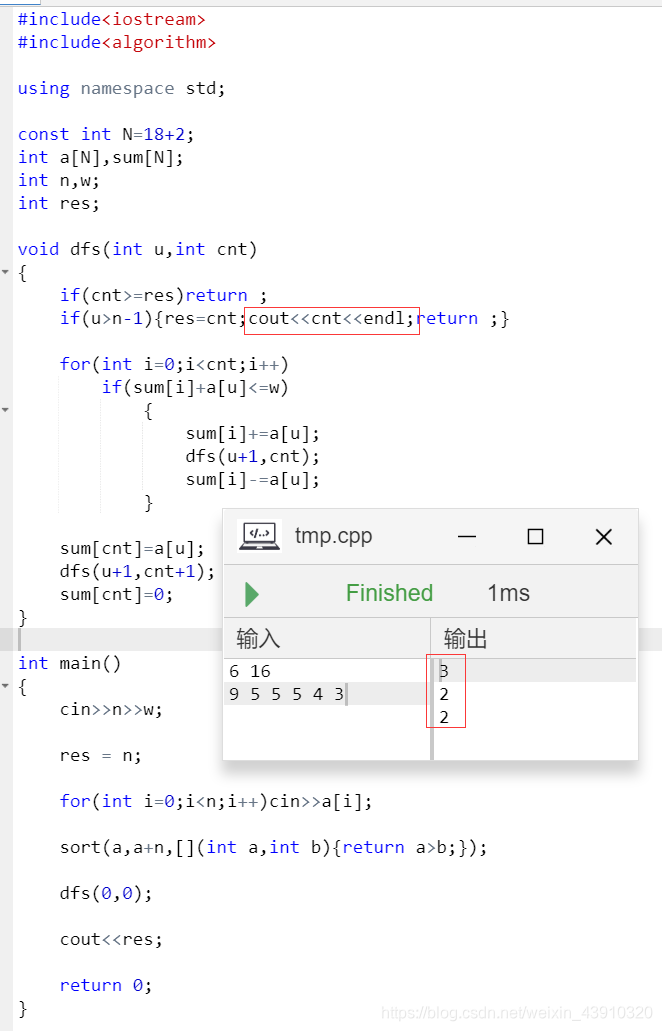
这里我们输出了所有方案的数量，我们会发现在我们的贪心方法错误的数据当中，我们更新到了最优的答案

那么，为什么数据会逐渐变小呢?

	if(cnt>=res)return ;
    if(u>n-1){res=cnt;return ;}
在这两行代码中
	第二行代码，我们选择完了之后进行更新答案
	第一行代码，我们检查当前答案是否大于历史最优值，如果大于，就不继续检查，而是直接返回

AC代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N=18+2;
int a[N],sum[N];//a 小猫重量 sum 车现载重
int n,w;
int res;

void dfs(int u,int cnt)//u 当前第几只猫，cnt当前车的数量
{
    if(cnt>=res)return ;//如果车的数量大于现实存在的猫咪的个数，或者历史最优的数值，返回
    if(u>n-1){res=cnt;return ;}//如果考虑完了n只即所有猫咪，则更新答案
    
    for(int i=0;i<cnt;i++)
        if(sum[i]+a[u]<=w)//检查现有的所有车的重量，是否能放猫
            {
                sum[i]+=a[u];
                dfs(u+1,cnt);
                sum[i]-=a[u];
            }
    
    sum[cnt]=a[u];//新增一辆车，初始重量是当前猫的重量
    dfs(u+1,cnt+1);
    sum[cnt]=0;
}

int main()
{
    cin>>n>>w;
    
    res = n;
    
    for(int i=0;i<n;i++)cin>>a[i];
    
    sort(a,a+n,[](int a,int b){return a>b;});//反序排序 优化了搜索顺序 lambda表达式

    dfs(0,0);

    cout<<res;
    
    return 0;
}

反序排序优化，优化了就是20MS，如果未优化则是90MS

具体数值