[图论]Prim算法求最小生成树 原创

算法标签 prim

题目来源

题目简介

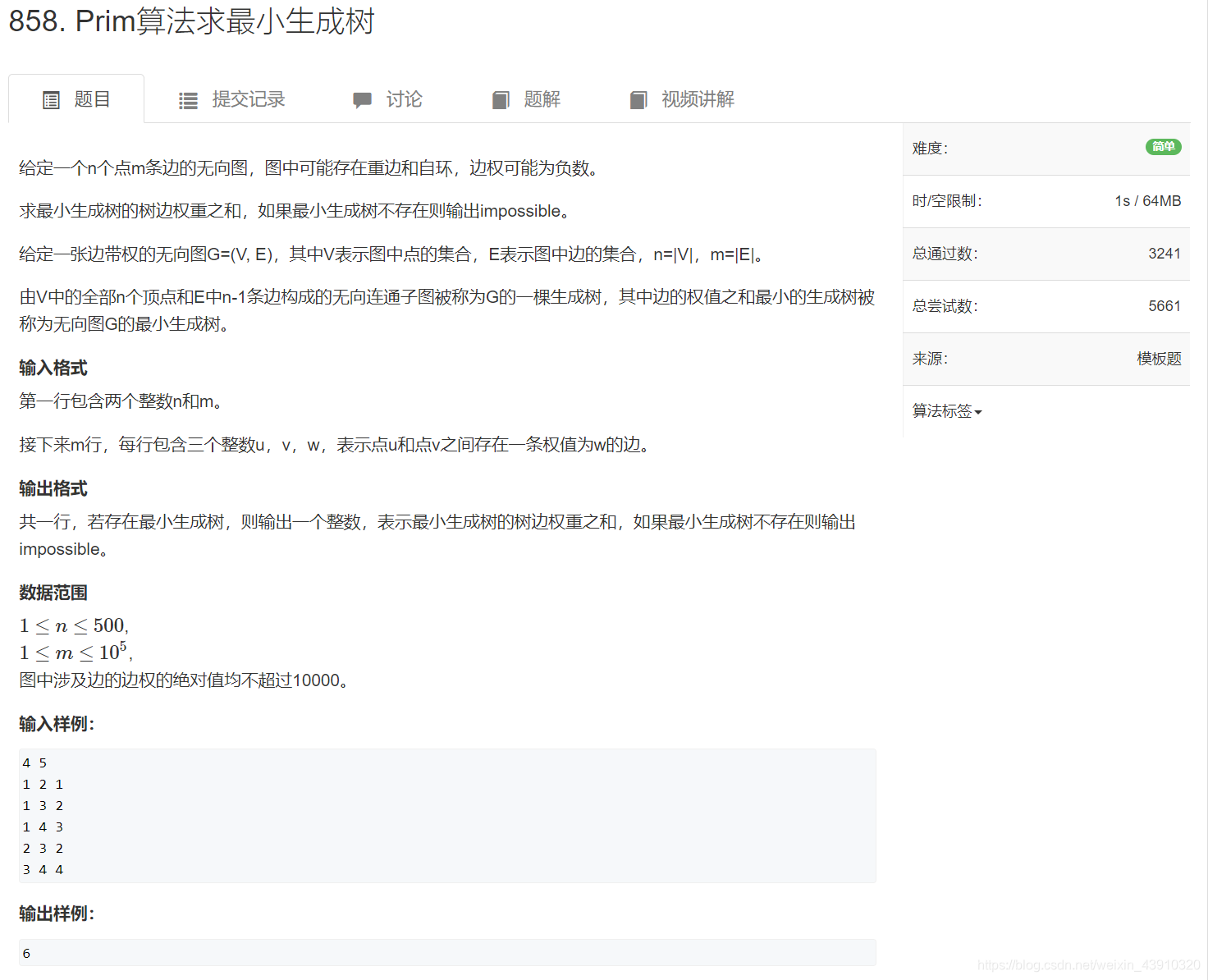
思路

prim

1.把所有距离初始化为正无穷
2.找到集合外距离最近的点t，集合 指的是 在联通块中的点
3.用t来更新其他点到集合的最短距离
4.把t加到集合中去

1.初始化 正无穷

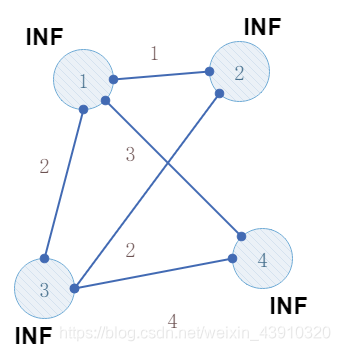
2.因为集合没有任何点，我们随便找一个点接入集合

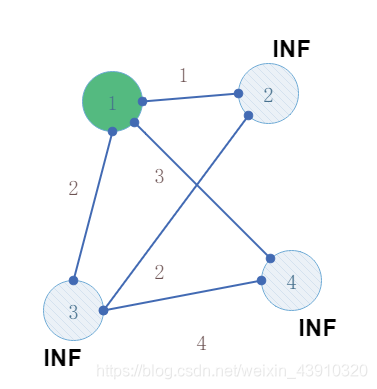
3.用t 更新其他点到集合的距离
即 其他点到t的距离，否则就继续是INF

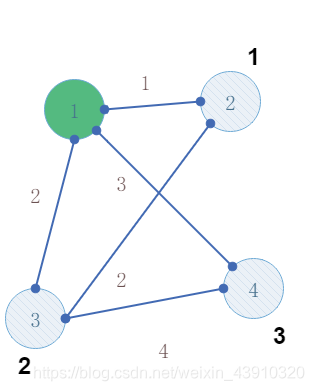
4.t 放入集合 我们已经使其变绿 放入

第二次迭代
2.选中剩下距离到集合最近的点
3.用t 更新其他点到集合的距离
但这里，我们的各个点的最近距离更新之后也并没发生变化
4.t 放入集合 我们已经使其变绿 放入

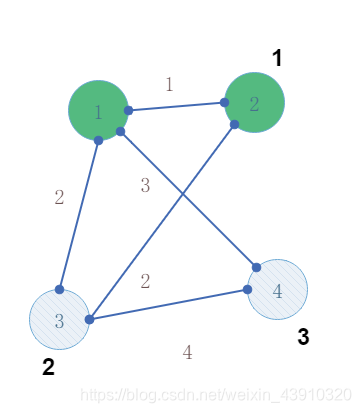
第三次迭代
这里更新比较之后也没有产生变化

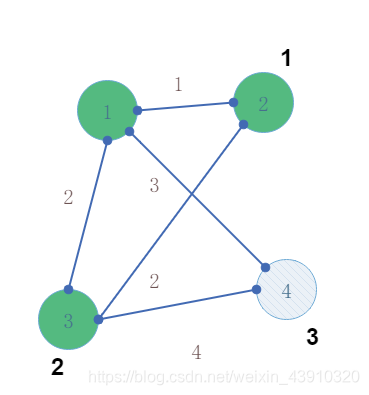
第四次迭代

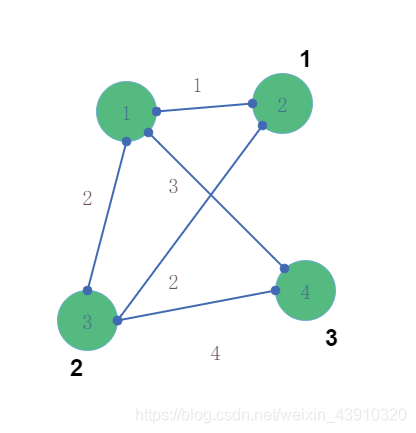
最小生成树是什么意思呢？
可以理解为我们每一次把新的点接入集合的过程中，存在的对于集合的边的最短的那一个

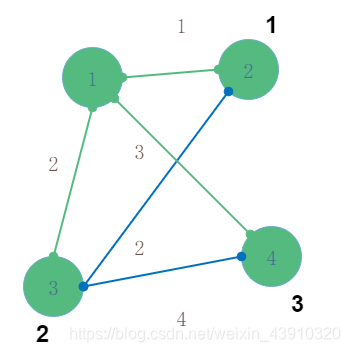
如图
点1到点2 距离为1的边
点3到点1 或者 点2 距离为2的边 （因为有两个边可以选择，我们取最小）
点4到点1 距离为3的边

AC代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N=500+10;//N的点的数量
const int INF = 0x3f3f3f3f;//设置一个初始最大值

int g[N][N];//一个稠密图 g[i][j] 从i到j的距离
int dist[N];//用来存储各个点距离集合的距离
bool st[N];//用来判断各个点是否在集合之内

int n,m;

int prim()//prim算法
{
    int sum=0;
    for(int i=0;i<n;i++)//n次迭代
        {
            int t=-1;//标记为一次迭代中，所有剩余的在集合外的点中距离集合最近的距离
            for(int j=1;j<=n;j++)//寻找剩余的点中 距离离集合最近的点
                if(!st[j]&&(t==-1||dist[t]>dist[j]))t=j;//如果这个点在集合外 且 是第一个或者距离比当此寻找的t更小 那么就把t更新
            
            if(i&&dist[t]==INF)return INF;//如果不是第一次迭代，那么说明dist t 起码应该是有值对的，如果最小值都是INF，说明不连通
            
            if(i)sum+=dist[t];//如果不是第一次迭代，最小生成树添加该边的距离
            
            st[t]=true;//当前这个点 t(剩余的点中距离集合最短的点) 被纳入集合
            
            for(int i=1;i<=n;i++)dist[i]=min(dist[i],g[t][i]);//使用t来更新其他点到集合的距离
			//t是 当次遍历中（也就是剩下未进入集合的点中）距离集合距离最短的 新的 点
        }
    return sum;//返回最小生成树的总长
}
int main()
{
    memset(g,0x3f,sizeof g);
    memset(dist,0x3f,sizeof dist);//给两个图赋无穷大
    
    cin>>n>>m;
    
    int u,v,w;
    while(m--)
    {
        cin>>u>>v>>w;
        g[u][v]=g[v][u]=min(g[u][v],w);//无向图的特征 从u到u 从u到v 都是一个距离，且有可能重边，所有取自身和W最小
    }
    
    int res = prim();
    if(res==INF)cout<<"impossible";else cout<<res;
    return 0;
}