[洛谷]P1048 采药原创

算法标签 01背包问题

题目简叙

我们先进行盲目的贪心方式

这里我们直接计算单价最高，然后按照单价降序排序，每次都获得单价最高

#include<iostream>
#include<vector>
#include<algorithm>

#define x first 
#define y second

using namespace std;
const int N=1e3+10;

typedef pair<int,int> PII;
vector<PII> arr;

int main()
{
    int t,m;
    cin>>t>>m;
    
    int tx,ty;
    for(int i=1;i<=m;i++){cin>>tx>>ty;arr.push_back({tx,ty});}
    
    sort(arr.begin(),arr.end(),[](PII a,PII b){return a.y/a.x>b.y/b.x;});//相当于结构体排序，排序规则是按照单价最高从大到小
    
    int res=0;我们先进行盲目的贪心方式

这里我们直接计算单价最高，然后按照单价降序排序，每次都获得单价最高
```cpp
#include<iostream>
#include<vector>
#include<algorithm>

#define x first 
#define y second

using namespace std;
const int N=1e3+10;

typedef pair<int,int> PII;
vector<PII> arr;

int main()
{
    int t,m;
    cin>>t>>m;
    
    int tx,ty;
    for(int i=1;i<=m;i++){cin>>tx>>ty;arr.push_back({tx,ty});}
    
    sort(arr.begin(),arr.end(),[](PII a,PII b){return a.y/a.x>b.y/b.x;});//相当于结构体排序，排序规则是按照单价最高从大到小
    
    int res=0;
    for(PII N:arr)if(t>=N.x)res+=N.y,t-=N.x;
    
    cout<<res;
    
    return 0;
}

检测数据

这里我们看起来是对了，但究其根本，我们完全不清除这样的贪心是否是正确的决策

继续通过更多的数据

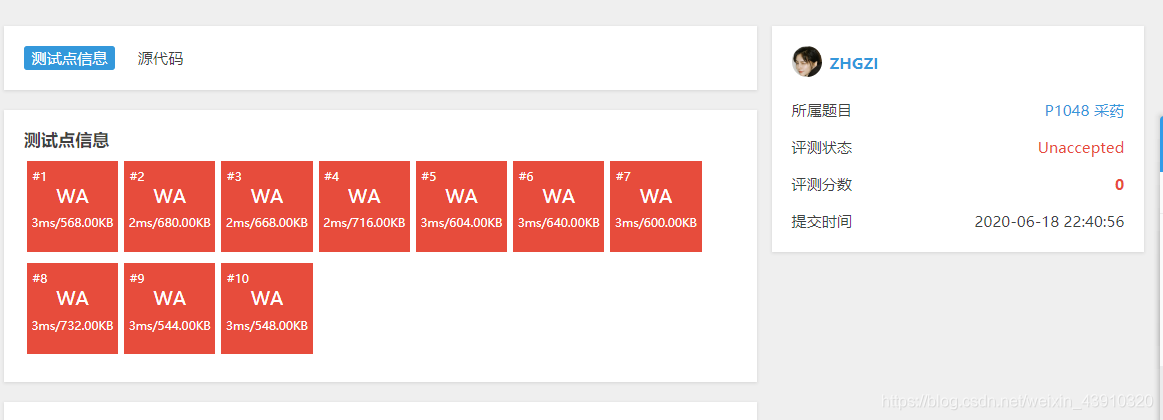
我们会发现，所有的测试点都出问题了，可见我们的策略是有错误的

我们进行第二种方法

从N个物品里面选择K个物品，并且有着条件限制且只能拿一次，是非常明显的01背包问题
我们复习一次，01背包问题的思考方式
即：
1.正常存储我们所需要读入的数据
2.确定我们的状态表示
3.确定我们的限制条件
4.确定我们的状态转移方程
5.输出答案

以这道题为例，我们首先开始明确参数：

1.T     则表明我们一共有T的时间
2.M     这表明我们一共有M的草药
3.TIME  这表明我们每颗草药分别需要消耗TIME[i] 的时间
4.VALUE 这表明我们每颗草药分别可以获得VALUE[i]的价值

我们思考每个可能存在的状态时，可以表达为
arr[i][j] 即该状态表明，
参数i->现在我们开始判定第i个草药是否需要摘取
参数j->现在我们一共还剩下j的时间可以采药
f[i][j]->表明这个状态下我们一共有 f[i][j]的价值

集合
所以我们相当于一直在考虑不同时间长度不同选择草药的方案的集合（考虑了前i个物品重量为j 的方案的集合）

状态转移方程
我们每次摘取，都要考虑摘取这一次是否能使得我们获得的价值更高
即我们是否该选择第i个

获取答案
我们可以检查在不同背包的容量情况下，我们的价值最高的是哪一个

以下是我们整个的逻辑过程

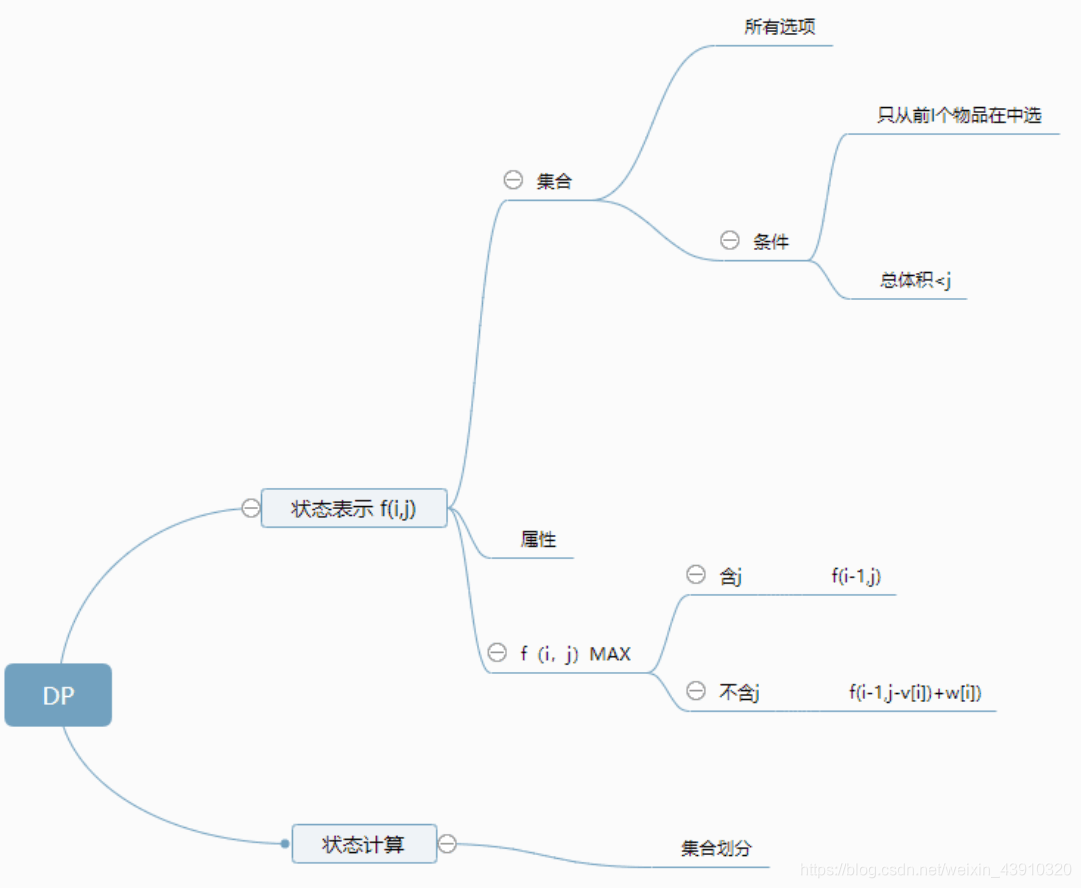
#include<iostream>

using namespace std;
const int N=1e3+10;
int arr[N][N*10];
int Time[N],value[N];

int main()
{
    int t,m;
    cin>>t>>m;
    
    for(int i=1;i<=m;i++)cin>>Time[i]>>value[i];//读取数据
    
    for(int i=1;i<=m;i++)    //状态表示
        for(int j=1;j<=t;j++)
            if(j>=Time[i])arr[i][j]=max(arr[i-1][j],arr[i-1][j-Time[i]]+value[i]);//如果剩余有时间，我们就摘取
            else arr[i][j]=arr[i-1][j];//否则就不摘
    
    int res=-1;    
    for(int i=1;i<=t;i++)res=max(res,arr[m][i]);//找到不同剩余时间下的最大价值
    cout<<res;
    
    return 0;
}

空间优化

#include<iostream>

using namespace std;
const int N=1e3+10;
int arr[N*10];
int Time[N],value[N];

int main()
{
    int t,m;
    cin>>t>>m;
    
    for(int i=1;i<=m;i++)cin>>Time[i]>>value[i];
    
    for(int i=1;i<=m;i++)    
        for(int j=t;j>=Time[i];j--)
            arr[j]=max(arr[j],arr[j-Time[i]]+value[i]);//我们可以依照上面的逻辑直接把二维优化成一维
    
    cout<<arr[t];//因为优化成了一维，所有数据只有不变和变大，我们直接输出最终值即可
    
    return 0;
}

第二次优化空间

#include<iostream>

using namespace std;
const int N=1e4+10;
int arr[N];

int main()
{
    int t,m;
    cin>>t>>m;
    
    int Time,value;
    for(int i=1;i<=m;i++)
    {
        cin>>Time>>value;
        for(int j=t;j>=Time;j--)
            arr[j]=max(arr[j],arr[j-Time]+value);//直接把F降维成一维，Time,Value省去存储空间
    }

    cout<<arr[t];
    
    return 0;
}

我们这个时候可以发现的问题在于
DP的概念和记忆化搜索很相似

for(PII N:arr)if(t>=N.x)res+=N.y,t-=N.x;

cout<<res;

return 0;

}