【算法4】5.5.6.哈夫曼编码

数据压缩算法

霍夫曼编码

霍夫曼编码（Huffman Coding)

霍夫曼编码是一种能够大幅压缩自然语言文件空间的数据压缩技术。

主要思想：用较少的比特表示出现频率高的字符，用较多的比特表示出现频率低的字符。

变长前缀码

前缀码：如果所有字符编码都不会成为其他字符编码的前缀，那么就不需要分隔符了。含有这种性能的编码规则叫做前缀码。（像 7 位 ASCII 编码这样的定长编码也是前缀码）

前缀码的单词查找树

用单词查找树表示前缀码：任意含有 M 个空链接的单词查找树都为 M 个字符定义了一种前缀码方法：将空链接替换成指向叶子结点的链接，每个叶子结点都含有一个需要编码的字符。每个字符的编码就是从根结点到该结点的路径表示的比特字符串（只含有 0 和 1 的字符串，即编码的二进制的字符串表示），其中左链接表示 0，右链接表示 1。

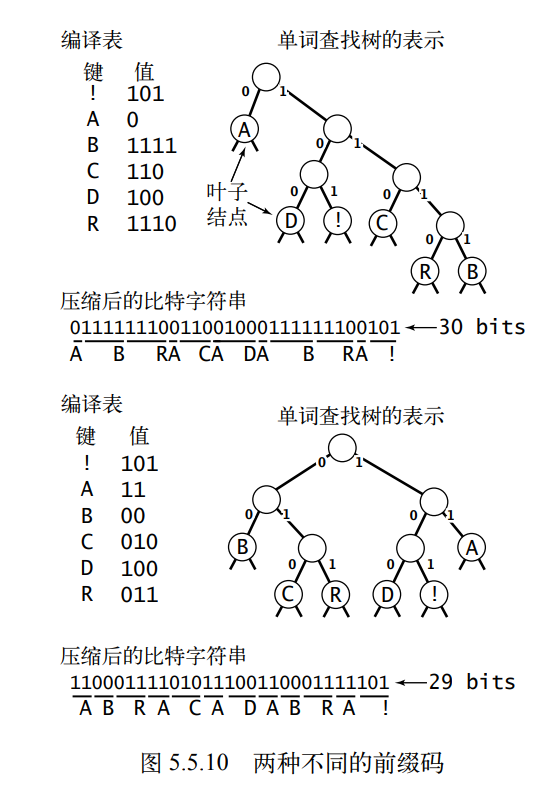
霍夫曼编码是一种能够为任意字符串构造一棵能够将比特流最小化的单词查找树的算法。（即压缩率最高的前缀码表示）

霍夫曼编码实现

编码过程：

• 根据待编码的字符串构造最优单词查找树（需对每个字符出现的频率进行统计）
• 根据单词查找树构造编译表（字符到二进制编码的字符串表示的映射表）
• 将单词查找树写入输出流
• 将字符数量写入输出流
• 将编码结果写入输出流

解码过程：

• 从输入流读取单词查找树
• 从输入流读取字符数量
• 从输入流读取二进制位值并根据单词查找树解码出字符

// 前缀码单词查找树结点
@Data
public class Node implements Comparable<Node> {
    private char c; // 叶子结点保存的字符
    private int freq; // 字符出现的频率
    private Node left, right;

    public Node(char c, int freq, Node left, Node right) {
        this.c = c;
        this.freq = freq;
        this.left = left;
        this.right = right;
    }

    public boolean isLeaf() {
        return left == null && right == null;
    }


    // 用于优先队列
    @Override
    public int compareTo(Node that) {
        return this.freq - that.freq;
    }
}

// 霍夫曼编码
// 编码：compress()
// 解码：expand()
public class Huffman {
    private static final int R = 128; // ASCII 字符集大小
    private static final char INNER_NODE = '\0'; // 内部结点的字符
    private static final int EXPAND_FREQ = -1; // 解码时的结点频率

    // 编码
    public static void compress() {
        String s = BinaryStdIn.readString();
        int[] freq = statFreq(s);
        final Node root = buildTrie(freq);
        String[] table = buildCode(root);
        writeTrie(root);
        BinaryStdOut.write(s.length());
        for (int i = 0; i < s.length(); i++) {
            String code = table[s.charAt(i)];
            for (int j = 0; j < code.length(); j++) {
                if ("1".equals(code.charAt(j))) {
                    BinaryStdOut.write(true);
                } else {
                    BinaryStdOut.write(false);
                }
            }
        }
    }

    // 解码
    public static void expand() {
        final Node root = readTrie();
        int N = BinaryStdIn.readInt();
        for (int i = 0; i < N; i++) {
            Node node = root;
            while (!node.isLeaf()) {
                if (BinaryStdIn.readBoolean()) {
                    node = node.getRight();
                } else {
                    node = node.getLeft();
                }
            }
            BinaryStdOut.write(node.getC());
        }
        BinaryStdOut.close();
    }

    // 统计每个字符出现的频率
    private static int[] statFreq(String s) {
        int[] freq = new int[R];
        for (int i = 0; i < s.length(); i++) {
            freq[s.charAt(i)]++;
        }
        return freq;
    }

    // 根据频率构造单词查找树
    private static Node buildTrie(int[] freq) {
        PriorityQueue<Node> pq = new PriorityQueue<>();
        for (char c = 0; c < R; c++) {
            if (freq[c] > 0) {
                pq.add(new Node(c, freq[c], null, null));
            }
        }
        while (pq.size() > 1) {
            Node left = pq.remove();
            Node right = pq.remove();
            Node parent = new Node(INNER_NODE, left.getFreq() + right.getFreq(), left, right);
            pq.add(parent);
        }
        return pq.remove();
    }

    // 根据单词查找树构编译表
    // 即字符到二进制编码映射表
    private static String[] buildCode(Node root) {
        String[] table = new String[R];
        buildCode(root, table, "");
        return table;
    }

    private static void buildCode(Node node, String[] table, String code) {
        if (node.isLeaf()) {
            table[node.getC()] = code;
            return;
        }
        buildCode(node.getLeft(), table, code + "0");
        buildCode(node.getRight(), table, code + "1");
    }

    // 将单词查找树输出到标准输出流
    // 前序遍历
    private static void writeTrie(Node node) {
        if (node.isLeaf()) {
            BinaryStdOut.write(true);
            BinaryStdOut.write(node.getC());
            return;
        }
        BinaryStdOut.write(false);
        writeTrie(node.getLeft());
        writeTrie(node.getRight());
    }

    // 从输入流读取单词查找树
    // 前序遍历
    private static Node readTrie() {
        if (BinaryStdIn.readBoolean()) {
            return new Node(BinaryStdIn.readChar(), EXPAND_FREQ, null, null);
        }
        return new Node(INNER_NODE, EXPAND_FREQ, readTrie(), readTrie());
    }
}