常见的分布函数
二项分布
![alt text]()
几何分布
![alt text]()
超几何分布
![alt text]()
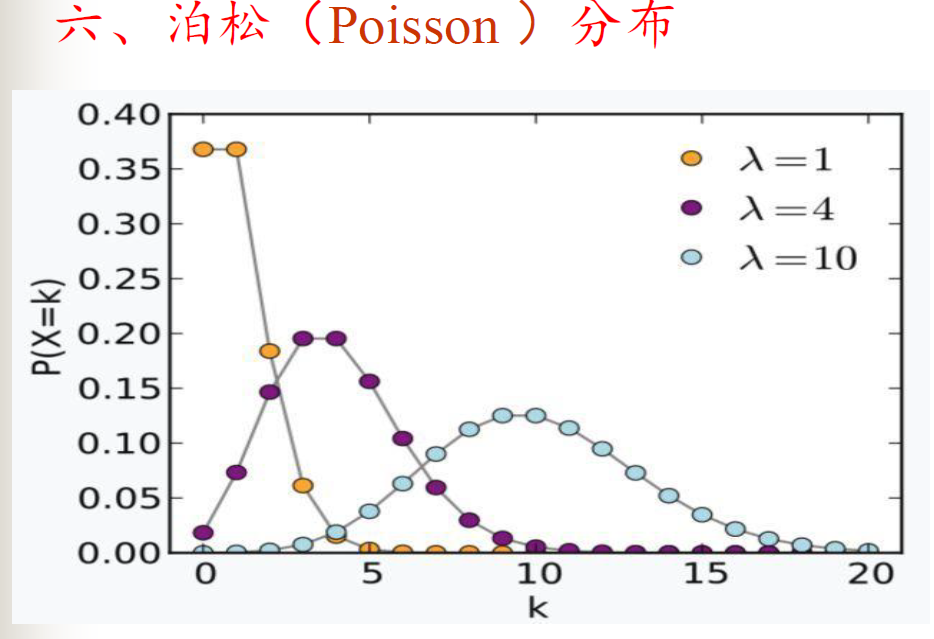
泊松分布
![alt text]()
![alt text]()
均匀分布
![alt text]()
指数分布
![alt text]()
正态分布
![alt text]()
标准正态分布
![alt text]()
![alt text]()
二项分布和泊松分布之间的关系
泊松分布可以看作是二项分布的一种极限形式。当考虑一个二项分布问题,如果试验次数𝑛非常大,而每次试验成功的概率𝑝非常小,但乘积𝑛𝑝(期望值)保持在一个有限的常数𝜆,这时二项分布就可以近似为泊松分布。这意味着,在大量独立的伯努利试验中,如果每次试验成功的概率很小,关注的是成功次数而不是每次试验的具体结果时,泊松分布提供了一个更简便的模型。
在上述极限情况下,泊松分布的参数𝜆实际上等于二项分布中成功次数的期望值𝑛𝑝。这表明泊松分布中的事件发生率𝜆可以直接通过二项分布的参数𝑛和𝑝来确定
二项分布、泊松分布、正态分布的特性
其中的二项分布B和泊松分布P具有可加性
![alt text]()
正态分布之和的特性
![alt text]()
常用函数的期望与方差
![alt text]()
![alt text]()
常用分布函数
正态分布
![alt text]()
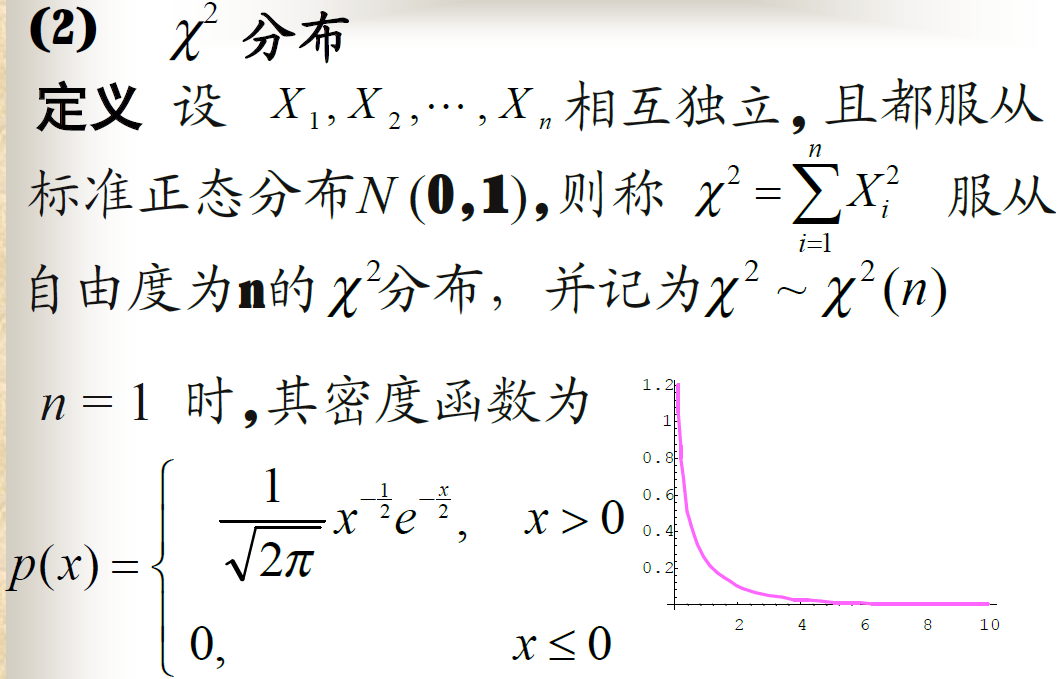
卡方分布
![alt text]()
卡方分布的性质
![alt text]()
t分布
![alt text]()
t分布的性质
![alt text]()
F分布
![alt text]()
![alt text]()
F分布的性质
![alt text]()
经典题目
![alt text]()
![alt text]()
![alt text]()
分布函数与密度函数
分布函数的定义
分布函数是指随机变量小于一个数值x的概率,准确来说分布函数应该叫做累计分布函数
![alt text]()
通常分布函数采用大写字母F来表示,P表示x点发生的概率
从而可以得出以下的性质
![alt text]()
分布函数与密度函数的关系
![alt text]()
![alt text]()
![alt text]()
变量的独立性
![alt text]()
独立的变量相加的方差运算
![alt text]()
两个变量和的分布
![alt text]()
![alt text]()
变量和的分布运算方式与卷积类似
![alt text]()
K阶原点矩与K阶中心距
![alt text]()
原点距可以看成数据点到原点的距离
中心距则是数据到达数据中心点的距离
极差
![alt text]()
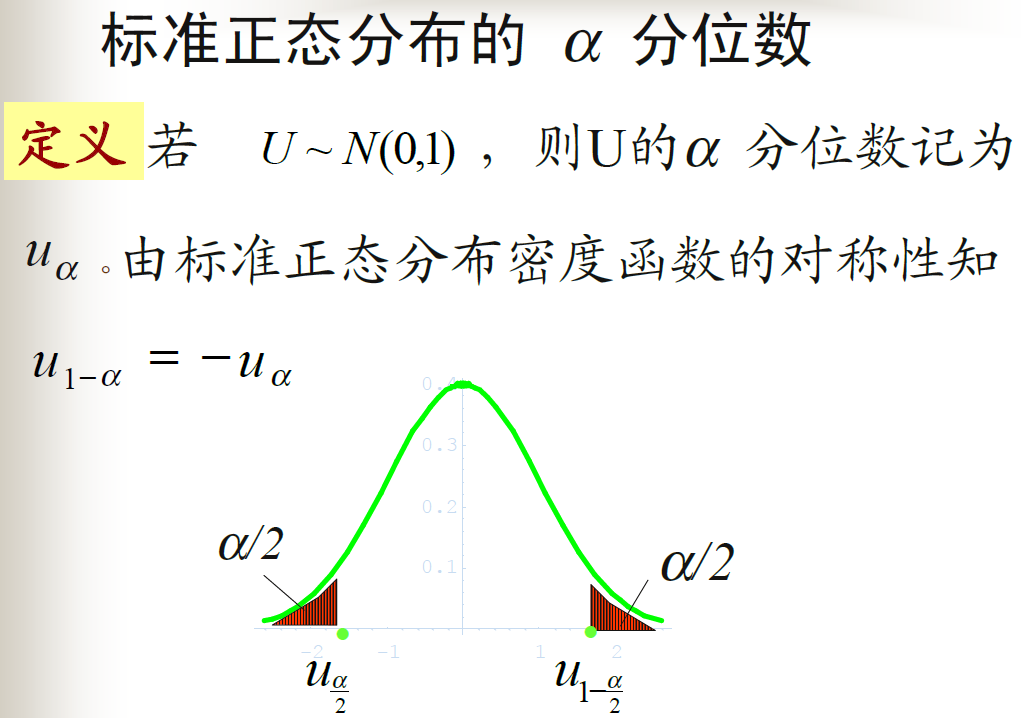
分位数
![alt text]()
![alt text]()
抽样分布
正态总体的抽样分布
![alt text]()
可以看出,抽样后的样本均值符合正态分布,抽样的均值等于总体均值,方差等于总体方差的1/n。
需要注意样本方差与卡方分布的系数中,卡方分布的自由度是n-1
![alt text]()
![alt text]()
![alt text]()
![alt text]()
样本均值
![alt text]()
样本无偏方差
![alt text]()
样本均值的期望
![alt text]()
无偏方差的期望
![alt text]()
![alt text]()
![alt text]()
点估计方法
矩法
矩估计是数理统计中一种常用的参数估计方法,它基于总体的矩(如均值、方差等)与参数之间的关系来进行估计。矩估计的基本思想是利用样本矩来估计相应的总体矩,进而通过总体矩与参数的关系来估计未知参数。这种方法直观、简便,并且适用于多种类型的分布。
![alt text]()
![alt text]()
极大似然估计
极大似然估计(Maximum Likelihood Estimation, MLE)是一种常用的参数估计方法,其核心思想是寻找一组参数值,使得观察到的数据出现的似然性(即概率)最大。换句话说,极大似然估计选择使数据观测值出现概率最大的参数值作为估计值。
![alt text]()
顺序统计量法
![alt text]()
![alt text]()
评价估计量地标准
无偏性
![alt text]()
有效性
![alt text]()
![alt text]()
![alt text]()
![alt text]()
相合性
![alt text]()
置信区间
![alt text]()
![alt text]()
![alt text]()
单侧置信区间
![alt text]()
正态总体参数的置信区间
方差已知,均值的置信区间
![alt text]()
![alt text]()
方差未知,均值的置信区间
![alt text]()
均值已知,方差的置信区间
![alt text]()
![alt text]()
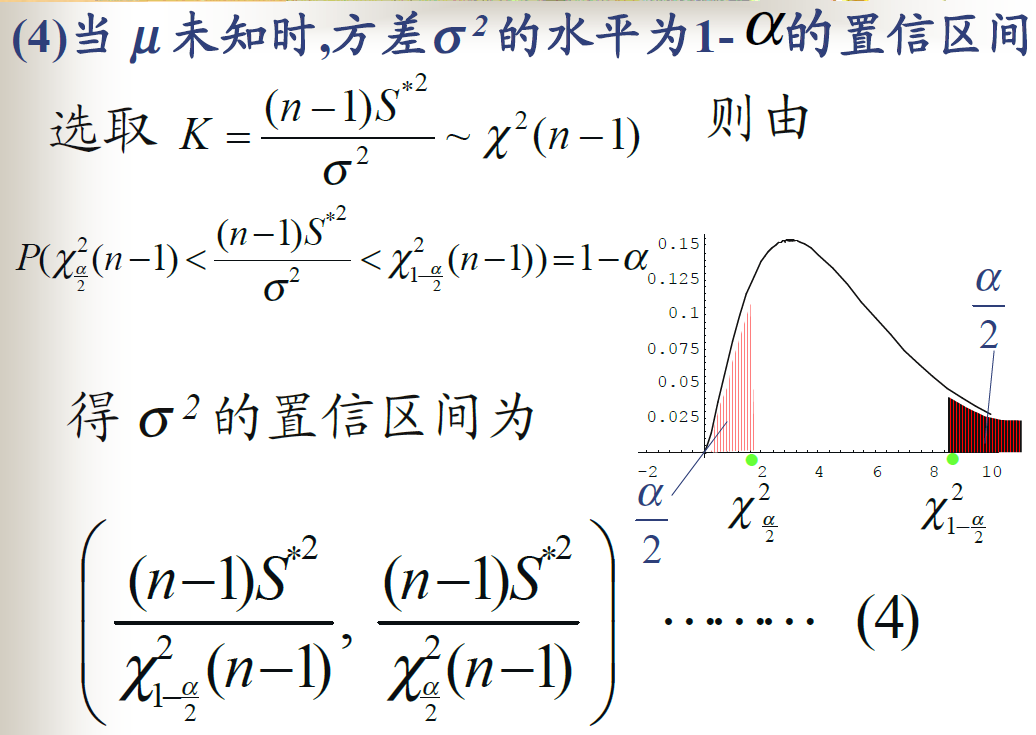
均值未知,方差的置信区间
![alt text]()
两个正态总体的情况
![alt text]()
方差已知,均值的置信区间
![alt text]()
方差未知,均值的置信区间
![alt text]()
![alt text]()
均值已知,方差比的置信区间
![alt text]()
均值未知,方差比的置信区间
![alt text]()
正态总体均值与方差的联合区间估计
![alt text]()
![alt text]()
![alt text]()
0-1分布的参数区间估计
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
假设检验
![alt text]()
![alt text]()
![alt text]()
检验的显著水平与两类错误
![alt text]()
![alt text]()
![alt text]()
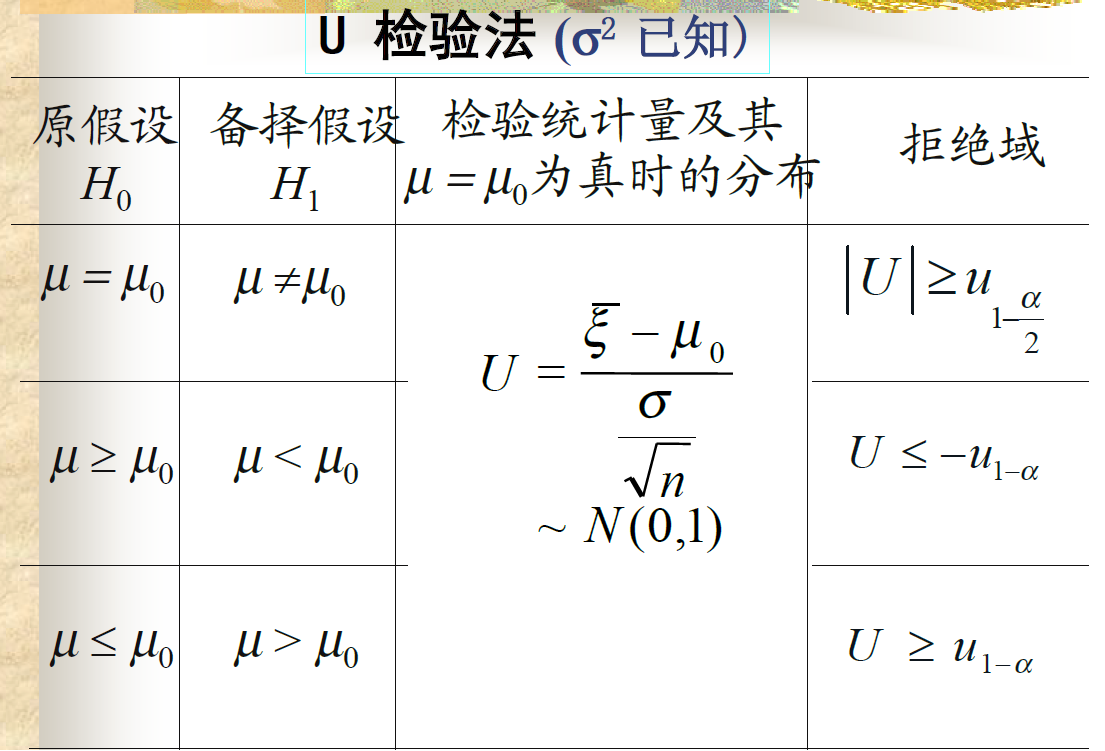
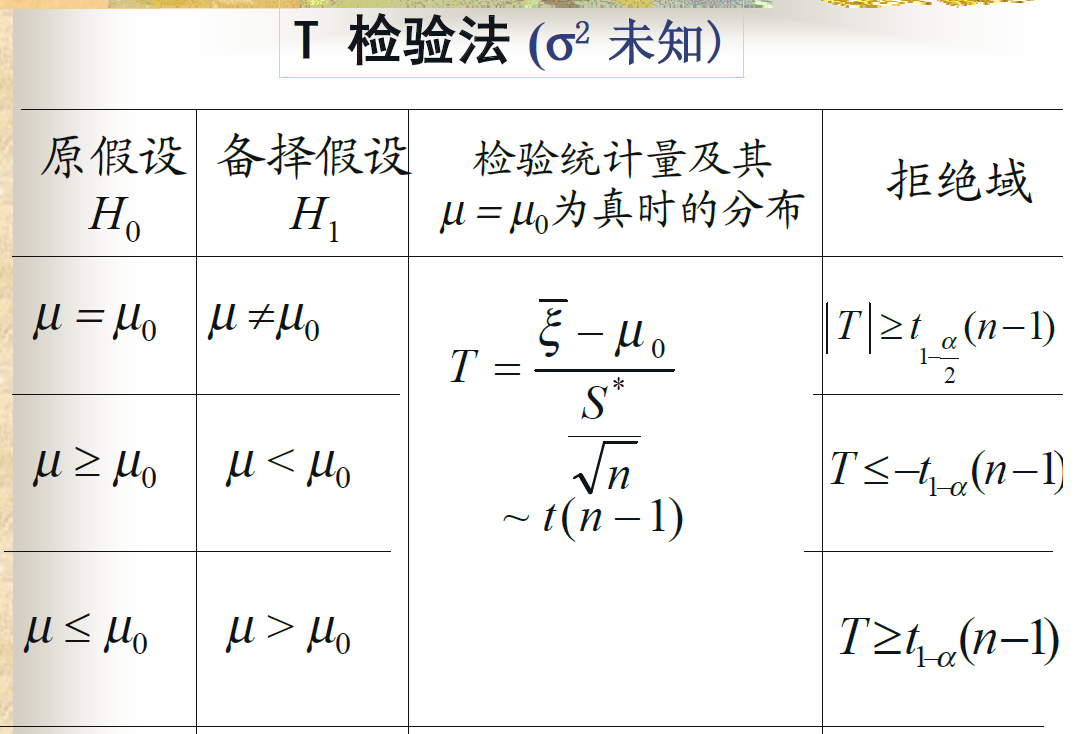
单正态总体的参数假设检验
均值的检验
![alt text]()
![alt text]()
![alt text]()
![alt text]()
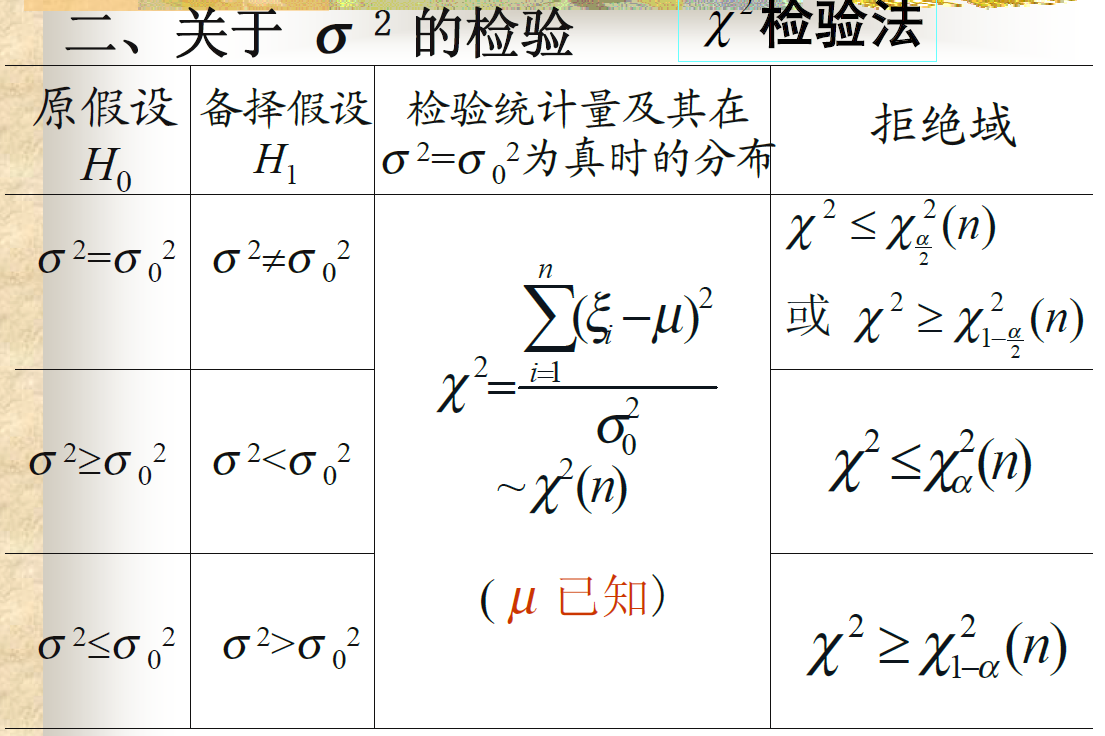
方差的检验
![alt text]()
![alt text]()
两个正态总体的参数假设检验
![alt text]()
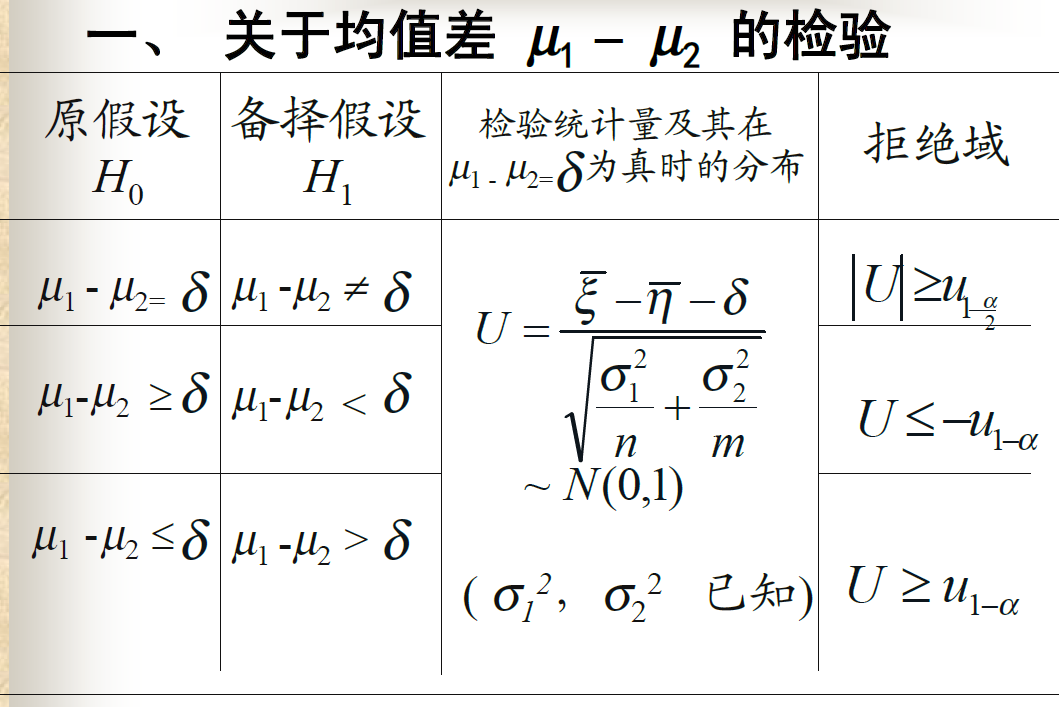
均值差的检验
![alt text]()
![alt text]()
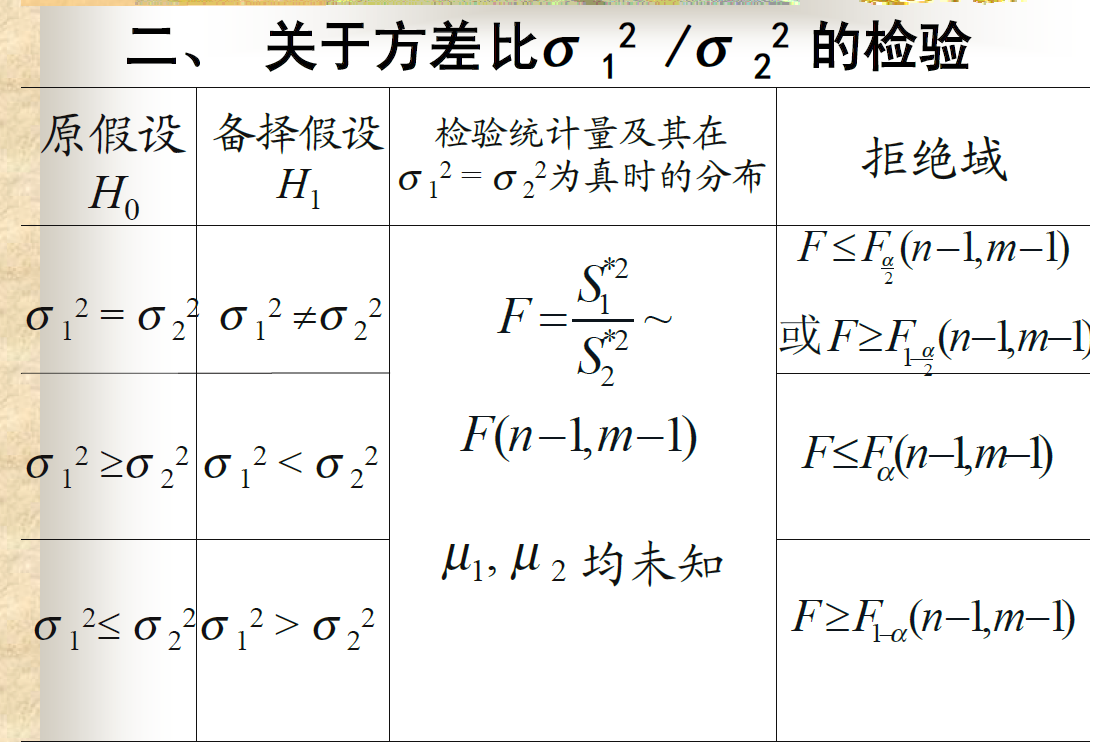
方差比的检验
![alt text]()
![alt text]()
非正态总体均值的假设检验
方差已知时总体均值的假设检验
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
方差未知时总体均值的假设检验
![alt text]()
![alt text]()
![alt text]()
方差已知时两个总体均值的假设
![alt text]()
![alt text]()
![alt text]()
方差未知时两个总体均值的假设
![alt text]()
![alt text]()
分布拟合检验
卡方检验
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
独立性检验
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
两个总体相等性检验
![alt text]()
符号检验法
![alt text]()
![alt text]()
![alt text]()
秩和检验法
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
游程检验法
![alt text]()
![alt text]()
![alt text]()
![alt text]()
回归分析
一元线性回归
![alt text]()
![alt text]()
最小二乘法
![alt text]()
![alt text]()
![alt text]()
![alt text]()
最小二乘法中a,b两个参数计算推导过程
线性回归的基本概念
线性回归模型假定因变量 \(y\) 与自变量 \(x\) 之间存在线性关系,可以表示为:
\[y = a + bx + \epsilon
\]
其中, \(a\) 是截距,\(b\) 是回归系数, \(\epsilon\) 是误差项。
最小二乘法的目标
最小二乘法(Ordinary Least Squares, OLS)的目标是找到 \(a\) 和 \(b\) 使得观测值 \(y_i\) 与预测值 \(\hat{y}_i\) 之间的误差平方和最小。即:
$ \hat{y}_i = a + bx_i $
定义误差平方和(Sum of Squared Errors, SSE)为:
\[SSE = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} \left( y_i - (a + bx_i) \right)^2
\]
对 \(a\) 和 \(b\) 求导
我们通过对 \(SSE\) 关于 \(a\) 和 \(b\) 求偏导数,并令其等于零,以找到使 \(SSE\) 最小的 \(a\) 和 \(b\)。
- 对 \(a\) 求偏导数:
\[\frac{\partial SSE}{\partial a} = \sum_{i=1}^{n} 2 \left( y_i - (a + bx_i) \right) \cdot (-1) = -2 \sum_{i=1}^{n} \left( y_i - a - bx_i \right)
\]
令其等于零:
\[\sum_{i=1}^{n} \left( y_i - a - bx_i \right) = 0
\]
\[\sum_{i=1}^{n} y_i - na - b \sum_{i=1}^{n} x_i = 0
\]
\[na + b \sum_{i=1}^{n} x_i = \sum_{i=1}^{n} y_i
\]
- 对 $ b $ 求偏导数:
\[\frac{\partial SSE}{\partial b} = \sum_{i=1}^{n} 2 \left( y_i - (a + bx_i) \right) \cdot (-x_i) = -2 \sum_{i=1}^{n} x_i \left( y_i - a - bx_i \right)
\]
令其等于零:
\[\sum_{i=1}^{n} x_i \left( y_i - a - bx_i \right) = 0
\]
\[\sum_{i=1}^{n} x_i y_i - a \sum_{i=1}^{n} x_i - b \sum_{i=1}^{n} x_i^2 = 0
\]
\[a \sum_{i=1}^{n} x_i + b \sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} x_i y_i
\]
联立方程求解 $ a $ 和 $ b $
得到方程组:
\[na + b \sum_{i=1}^{n} x_i = \sum_{i=1}^{n} y_i
\]
\[a \sum_{i=1}^{n} x_i + b \sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} x_i y_i
\]
- 先求 $ b $:
记:
\[\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
\]
\[\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i
\]
则方程组改写为:
\[n \bar{y} = na + b \sum_{i=1}^{n} x_i
\]
\[n \bar{y} = na + bn \bar{x}
\]
\[\bar{y} = a + b \bar{x}
\]
利用第二个方程:
\[a \sum_{i=1}^{n} x_i + b \sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} x_i y_i
\]
代入 ( a = \bar{y} - b \bar{x} ):
\[(\bar{y} - b \bar{x}) \sum_{i=1}^{n} x_i + b \sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} x_i y_i
\]
\[\bar{y} \sum_{i=1}^{n} x_i - b \bar{x} \sum_{i=1}^{n} x_i + b \sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} x_i y_i
\]
\[\bar{y} \sum_{i=1}^{n} x_i + b \left( \sum_{i=1}^{n} x_i^2 - \bar{x} \sum_{i=1}^{n} x_i \right) = \sum_{i=1}^{n} x_i y_i
\]
整理得:
\[b = \frac{\sum_{i=1}^{n} x_i y_i - \bar{y} \sum_{i=1}^{n} x_i}{\sum_{i=1}^{n} x_i^2 - \bar{x} \sum_{i=1}^{n} x_i}
\]
- 再求 \(a\):
从上面推导出的关系:
\[a = \bar{y} - b \bar{x}
\]
最终回归系数公式
\(b = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i-1}^{n} (x_i - \bar{x})^2}\)
\(a = \bar{y} - b \bar{x}\)
通过上述步骤,推导了最小二乘法的线性回归方程中的回归系数 ( b ) 和截距 ( a ) 的公式。
最小二乘法的相关性质
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
线性回归效果显著性检验
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
F检验法
![alt text]()
![alt text]()
t检验法
![alt text]()
![alt text]()
未知参数a,b和方差的区间估计
![alt text]()
![alt text]()
![alt text]()
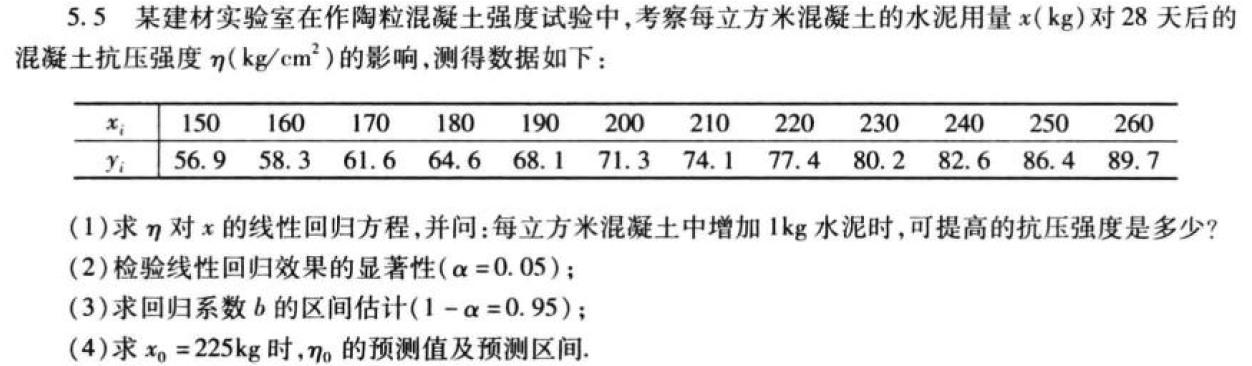
例题
![alt text]()
要解答这道数理统计题目,我们需要进行线性回归分析。具体步骤如下:
A. 求 $ \eta $ 对 $ x $ 的线性回归方程
给定数据:
\[\begin{array}{c|cccccccccc}
x_i & 150 & 160 & 170 & 180 & 190 & 200 & 210 & 220 & 230 & 240 \\
\hline
y_i & 56.9 & 58.3 & 61.6 & 64.6 & 68.1 & 71.3 & 74.1 & 77.4 & 80.2 & 82.6
\end{array}
\]
- 计算 $ \bar{x} $ 和 $ \bar{y} $:
\[\bar{x} = \frac{1}{10} \sum_{i=1}^{10} x_i = \frac{150 + 160 + 170 + 180 + 190 + 200 + 210 + 220 + 230 + 240}{10} = 195
\]
\[\bar{y} = \frac{1}{10} \sum_{i=1}^{10} y_i = \frac{56.9 + 58.3 + 61.6 + 64.6 + 68.1 + 71.3 + 74.1 + 77.4 + 80.2 + 82.6}{10} = 69.51
\]
- 计算 $ S_{xy} $ 和 $ S_{xx} $:
\[S_{xy} = \sum_{i=1}^{10} (x_i - \bar{x})(y_i - \bar{y}) = (150 - 195)(56.9 - 69.51) + (160 - 195)(58.3 - 69.51) + \cdots + (240 - 195)(82.6 - 69.51)
\]
\[S_{xx} = \sum_{i=1}^{10} (x_i - \bar{x})^2 = (150 - 195)^2 + (160 - 195)^2 + \cdots + (240 - 195)^2
\]
- 计算回归系数 \(b\) 和截距 \(a\):
\[b = \frac{S_{xy}}{S_{xx}}
\]
\[a = \bar{y} - b \bar{x}
\]
B. 检验线性回归效果的显著性 (\(\alpha = 0.05\))
- 计算回归平方和 \(SSR\) 和残差平方和 \(SSE\):
\[SSR = b^2 \cdot S_{xx}
\]
\[SSE = \sum_{i=1}^{10} (y_i - \hat{y}_i)^2
\]
- 计算均方误差 \(MSE\):
\[MSE = \frac{SSE}{n-2}
\]
- 利用 F 检验:
\[F = \frac{SSR}{MSE}
\]
查表得到临界值 $ F_{0.05,1,n-2} $,与计算出的 F 值比较。
C. 求回归系数 $ b $ 的区间估计 $ (1 - \alpha = 0.95) $
- 计算标准误差 $ SE_b $:
\[SE_b = \sqrt{\frac{MSE}{S_{xx}}}
\]
- 利用 t 分布确定区间:
\[b \pm t_{0.025,n-2} \cdot SE_b
\]
D. 求 $ x_0 = 225kg $ 时,$ \eta_0 $ 的预测值及预测区间
- 预测值 $ \hat{y}_0 $:
\[\hat{y}_0 = a + b x_0
\]
- 预测区间:
\[\hat{y}_0 \pm t_{0.025,n-2} \cdot \sqrt{MSE \left( 1 + \frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{xx}} \right)}
\]
方差分析
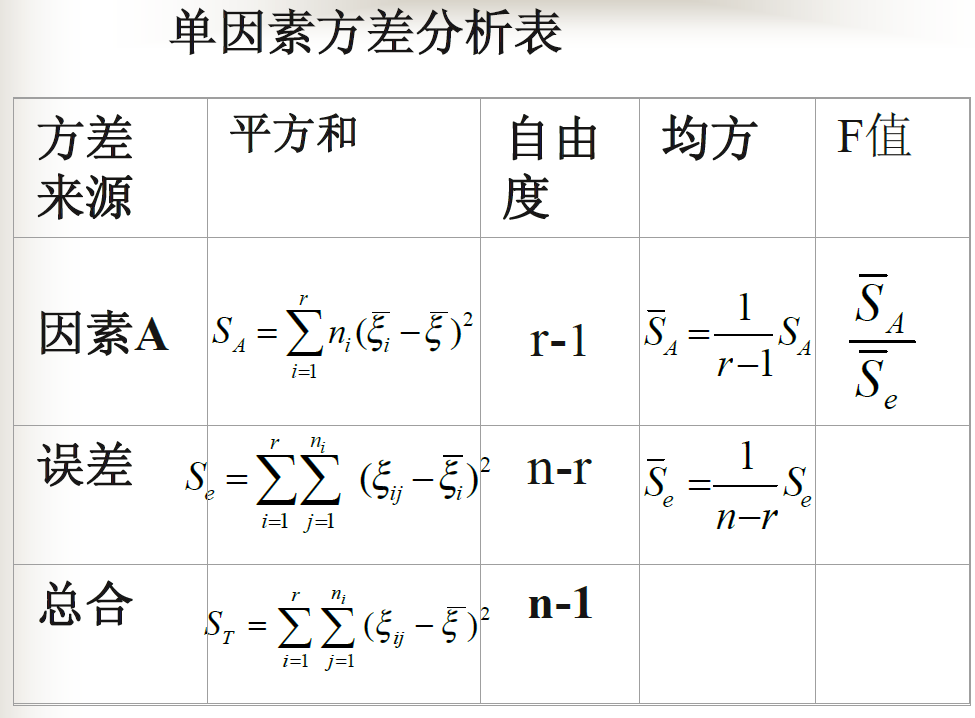
单因子模型
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
显著性检验
![alt text]()
![alt text]()
![alt text]()
参数的估计
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
多重比较
![alt text]()
![alt text]()
![alt text]()
齐次性检验
![alt text]()
![alt text]()
![alt text]()
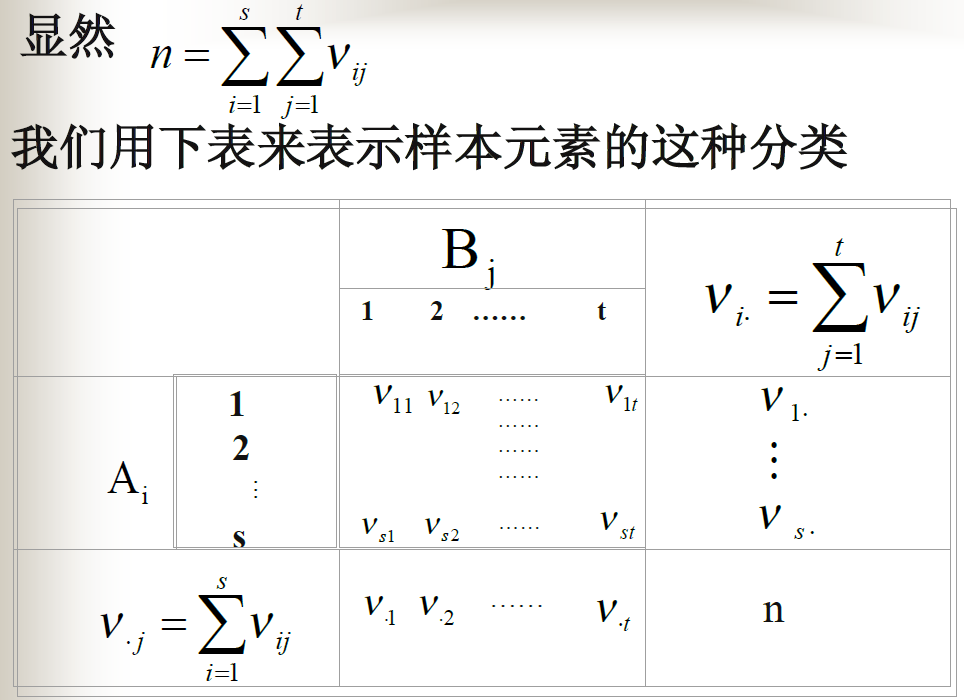
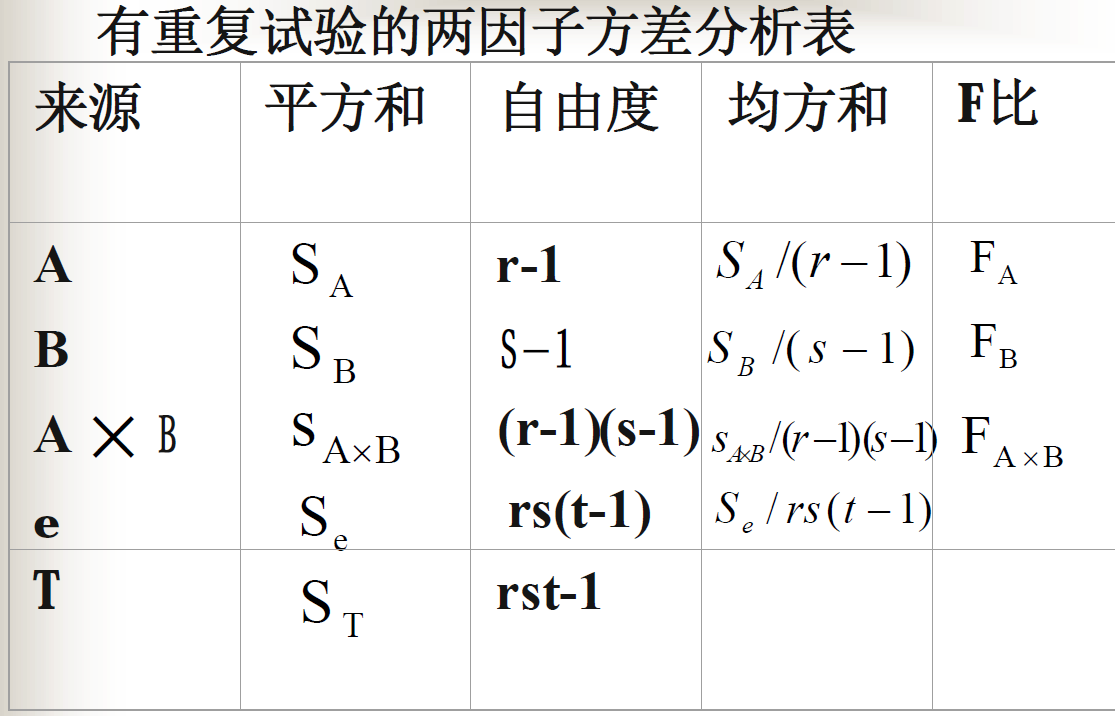
两个因素的方差分析
有交互作用的方差分析模型
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
![alt text]()
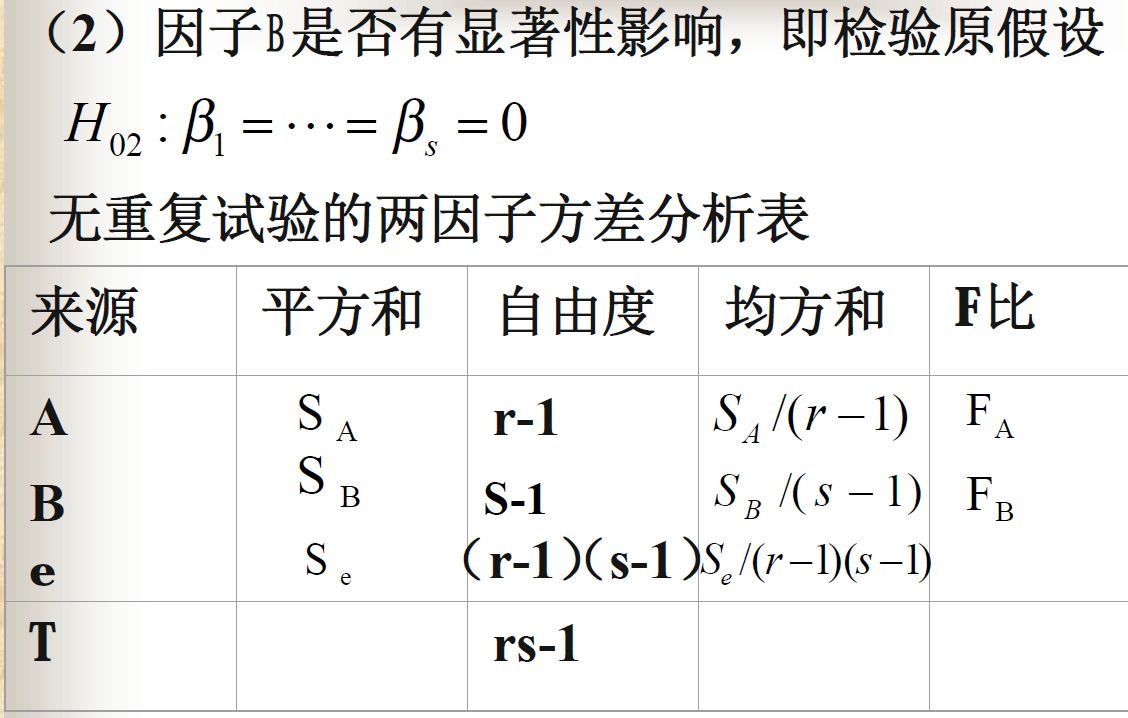
无交互作用无重复试验的方差分析模型
![alt text]()
![alt text]()
![alt text]()
![alt text]()
附录
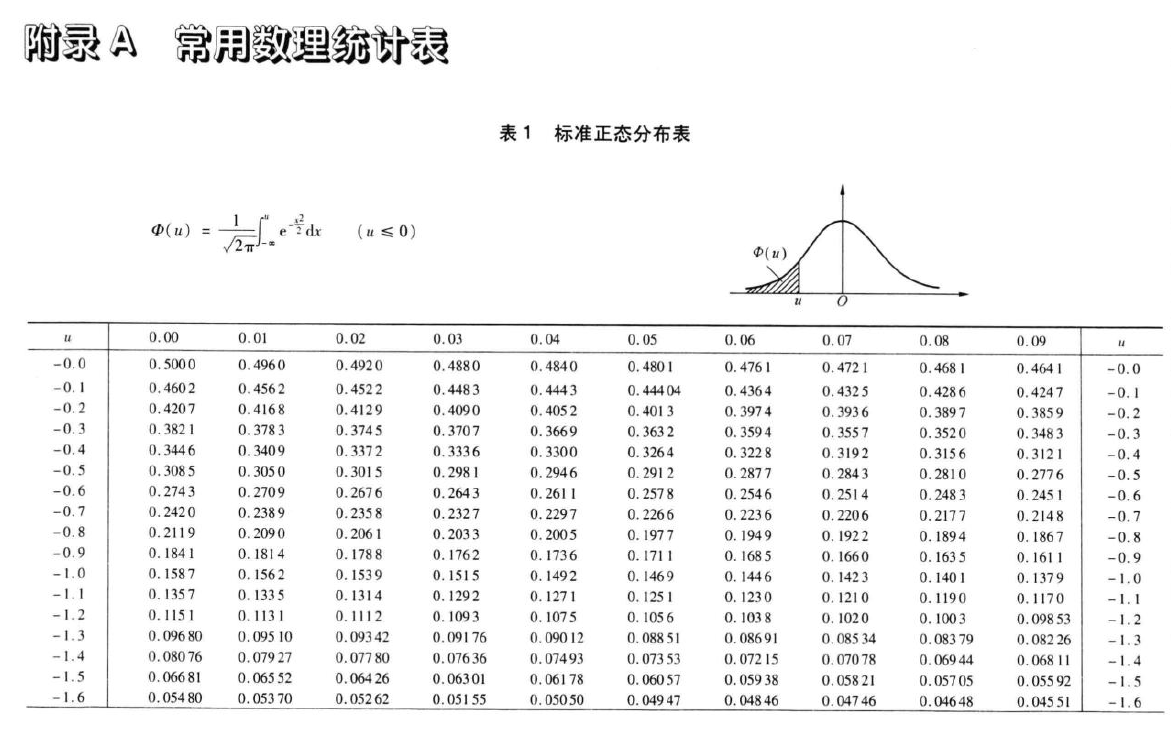
正态分布的积分表
![alt text]()
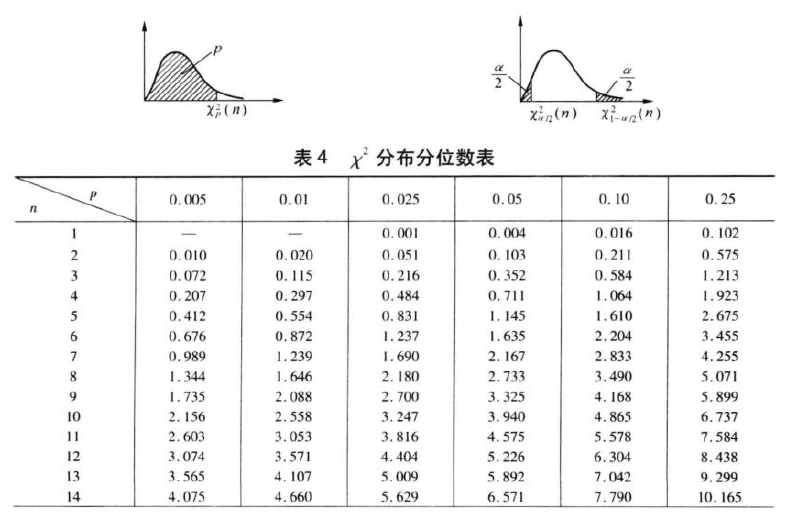
卡方分布表
![alt text]()












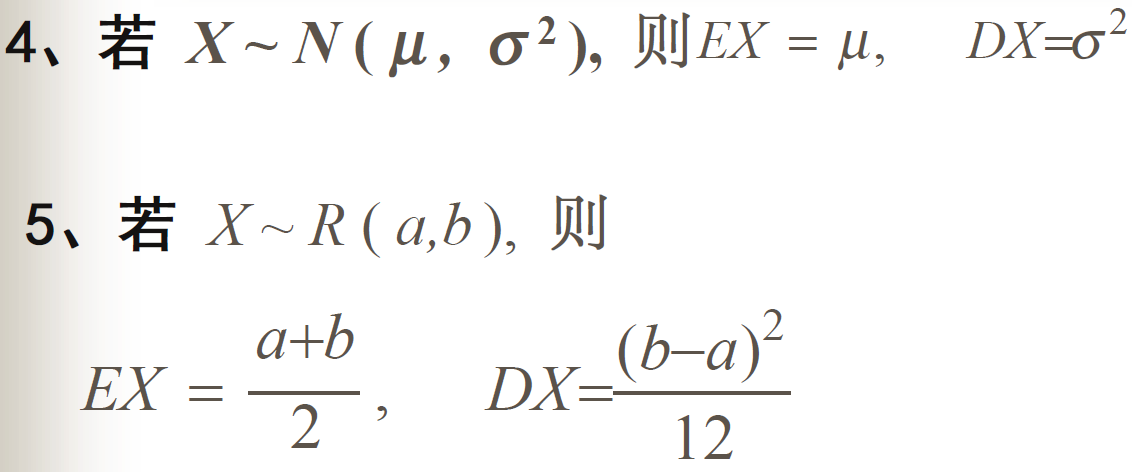





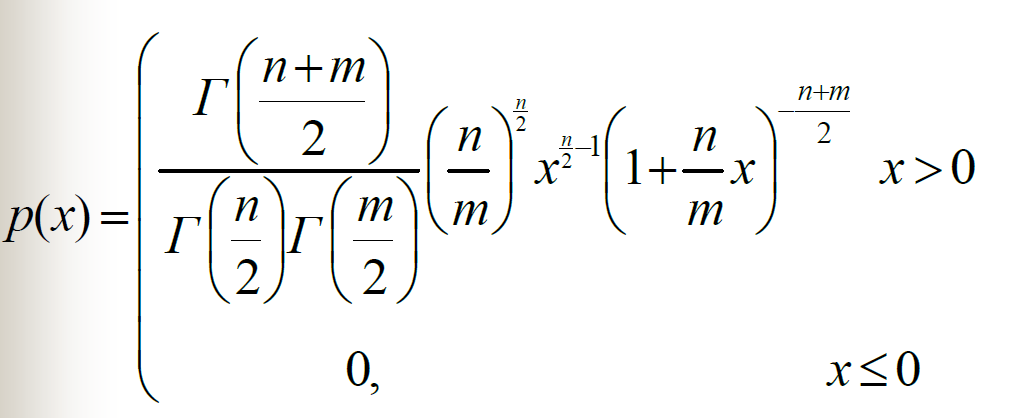

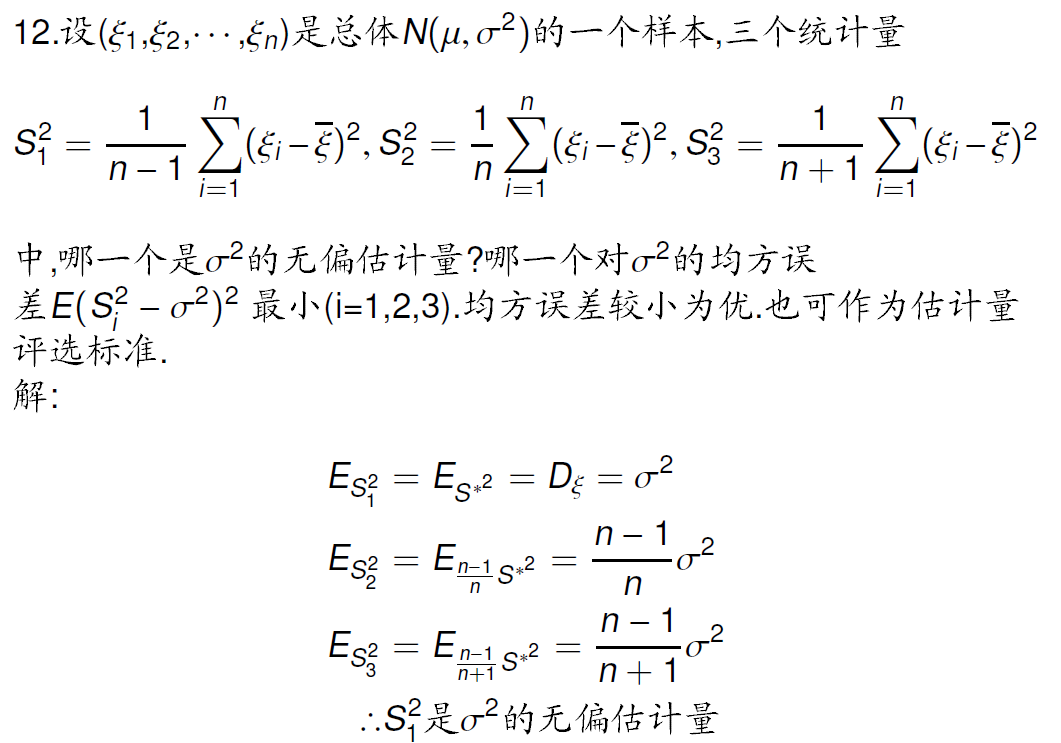
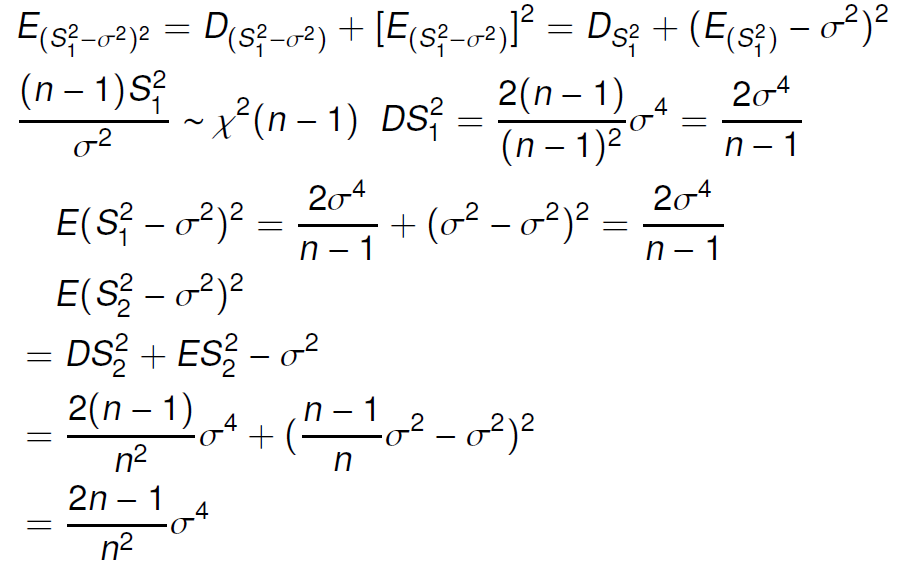









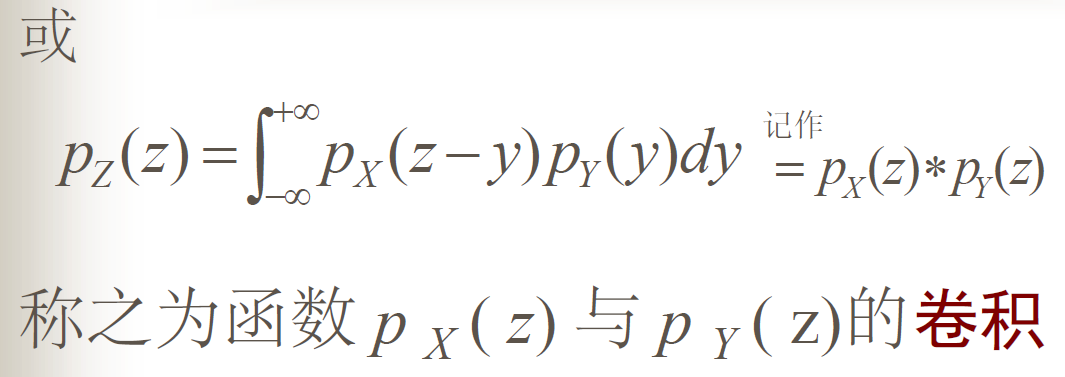







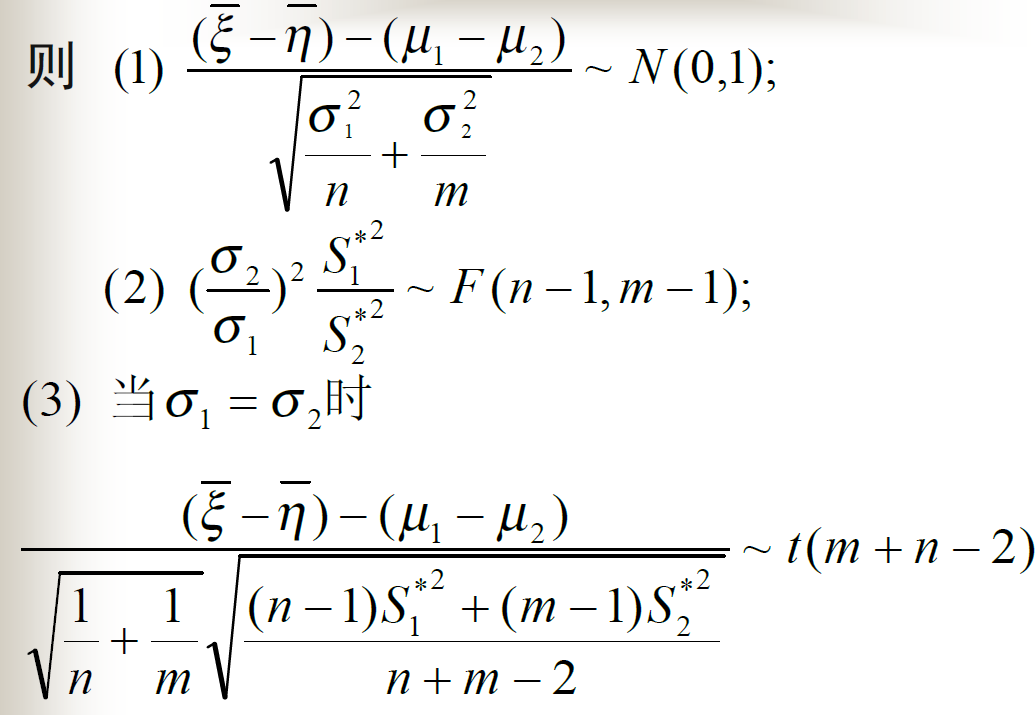

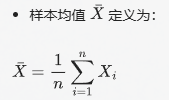
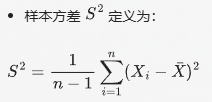
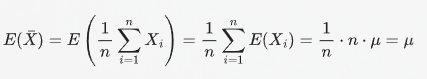


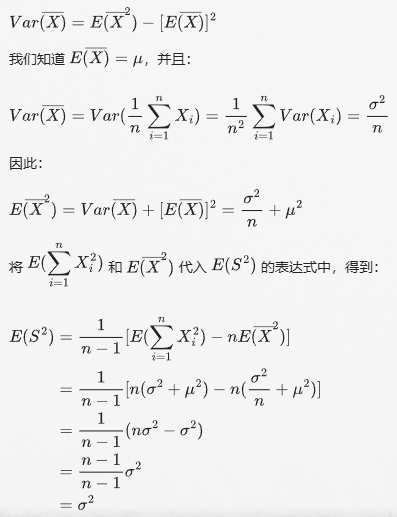



















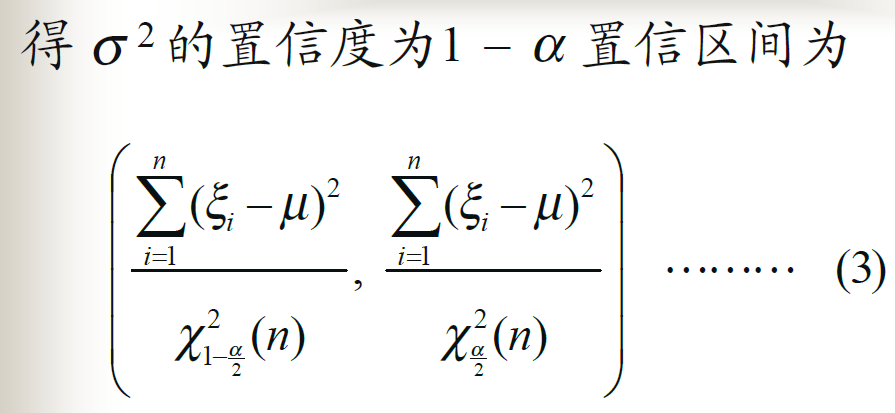








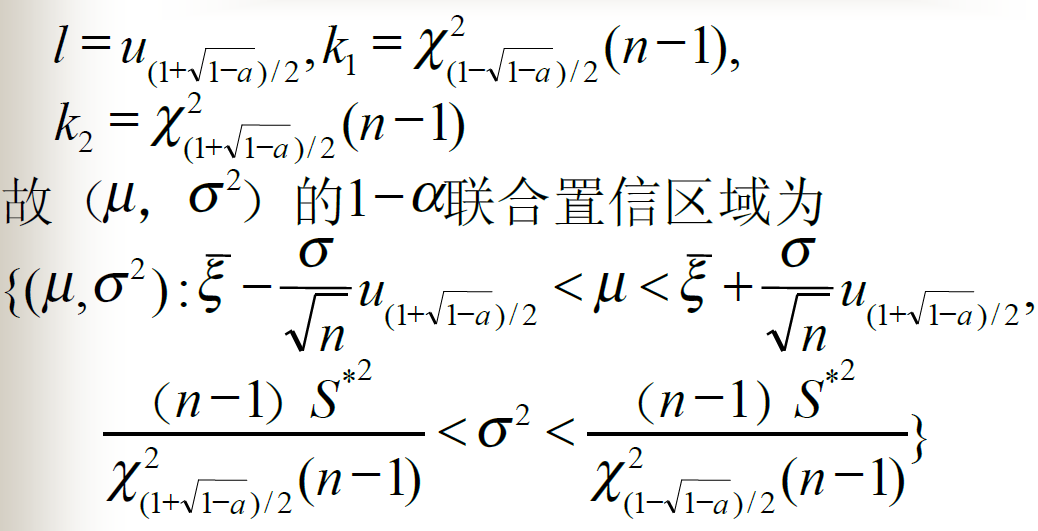

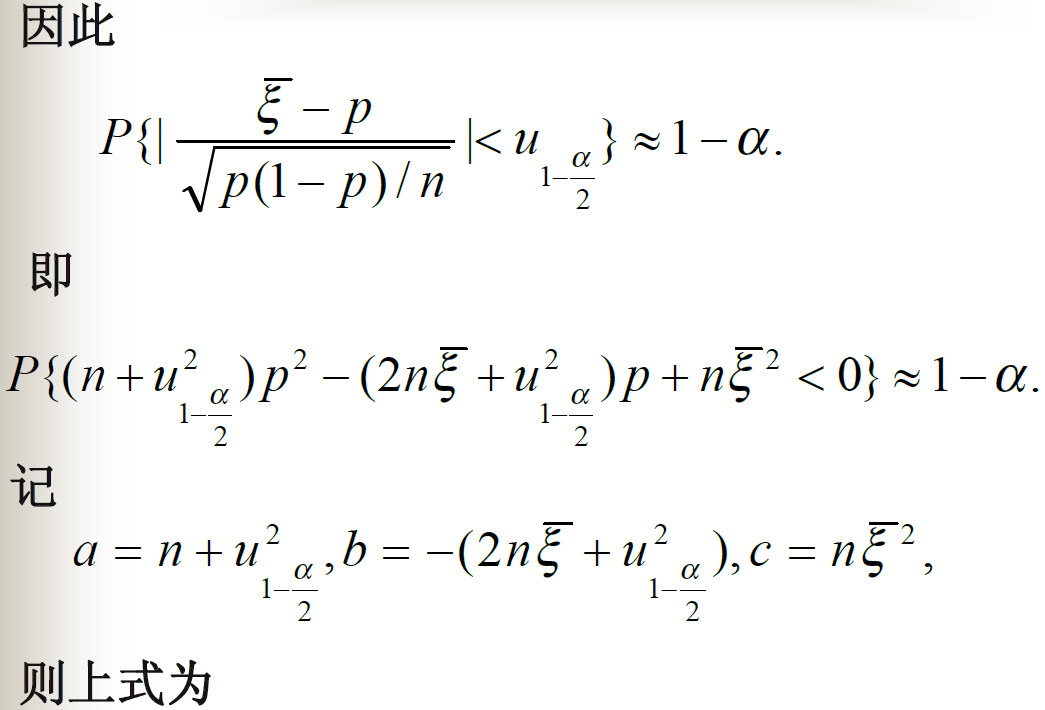



















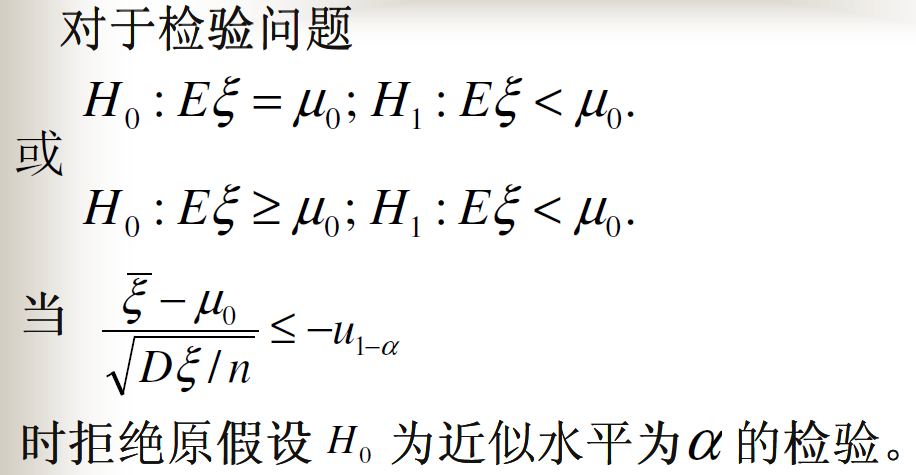




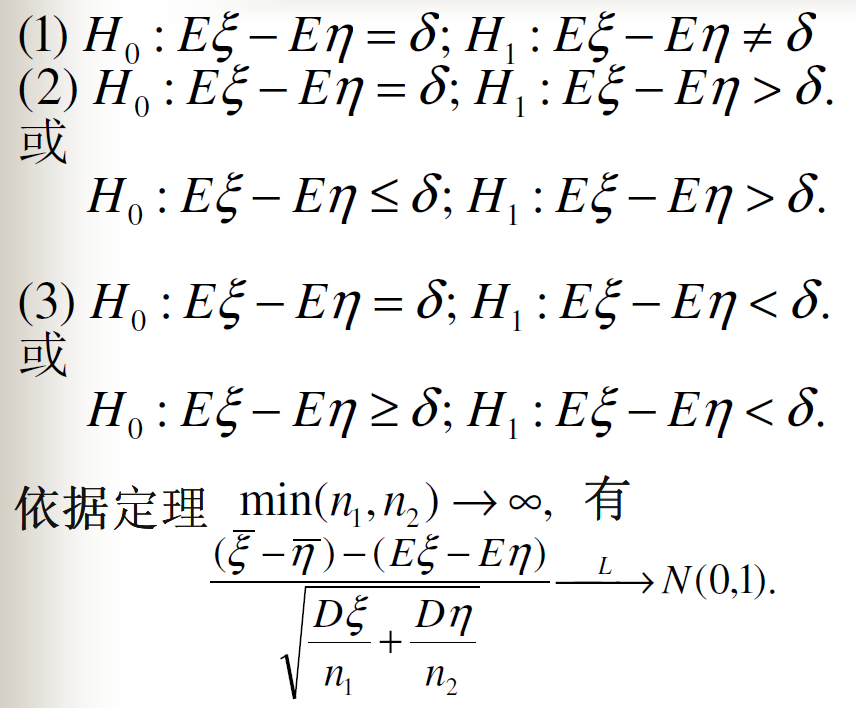
































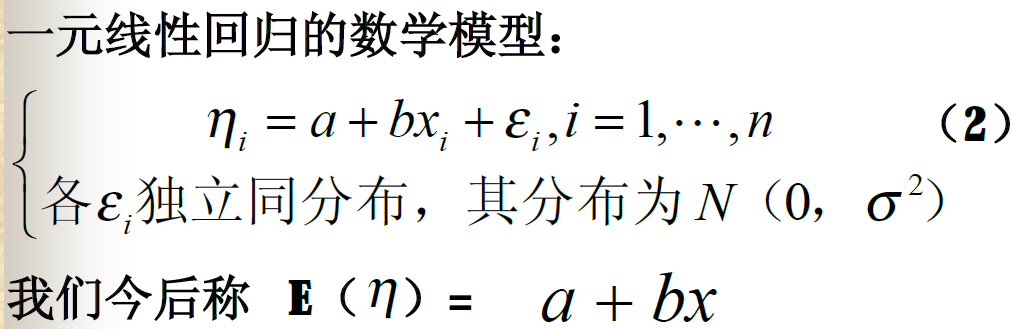


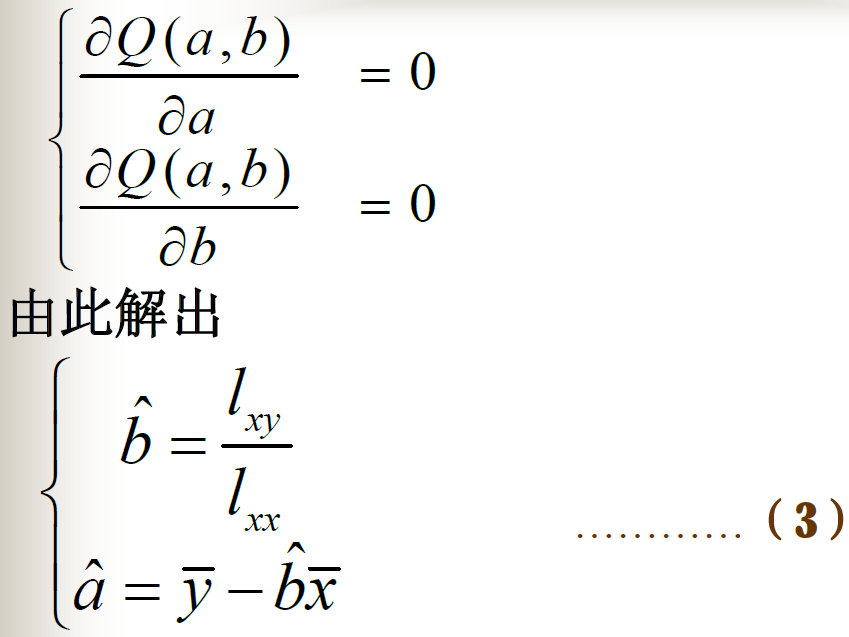



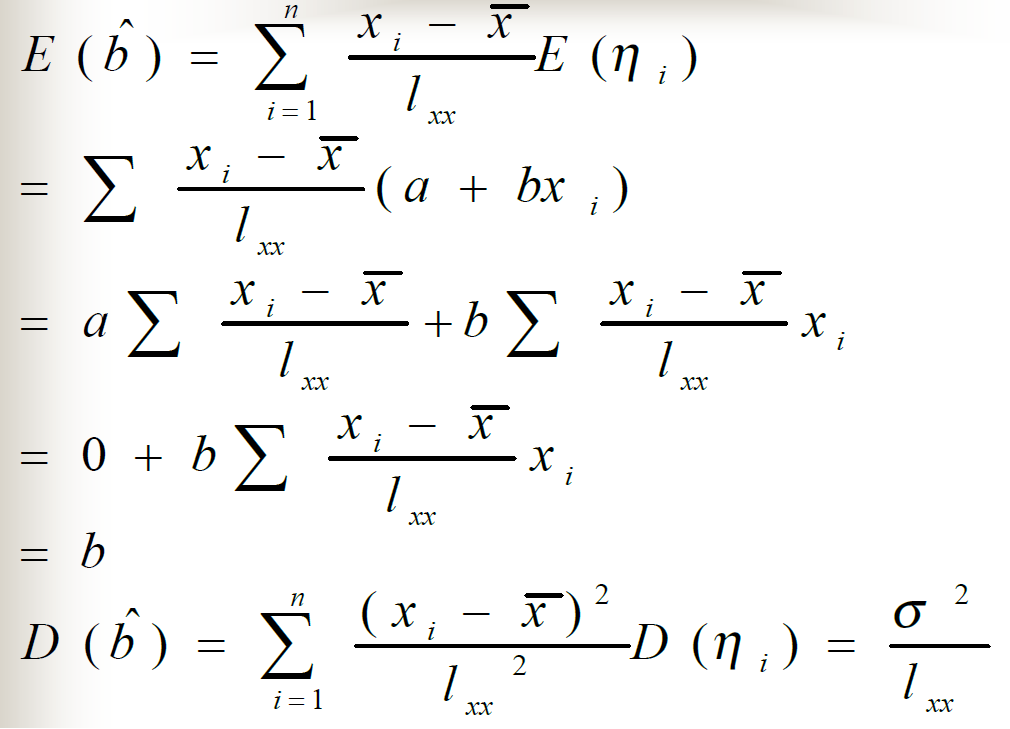

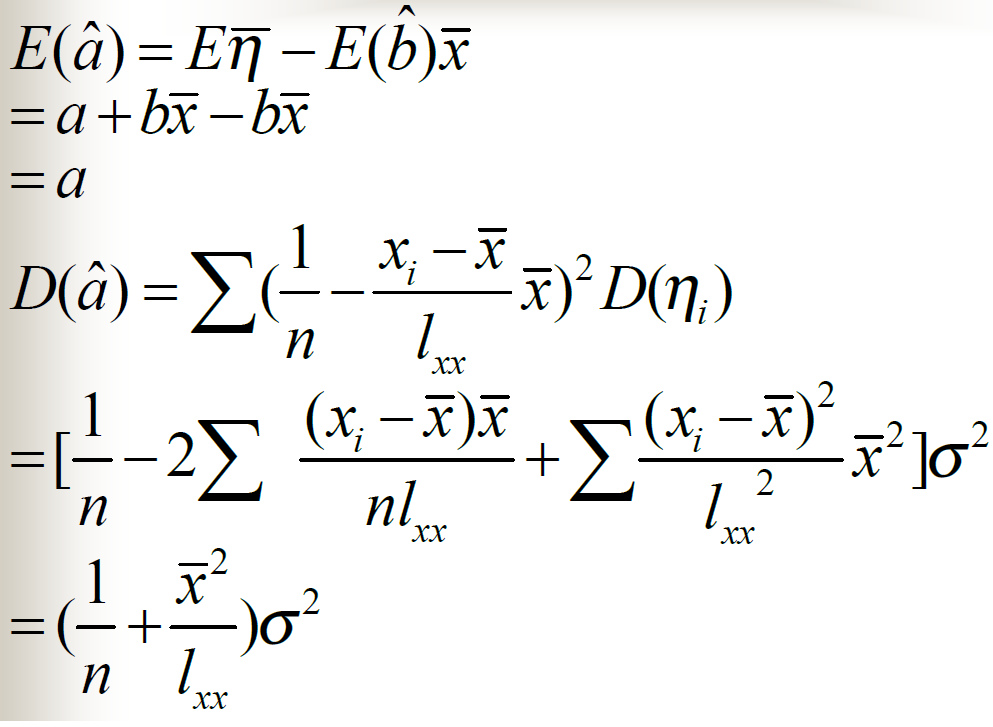
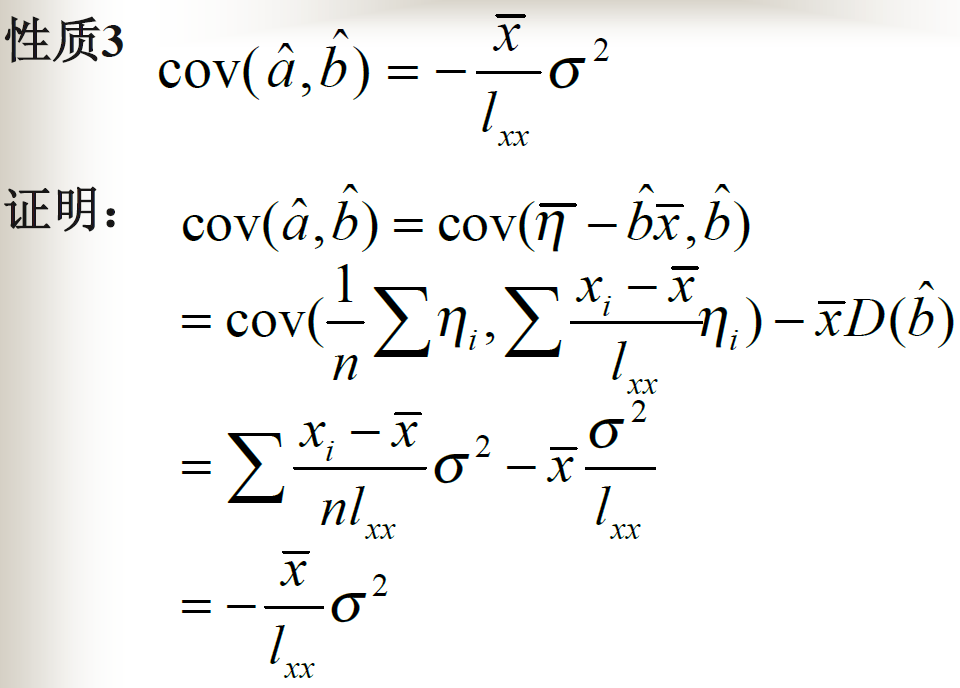

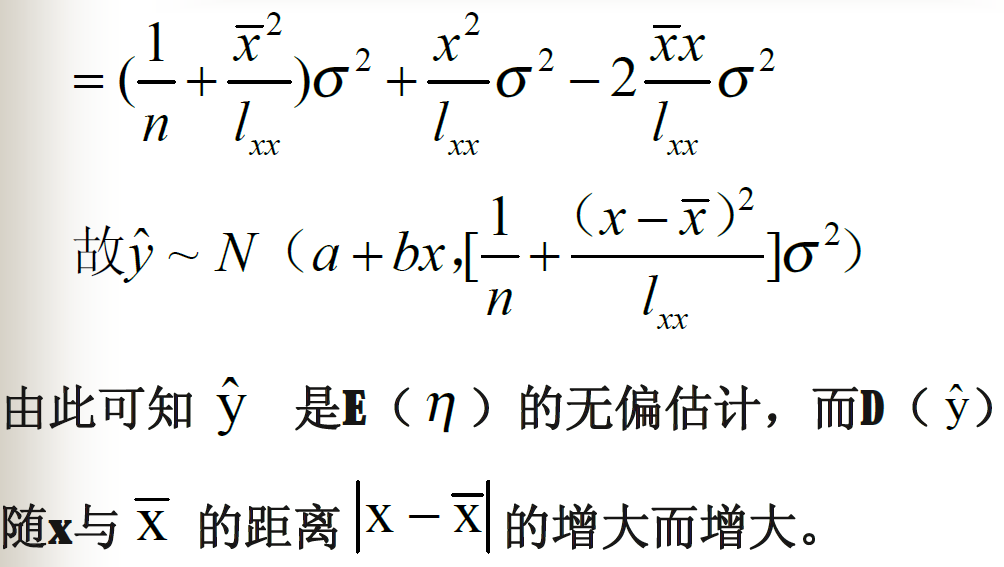




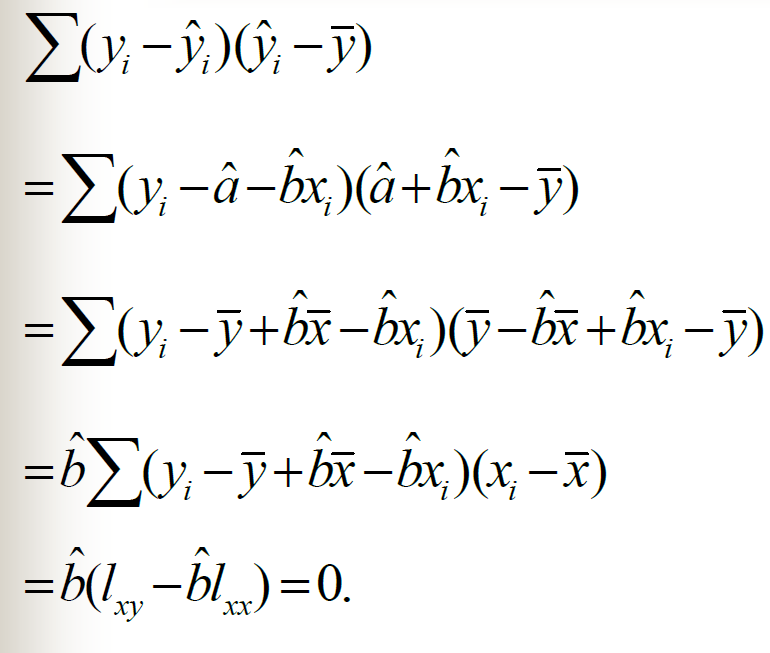
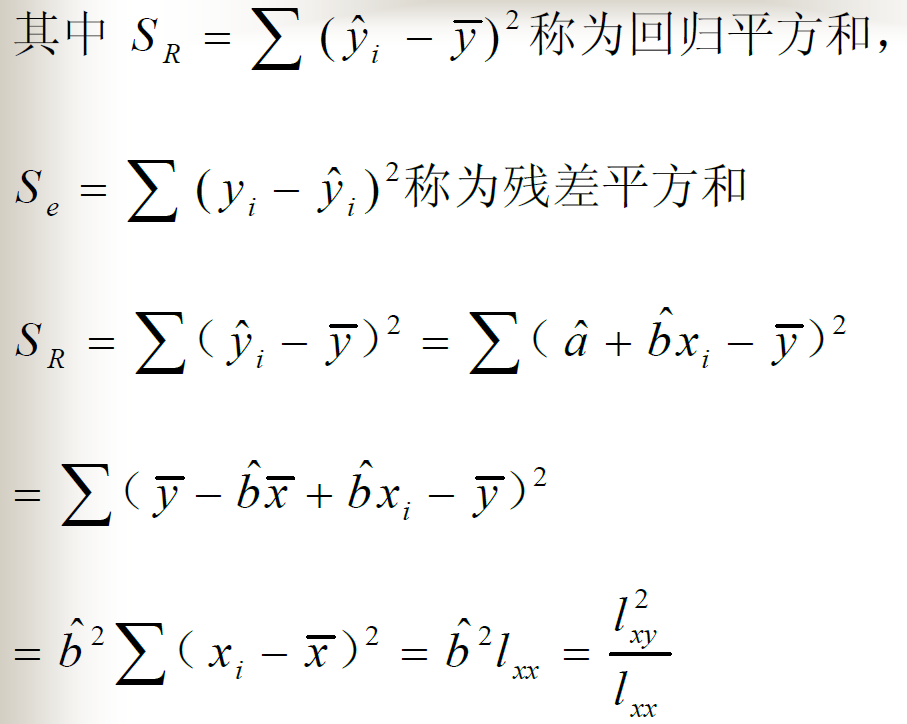

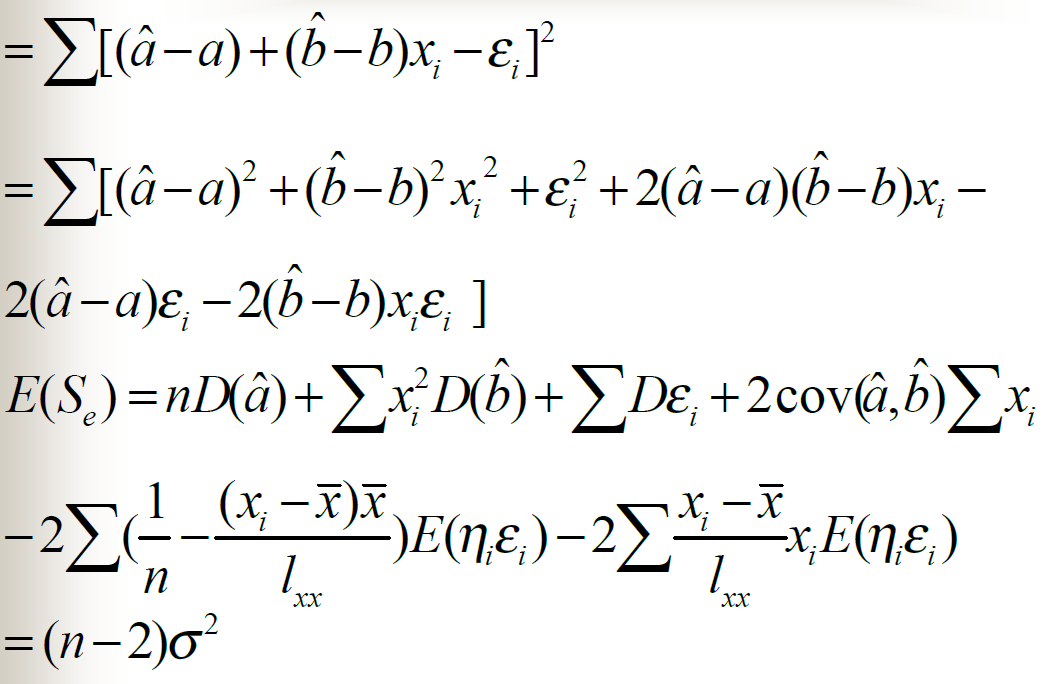







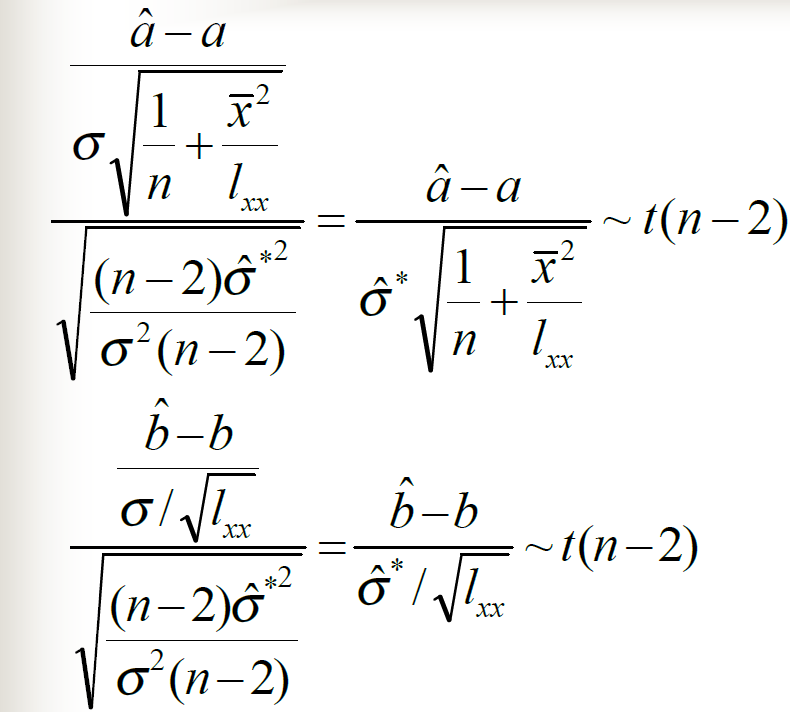



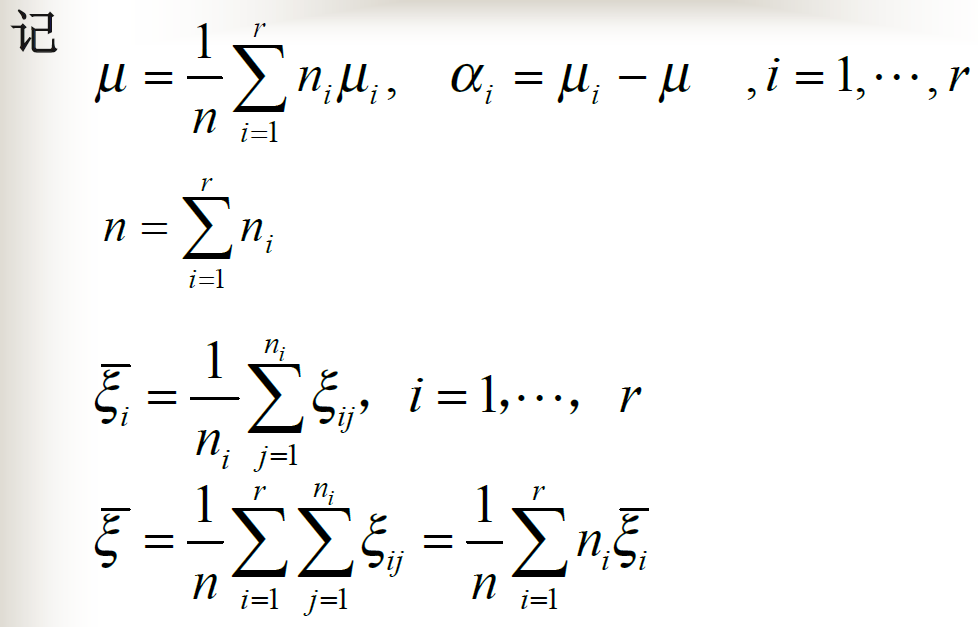




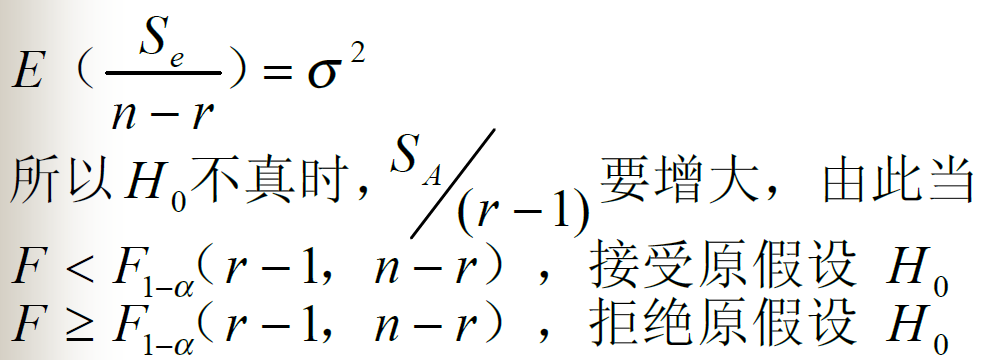

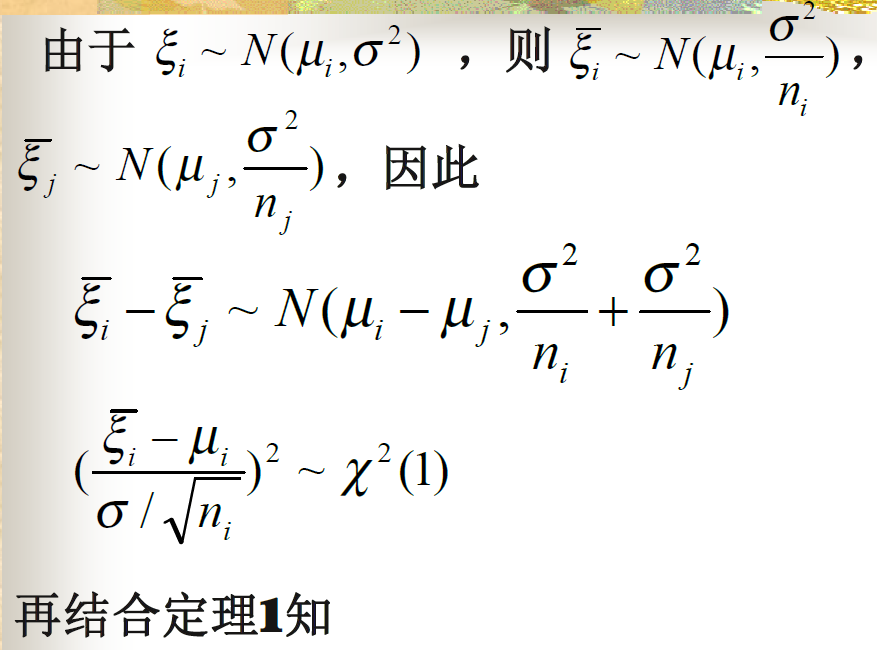
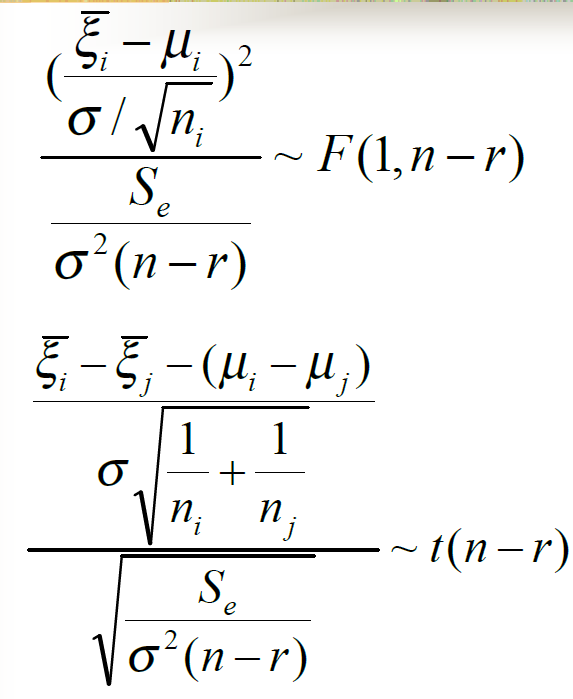



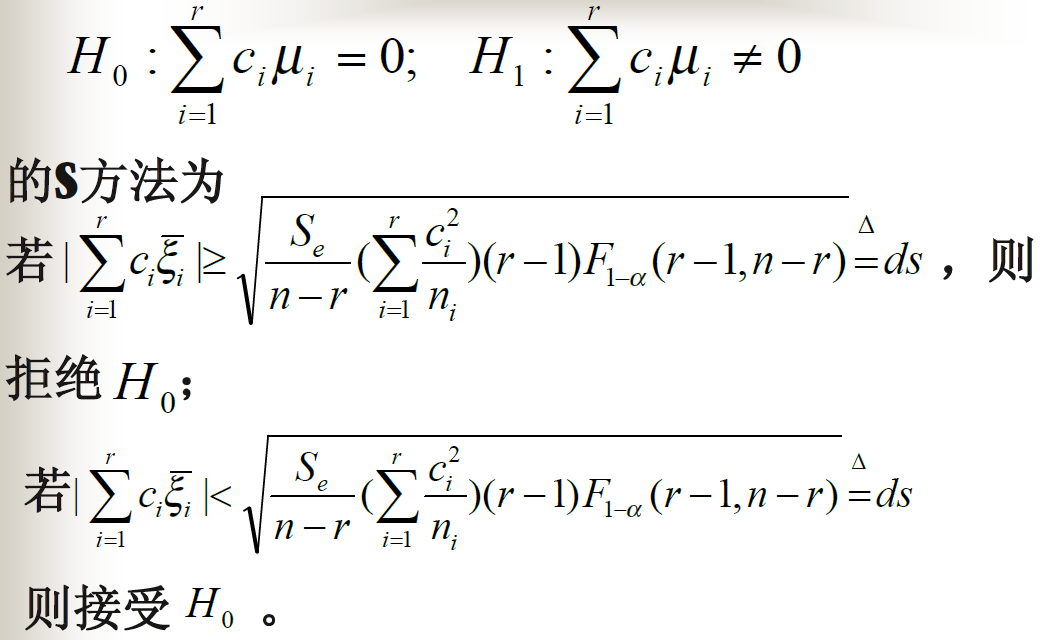


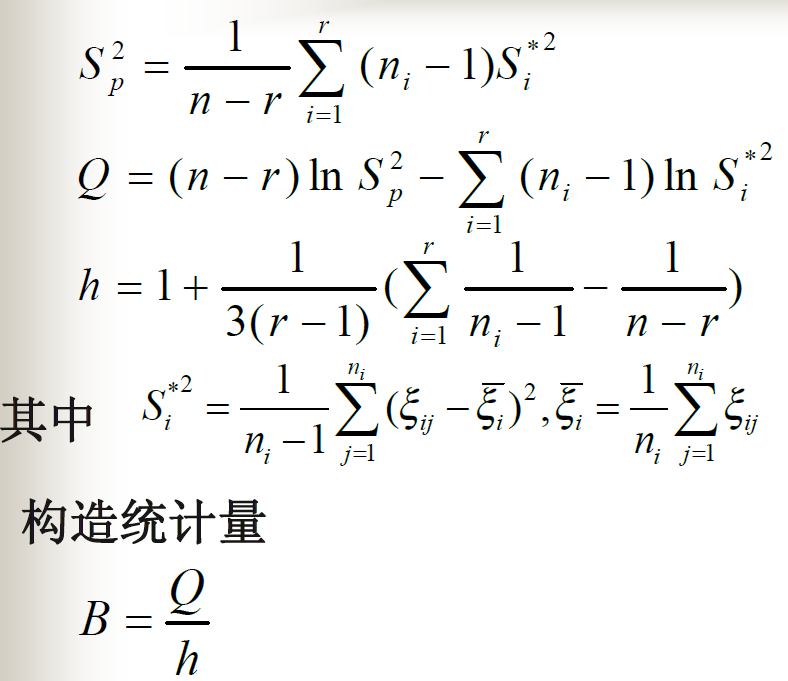






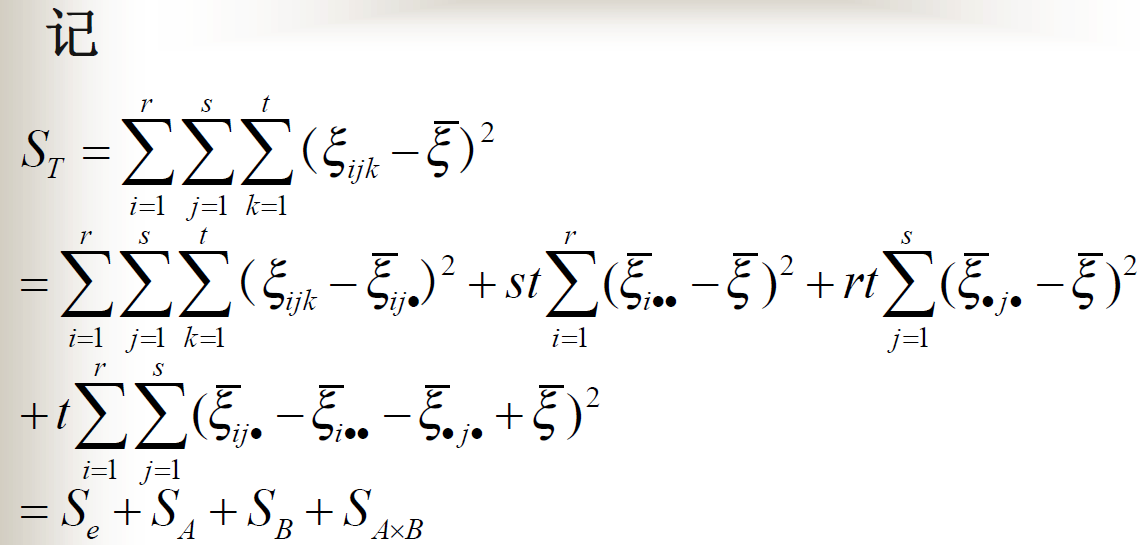
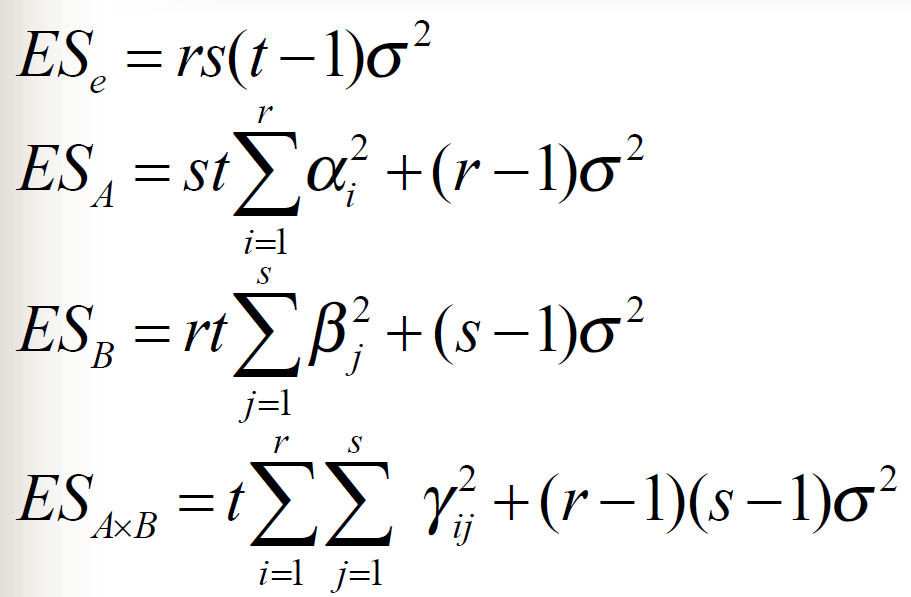


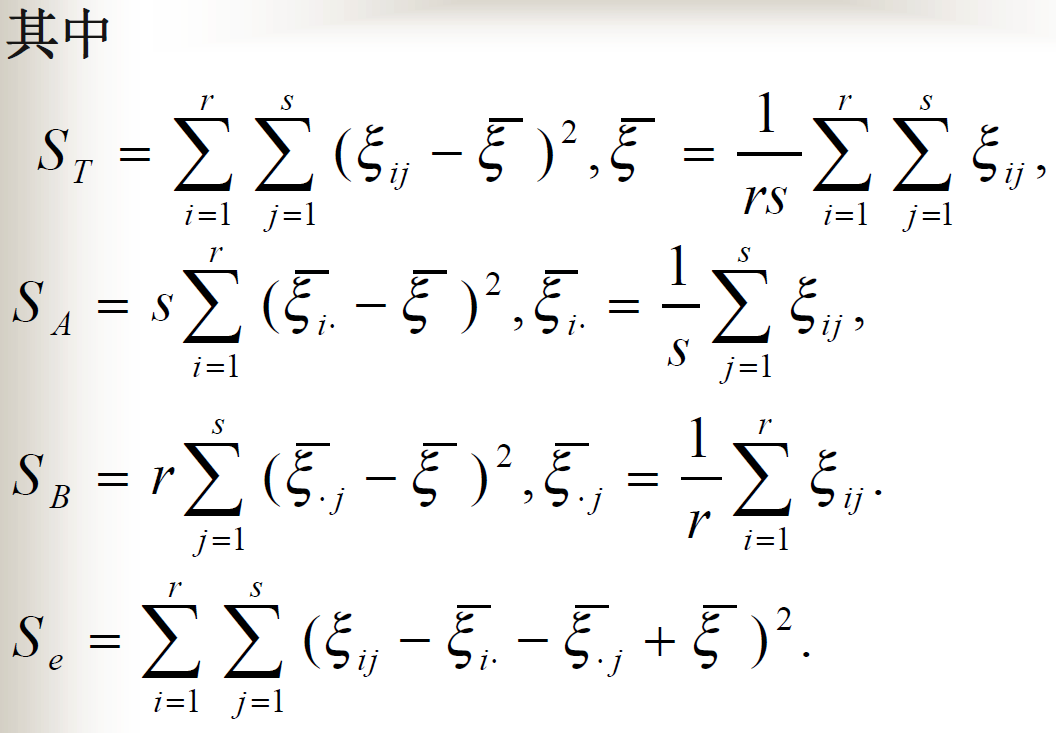




 浙公网安备 33010602011771号
浙公网安备 33010602011771号