D. Love-Hate

思路：

n的范围是比较大的，某个人不在答案中概率为1/2，我们考虑随机去选取50个人，那么这50个人都不在答案中的概率为\(1/2^{50}\),概率是十分小，那么也就是随机选取50次后，会有其中一些人是包含答案的一个较大子集。

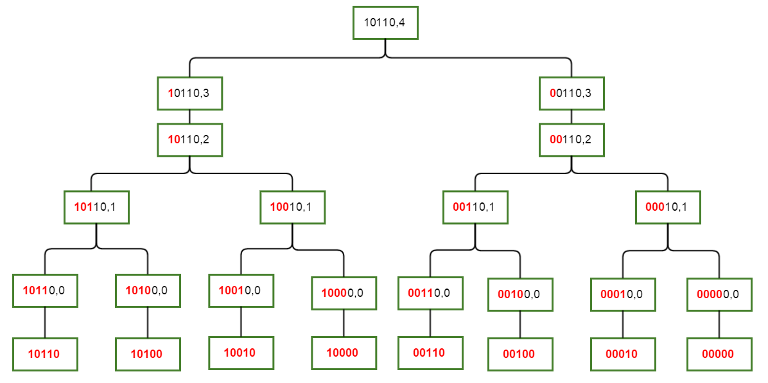
这里解释一下这道题定义的子集，比如1010有四个子集
分别为 1010 0101 1000 0100

即当前位为1的可变换为 1或 0， 如果当前位为0 ，则无需变换

我们随机选了一个人后，那我们考虑去枚举这个人所包含的子集，假如有k个1 那么就有\(2^k\)个子集，然后我们去看其他人对这些子集的包含程度如何，题目要求的是包含程度最高（即更多的1）

\(dp[i]=x\)表示有x个人的选项中包含 集合j

考虑如何进行dp：

假设随机被选中的人叫阿亮

dp初始化：

对于这n个人都有自己01串，

对于第i个人

我们要去找个一个最大的子集sum，sum满足既被阿亮包含又被 i 包含，那么这个子集sum需要加一，因为被他自己包含了

转移：

对于两个集合，1110 1100，我们不难得出，只要能够包含1110 那么必定也能够包含1100，因为后者的集合范围较小。

那我们考虑从大集合转移到小集合

vector bit 已经把随机选中的那个人的所有1的位置存了下来，最多也就15位

那么可以去枚举这些位置1的选择情况然后进行转移。

最终答案通过遍历所有的子集进行一个更新

（好像懵懵懂懂的，语言组织的不是很好，

codeforces上对sosdp的讲解：https://codeforces.com/blog/entry/45223

电音的视频讲解：https://www.bilibili.com/video/BV1L64y1R75n?spm_id_from=333.337.search-card.all.click

#include<bits/stdc++.h>
#define deb cout<<"--"<<endl;
#define int long long 
#define ll long long 
#define endl '\n'
using namespace std;
const int N=1e6+5;
const int inf=0x3f3f3f3f3f3f;
int a[N];
int n,m,p;
vector<int>bit,ans;
int dp[N];
void solve(){
    cin>>n>>m>>p;
    for(int i=1;i<=n;i++){
        string s;cin>>s;
        for(int j=0;j<m;j++){
            if(s[m-j-1]=='1'){
                a[i]+=(1ll<<j);
            }
        }
    }
    srand(time(0)*time(0));
    for(int k=1;k<=50;k++){
        int index=1ll*rand()*rand()%n+1;
        bit.clear();
        for(int j=0;j<m;j++){
            if((1ll<<j)&a[index]){
                bit.push_back(j);
            }
        }
        
        //dp的初始化
        memset(dp,0,sizeof(dp));
        for(int j=1;j<=n;j++){
            int sum=0;
            for(int i=0;i<bit.size();i++){
                if((1ll<<bit[i])&a[j]){
                    sum+=(1ll<<i);
                }
            }
            dp[sum]++;   //sum是a[j]的一个子集
        }
        //sosdp  
        
        for(int i=0;i<bit.size();i++){
            for(int j=0;j<=(1ll<<bit.size());j++){
                if((j&(1ll<<i))==0){
                    //这里==0的原因是，我们要转移到一个包含程度较小的，那也就是这一位为0，这个数1的位数越少，就会有更多·				
               	    //的人包含他
                    dp[j]+=dp[j+(1ll<<i)];
                }
            }
        }
        
        
        //去遍历所有可能的子集，看哪一个子集被更多的人包含，然后更新
        for(int i=0;i<(1<<15);i++){
            if(dp[i]>=(n+1)/2&&__builtin_popcount(i)>ans.size()){
                ans.clear();
                for(int j=0;j<m;j++){
                    if(i&(1ll<<j))ans.push_back(bit[j]);
                }
            }
        }
        
    }
    // cout<<ans.size()<<endl;
    string ens=string(m,'0');
        for(auto i:ans){
            ens[m-i-1]='1';
        }
        cout<<ens<<endl;
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); 
	int kase=1;
    // cin>>kase;
    for(int i=1;i<=kase;i++){solve();}
}