【弹簧阻尼器】无摩擦弹簧质量阻尼器系统稳态振动振幅比的三维曲面图研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

无摩擦弹簧质量阻尼器系统稳态振动振幅比的三维曲面图研究

一、研究背景与意义

无摩擦弹簧质量阻尼器系统是典型的单自由度振动系统，广泛应用于机械工程、土木工程和航空航天工程等领域。该系统由质量块、弹簧和阻尼器组成，在简谐激励下会产生稳态振动。振幅比（响应振幅与激励振幅的比值）是描述系统振动特性的重要参数。通过绘制振幅比的三维曲面图，可以直观展示不同频率比和阻尼比组合下的振幅比变化规律，为系统设计、振动控制和故障诊断提供理论依据。

二、系统模型与运动方程

系统构成：
- 质量块（m）：系统的惯性元件。
- 弹簧（k）：系统的弹性元件，提供恢复力。
- 阻尼器（c）：系统的耗能元件，提供阻尼力。
运动方程：
- 假定系统受到简谐外力 F(t)=F0cos(ωt) 的作用，其中 F0 是外力的幅值，ω 是外力的角频率。
- 根据牛顿第二定律，系统的运动方程为：mx¨+cx˙+kx=F0cos(ωt)。
- 其中，x 是质量块的位移，x˙ 和 x¨ 分别是位移对时间的一阶和二阶导数，代表速度和加速度。
稳态解：
- 系统的稳态解描述的是系统在长时间后的受迫振动，形式为 x(t)=Xcos(ωt−φ)，其中 X 是位移的幅值，φ 是相位角。
- 将特解代入运动方程，可以得到幅值 X 的表达式：X=(k−mω2)2+(cω)2F0。
振幅比：
- 振幅比 R 定义为响应振幅 X 与激励振幅 F0/k（静态位移）的比值：R=F0/kX=(1−r2)2+(2ζr)21。
- 其中，r=ω/ωn 为频率比，ωn=k/m 为系统的固有频率，ζ=c/(2mk) 为阻尼比。

三、三维曲面图绘制

数据准备：
- 定义频率比 r 的范围：r∈[0,3]。
- 定义阻尼比 ζ 的范围：ζ∈[0,1]。
- 对 r 和 ζ 进行均匀采样，生成网格点。
计算振幅比：
- 对每个网格点 (ri,ζj)，根据振幅比公式计算 Rij。
绘图工具选择：
- 使用 Python 的 Matplotlib 或 MATLAB 等工具绘制三维曲面图。

四、结果分析

共振现象：
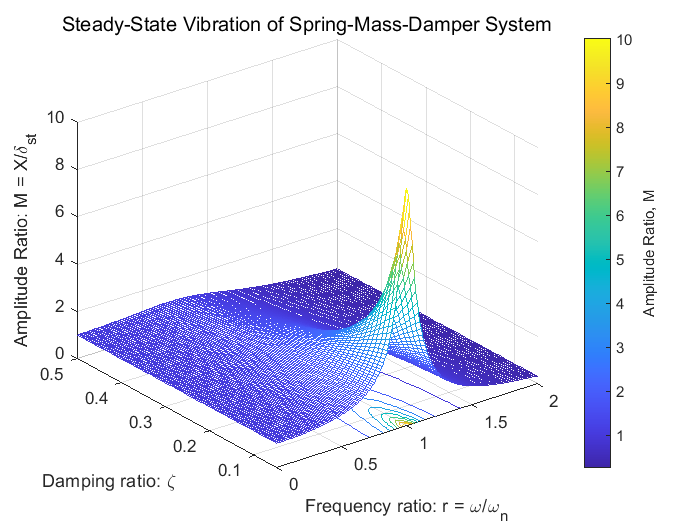
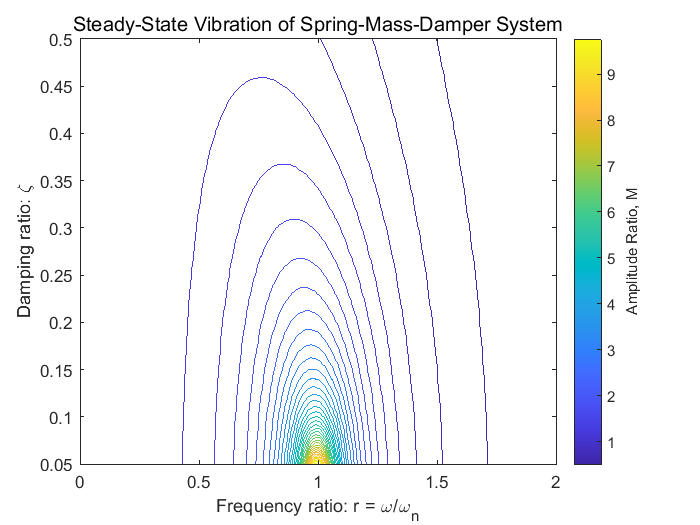
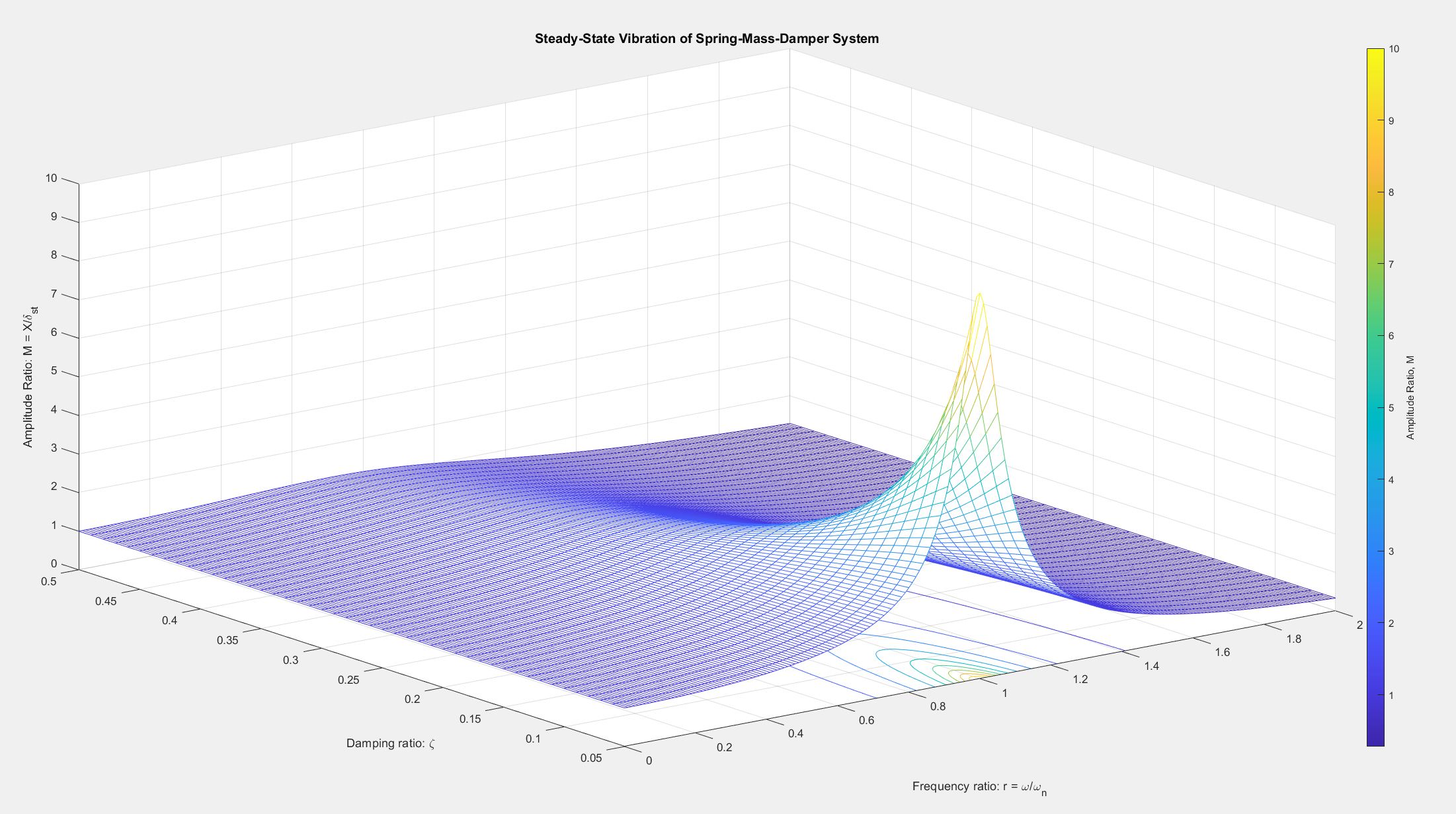
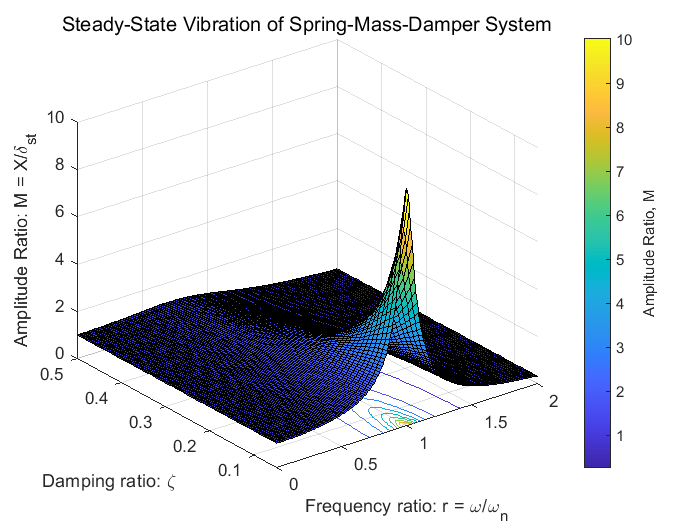
- 当 r≈1（共振区）且 ζ 较小时，振幅比出现峰值。
- 共振时的幅值取决于阻尼比 ζ 的大小。阻尼比越小，共振时的幅值越高。
阻尼比的影响：
- 增大阻尼比 ζ 可有效抑制共振峰值。
- 阻尼比增加时，共振峰降低，且峰值对应的频率略微偏离固有频率 ωn。
频率范围的影响：
- 远离共振区时，振幅比趋近于静态变形值（r≪1 时 R≈1）或趋于零（r≫1 时 R≈0）。
系统稳定性评估：
- 若某外力频率范围内振幅比过大，表明系统在该频率范围内容易发生共振，存在安全隐患。
- 通过分析三维曲面图，可以选择合适的材料和结构参数，避免系统工作在共振频率附近。

五、应用与展望

结构设计优化：
- 根据三维曲面图，优化阻尼器的设计，选择合适的阻尼系数，有效抑制振动，提高系统性能。
- 在汽车悬挂系统中，阻尼器的作用就是减少车身的振动，提高乘坐舒适性。
振动控制策略设计：
- 三维曲面图可作为振动控制策略设计的依据。通过施加主动或被动的振动控制措施，改变系统的频率响应特性，降低共振峰值，实现振动控制的目标。
- 例如，在桥梁设计中，可采用调谐质量阻尼器（TMD）来抑制桥梁的振动，提高桥梁的抗风稳定性。
故障诊断：
- 通过监测系统的振动频率和幅值，判断系统是否存在故障。例如，轴承损坏会导致系统产生异常振动，通过分析振动信号的频率成分和幅值大小，可以诊断轴承的故障类型和程度。
未来研究方向：
- 实际工程应用中需考虑更多复杂因素，如摩擦、非线性效应等。未来研究可进一步探索更复杂的振动系统，构建更精确的振动模型，开发更有效的振动控制策略。