暑期集训第十一天(7-2)题解及总结
小总结:
今天早上最先做的是先把昨天的那道恶心的树剖题调出来,直到吃完饭回来我才弄完-_- 。
之后我尝试着把ftp里面的对拍程序改成c++格式的(ftp里面的check.sh老师老师的时候不让下了),在考试之前五分钟终于成功了,一开考就兴奋的打了一遍(然鹅一上午并没有用QAQ)
T1:小猫爬山
这道题老师给出的答案竟然是暴搜???n<=18不应该是状压???看到这道题想到上周做过的一道名为"宝藏"的题目,那道题目之中我们用到一个循环来把一个二进制数字进行拆分,来进行预处理,这道题我们也可以用类似的思想来进行处理,先把不同状态的重量算一下,能装下就把这个dp赋值为1,否则为无穷大,之后对不同二进制数字进行拆分,进行拼接,求出最优解即可(之后看时间效率好像刚刚水过???)
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1<<20;
int w[50],trans[N],dp[N];
int lowbit(int x){
return x & -x;
}
int count(int x){
int cnt=1;
while(x){
if(x&1) return cnt;
x>>=1; cnt++;
}
return cnt;
}
int cal(int x){
int ans=0;
while(x){
int now=count(x);
ans+=w[now];
x-=lowbit(x);
}
return ans;
}
signed main(){
int n,m;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i) scanf("%lld",&w[i]);
int ed=(1<<n)-1;
memset(dp,0x3f,sizeof(dp));
for(int i=0;i<=ed;++i){
int now=cal(i);
if(now<=m) dp[i]=1;
}
for(int i=0;i<=ed;++i){
for(int j=i;j;j=(j-1)&i){
int k=i^j;
dp[i]=min(dp[i],dp[j]+dp[k]);
}
}
printf("%lld\n",dp[ed]);
return 0;
}
T2:猴腮雷
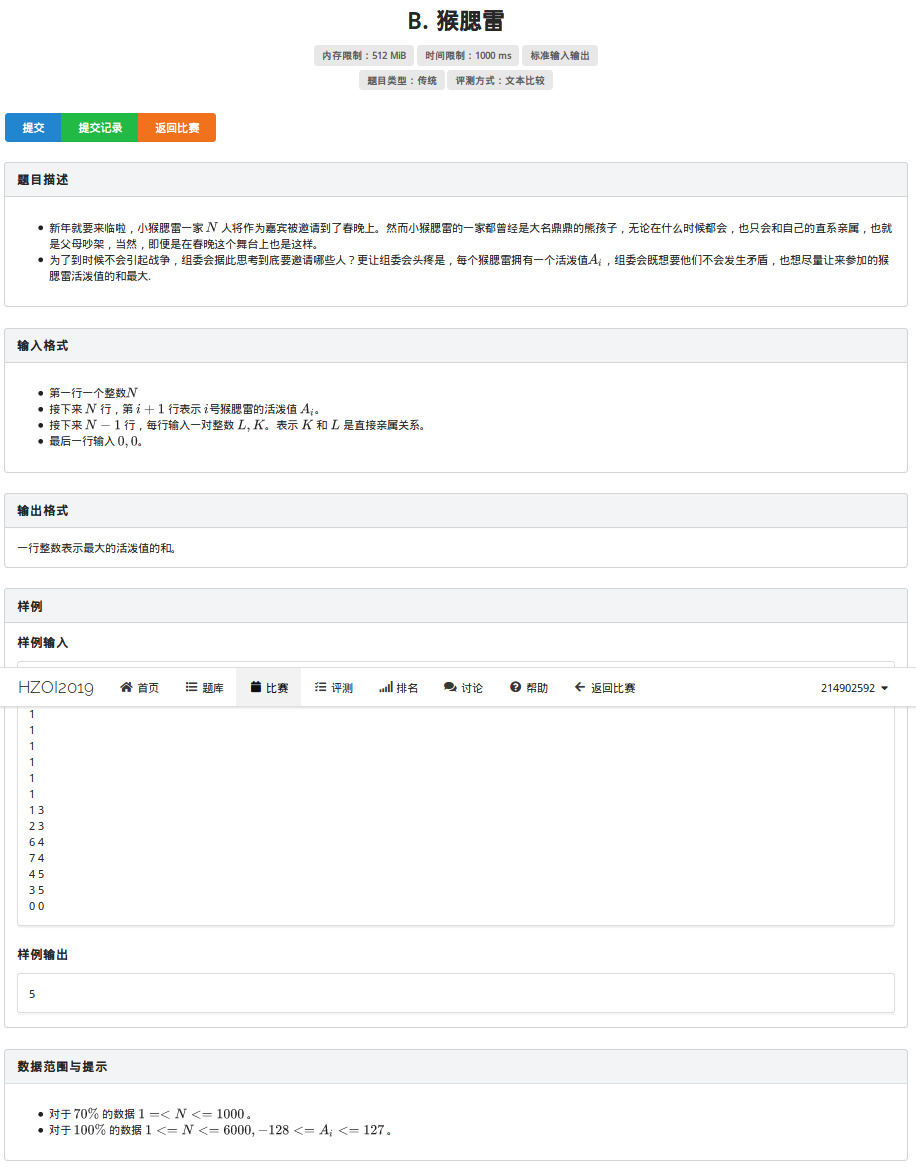
看到这个题目还以为这道题猴赛雷(很厉害),但是其实就是一个板子题,我们曾经做过一道题目叫做"没有上司的舞会",和这道题是一摸一样的,就是一个树归的板子,就不解释什么了.
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+10;
struct Node{
int next,to;
}edge[N];
int Head[N],tot,w[N];
void Add(int x,int y){
edge[++tot].to=y;
edge[tot].next=Head[x];
Head[x]=tot;
}
int dp[N][2];
void dfs(int u,int fa){
dp[u][1]+=w[u];
for(int i=Head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==fa) continue;
dfs(v,u);
dp[u][1]+=dp[v][0];
dp[u][0]+=max(dp[v][1],dp[v][0]);
}
}
signed main(){
int n;
scanf("%lld",&n);
for(int i=1;i<=n;++i) scanf("%lld",&w[i]);
int x,y;
while(scanf("%lld%lld",&x,&y)==2&&x&&y){
Add(x,y);Add(y,x);
}
dfs(1,1);
printf("%lld\n",max(dp[1][0],dp[1][1]));
return 0;
}
T3:小烈送菜
看到这道题之后先想了半个小时,又想了十五分钟,默默的看了一下表,默默的看了一下数据范围,之后去打了一个30pts的暴力....
这道题的思维还是挺清奇的,我们想到小烈一个来回一定会把所有的人都送到,我们的价值和就是相邻的分数的乘积,这好像和顺序没有任何关系???于是我们可以把小烈的返回的方向反转,换为两个人从起点向终点进行行走,两个人扫过的范围必须满足所有的人都被送到,于是考虑dp[i][j]表示第一个人在i,另一个在j的情况,由于i,j可以互换,于是有f[i][j]==f[j][i],这样我们就可以始终假设i>j,我们的下一状态dp[i+1][j]可以从i和j两个地方进行转移,但是如果从j转移,另一个人此时一定在i点,于是存在转移:f[i+1][j]=max(f[i+1][j],f[i][j]+a[i]∗a[i+1]),f[i+1][i]=max(f[i+1][i],f[i][j]+a[j]∗a[i+1])
之后就解决了.
#include<bits/stdc++.h>
using namespace std;
const int N=2505;
int a[N],dp[N][N],ans=0;
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i)
for(int j=0;j<i;++j){
dp[i+1][j]=max(dp[i+1][j],dp[i][j]+a[i]*a[i+1]);
dp[i+1][i]=max(dp[i+1][i],dp[i][j]+a[j]*a[i+1]);
}
for(int i=0;i<n;++i)
ans=max(ans,dp[n][i]+a[n]*a[i]);
printf("%d\n",ans);
return 0;
}
推老师博客++:https://www.cnblogs.com/hbhszxyb/p/13223698.html
T4:Siano
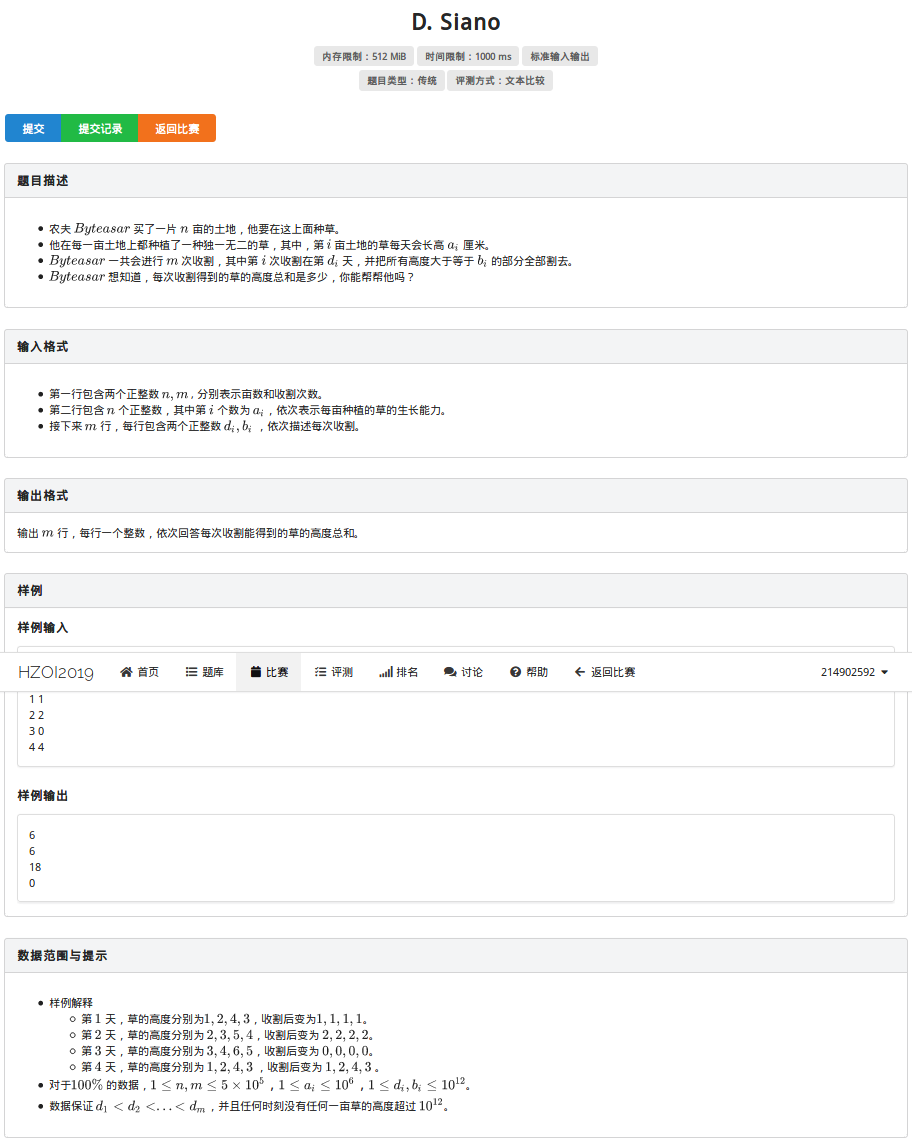
(为什么线段树都这么难调呀QAQ)
我们不难发现草的高度无论何时都具有单调性,长得高的永远高,于是我们考虑排序后用线段数来进行维护区间长度,并用二分来进行查询左边界,但是这样的时间效率是n*log^2的,只能拿到六十分,于是考虑如何去掉二分的过程,我们可以维护一个区间的最大值,(其实就是右儿子的大小,右面永远比左边大),之后进行从右边到左的查询,直到遇到一个小于修改值的,这样我们就可以砍掉一个log,成功晋级为nlogn的时间效率,这样就不会超时啦,但是这道题的代码不怎么好调,最初只有100行,让我调完后就成了150行???其实后来发现我的方法繁琐了,其实是不用单独的修改操作的,这里放一个大佬的代码吧.

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define ll long long 5 using namespace std; 6 const int N=5e5+10; 7 struct Tree{ 8 int l,r; 9 ll sum,tar,tard,a,last,Mx,Mi; 10 }T[N<<2]; 11 int a[N]; 12 #define ls rt<<1 13 #define rs rt<<1|1 14 void Build(int rt,int l,int r){ 15 T[rt].l=l;T[rt].r=r;T[rt].tar=-1; 16 if(l==r){ 17 T[rt].a=a[l]; 18 return ; 19 } 20 int mid=l+r>>1; 21 Build(ls,l,mid); 22 Build(rs,mid+1,r); 23 T[rt].a=T[ls].a+T[rs].a; 24 } 25 void pushdown(int rt){ 26 if(T[rt].tar==-1)return; 27 T[ls].sum=T[rt].tar*(T[ls].r-T[ls].l+1); 28 T[rs].sum=T[rt].tar*(T[rs].r-T[rs].l+1); 29 T[ls].tar=T[rs].tar=T[ls].Mx=T[ls].Mi=T[rs].Mx=T[rs].Mi=T[rt].tar; 30 T[ls].tard=T[rs].tard=T[ls].last=T[rs].last=T[rt].tard; 31 T[rt].tar=-1; 32 } 33 ll query(int rt,ll d,ll b){ 34 T[rt].sum+=T[rt].a*(d-T[rt].last); 35 T[rt].Mx+=a[T[rt].r]*(d-T[rt].last); 36 T[rt].Mi+=a[T[rt].l]*(d-T[rt].last); 37 T[rt].last=d; 38 ll ans=0; 39 if(T[rt].Mx<=b)return 0; 40 if(T[rt].Mi>b){ 41 ans+=T[rt].sum-b*(T[rt].r-T[rt].l+1); 42 T[rt].tard=T[rt].last=d; 43 T[rt].tar=b; 44 T[rt].sum=b*(T[rt].r-T[rt].l+1); 45 T[rt].Mx=T[rt].Mi=b; 46 return ans; 47 } 48 pushdown(rt); 49 ans=query(ls,d,b)+query(rs,d,b); 50 T[rt].sum=T[ls].sum+T[rs].sum; 51 T[rt].Mi=T[ls].Mi;T[rt].Mx=T[rs].Mx; 52 return ans; 53 } 54 int main(){ 55 int n,m; 56 scanf("%d%d",&n,&m); 57 for(int i=1;i<=n;i++)scanf("%d",&a[i]); 58 sort(a+1,a+n+1); 59 Build(1,1,n); 60 for(int i=1;i<=m;i++){ 61 ll d,b; 62 scanf("%lld%lld",&d,&b); 63 printf("%lld\n",query(1,d,b)); 64 } 65 }
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lson (t<<1)
#define rson (t<<1|1)
#define mid ((l+r)>>1)
const int N=5e6+10;
int w[N];
int n,m,Max=0,Min=0;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
struct Tree{
int cnt,w,siz,lazycnt,lazygai,grow,Max,maxgrow;
}tree[N];
void pushup(int t){
tree[t].w=tree[lson].w+tree[rson].w;
tree[t].Max=tree[rson].Max;
tree[t].maxgrow=tree[rson].maxgrow;
}
void build(int t,int l,int r){
tree[t].siz=r-l+1;
tree[t].lazygai=-1;
if(l==r){
tree[t].grow=tree[t].maxgrow=w[l];
return;
}
build(lson,l,mid);build(rson,mid+1,r);
tree[t].grow=tree[lson].grow+tree[rson].grow;
pushup(t);
}
void pushdown1(int t){
if(!tree[t].lazycnt) return;
tree[lson].lazycnt+=tree[t].lazycnt;
tree[rson].lazycnt+=tree[t].lazycnt;
tree[lson].w+=tree[t].lazycnt*tree[lson].grow;
tree[rson].w+=tree[t].lazycnt*tree[rson].grow;
tree[lson].Max+=tree[lson].maxgrow*tree[t].lazycnt;
tree[rson].Max+=tree[rson].maxgrow*tree[t].lazycnt;
tree[t].lazycnt=0;
}
void pushdown2(int t){
if(tree[t].lazygai==-1) return;
tree[lson].lazycnt=tree[rson].lazycnt=0;
tree[lson].lazygai=tree[rson].lazygai=tree[t].lazygai;
tree[lson].Max=tree[t].lazygai;
tree[rson].Max=tree[t].lazygai;
tree[lson].w=tree[t].lazygai*tree[lson].siz;
tree[rson].w=tree[t].lazygai*tree[rson].siz;
tree[t].lazygai=-1;
}
void Add(int t,int l,int r,int al,int ar,int num){
if(al<=l&&r<=ar){
tree[t].lazycnt+=num;
tree[t].w+=num*tree[t].grow;
tree[t].Max+=tree[t].maxgrow*num;
return;
}
pushdown2(t);
pushdown1(t);
if(ar<=mid) Add(lson,l,mid,al,ar,num);
else if(al>mid) Add(rson,mid+1,r,al,ar,num);
else{
Add(lson,l,mid,al,ar,num);Add(rson,mid+1,r,al,ar,num);
}
pushup(t);
}
int search_(int t,int l,int r,int val){
if(l==r)
return tree[t].Max>=val?l:(n+1);
pushdown2(t);pushdown1(t);
if(tree[lson].Max<val)
return search_(rson,mid+1,r,val);
return search_(lson,l,mid,val);
}
void change(int t,int l,int r,int cl,int cr,int num){
if(cl<=l&&r<=cr){
tree[t].lazygai=num;
tree[t].lazycnt=0;
tree[t].w=num*tree[t].siz;
tree[t].Max=num;
return;
}
pushdown2(t);
pushdown1(t);
if(tree[t].lazygai) pushdown2(t);
if(cr<=mid) change(lson,l,mid,cl,cr,num);
else if(cl>mid) change(rson,mid+1,r,cl,cr,num);
else{
change(lson,l,mid,cl,cr,num);change(rson,mid+1,r,cl,cr,num);
}
pushup(t);
}
int query(int t,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr){
return tree[t].w;
}
pushdown2(t);
pushdown1(t);
if(qr<=mid) return query(lson,l,mid,ql,qr);
else if(ql>mid) return query(rson,mid+1,r,ql,qr);
else{
return query(lson,l,mid,ql,qr)+query(rson,mid+1,r,ql,qr);
}
}
int erfen(int l,int r,int num){
while(l<r){
int now=query(1,1,n,mid,mid);
if(now<=num) l=mid+1;
else r=mid;
}
return r;
}
int pre=0;
signed main(){
n=read();m=read();
for(int i=1;i<=n;++i) w[i]=read();
sort(w+1,w+1+n);
build(1,1,n);
for(int i=1;i<=m;++i){
int x,y;
x=read();y=read();
Add(1,1,n,1,n,x-pre);
pre=x;
int now=search_(1,1,n,y);
if(now==n+1){
printf("0\n");continue;
}
int ans=query(1,1,n,now,n)-(n-now+1)*y;
if(ans>0)
printf("%lld\n",query(1,1,n,now,n)-(n-now+1)*y);
else{
printf("0\n");continue;
}
change(1,1,n,now,n,y);
}
return 0;
}
总结:
今天我怎么感觉调了一天的代码QAQ上午调昨天的树剖,以及考试时的线段树,下午一下午就把第四道题调过了,晚上就复习了一点数论的内容,看来代码能力还是有待提高,明天我们不考试,自己可以去尝试着盲打几道线段树,单调队列,树剖的板子题,至少以后不能再在这上面花费大量的时间了,最后,希望明天自己能有一个高的效率吧.





 浙公网安备 33010602011771号
浙公网安备 33010602011771号