暑期集训第十天(7-1)题解及总结
小总结:
昨天调一道树剖的题人都弄傻了,所以就没有写题解(我们调这一道题的表示都很恶心),今天一起补上吧,还有几天就要高考了,我们也准备搬着主机挪到国际部了,今天老师们都去调网络了,一下午只有我们在机房里面颓......
T1:最大公约数和最小公倍数问题
emm...这道题直接写暴力都能水几十分,但是虎哥给出的正解比暴力要快一些,就是统计出两数除最大公因数之外的质数因子,统计好后直接算2的次方即可.
#include<bits/stdc++.h>
using namespace std;
#define int long long
int prime[50050000],vis[5005000],tot,ca[500500],cb[500500];
signed main(){
//freopen("a.in","r",stdin);
//freopen("a.out","w",stdout);
int x,y;
scanf("%lld%lld",&x,&y);
if(x==y){
printf("1\n");
return 0;
}
for(int i=2;i<=y;++i){
if(!vis[i]){
vis[i]=i;
prime[++tot]=i;
}
for(int j=1;j<=tot&&i*prime[j];++j){
if(prime[j]>vis[i]||prime[j]>y/i) break;
vis[i*prime[j]]=prime[j];
}
}
int flag=0;
int s1=0,s2=0;
for(int i=1;i<=tot&&prime[i]<=x;++i){
while(x%prime[i]==0){
x/=prime[i];
++ca[prime[i]];
if(ca[prime[i]]==1) ++s1;
}
}
int cnt=0;
for(int i=1;i<=tot&&prime[i]<=y;++i){
while(y%prime[i]==0){
y/=prime[i];
++cb[prime[i]];
if(cb[prime[i]]==1) ++s2;
}
if(ca[prime[i]]>0&&ca[prime[i]]<=cb[prime[i]]) {
++flag;
if(cb[prime[i]]>ca[prime[i]]) ++cnt;
}
}
if(flag!=s1) printf("0\n");
else{
if(cnt==0) printf("%lld\n",(int)1<<(s2-s1));
else printf("%lld\n",(int)1<<(s2-s1+cnt));
}
return 0;
}
T2:方格取数
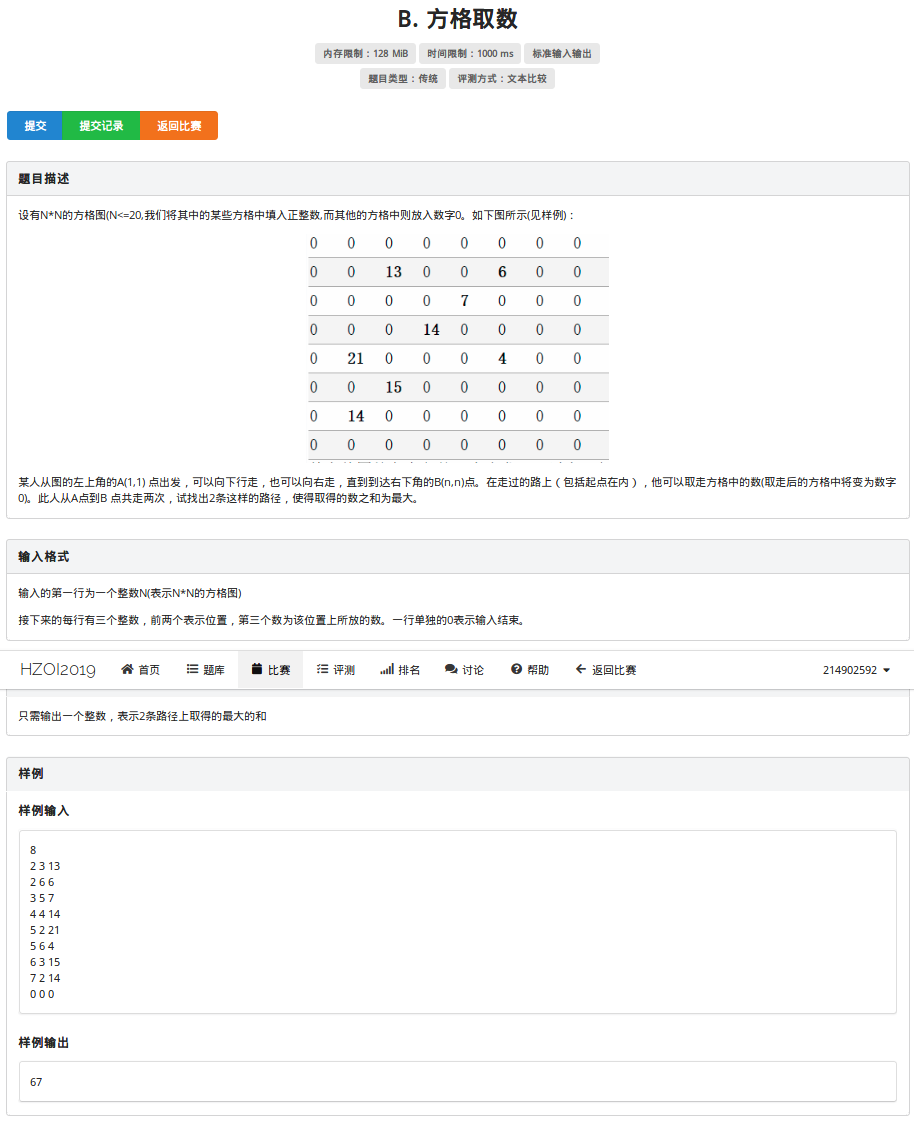
这道题我当时的想法就是先跑一边二维的dp,记录路径后清空,之后再跑一边,将两次dp所得的答案进行加和即可.但是这是贪心,很明显是错误的,于是考虑数组开上4维,分别表示第一次的位置和第二次的位置,转移的时候判断两人是否走到了一起,在一起则加一次得分,否则两个点位置都加.最后输出终点得分即可.
#include<bits/stdc++.h>
//#define debug printf("-debug-\n")
using namespace std;
int dp[100][100][100][100],a[500][500];
signed main(){
//freopen("a.in","r",stdin);
//freopen("a.out","w",stdout);
int n;
scanf("%d",&n);
int x,y,z;
while(scanf("%d%d%d",&x,&y,&z)==3&&x&&y&&z){
a[x][y]=z;
}
//debug;
for(int i=1;i<=n;++i){
//debug;
for(int j=1;j<=n;++j)
for(int k=1;k<=n;++k)
for(int p=1;p<=n;++p){
//debug;
if(i==k && j==p){
dp[i][j][k][p]=max(dp[i][j][k][p],max(dp[i-1][j][k-1][p],dp[i-1][j][k][p-1])+a[k][p]);
dp[i][j][k][p]=max(dp[i][j][k][p],max(dp[i][j-1][k-1][p],dp[i][j-1][k][p-1])+a[k][p]);
}
else{
dp[i][j][k][p]=max(dp[i][j][k][p],max(dp[i-1][j][k-1][p],dp[i-1][j][k][p-1])+a[i][j]+a[k][p]);
dp[i][j][k][p]=max(dp[i][j][k][p],max(dp[i][j-1][k-1][p],dp[i][j-1][k][p-1])+a[i][j]+a[k][p]);
}
}
}
printf("%d\n",dp[n][n][n][n]);
return 0;
}
T3: WYT的刷子

这道题在这次考试之中算是比较难的一道题了(本来做出来了,没开longlong黑掉了我60pts >_<) ,老师讲课的时候用到的是优先队列,而我对这个东西不怎么熟悉,所以考试的时候用到的是线段树,建两个线段树,分别维护区间最大值和刷到的最小值,代码的核心在这一行:
if(Min1<=pre&&Min1<=Min2&&i<r+1&&j!=n) continue;
这行代码用来去除掉不用刷的情况,Min1表示当前刷到的最小值,Min2表示下一位刷到的最小值,pre表示上一次刷得到的最小值,r表示上一次刷到的右边界,如果当前刷到的高度比前一次和下一次都要低,我们尽可能的不在这里刷,除了它的左边界大到再不刷就出现断层或是到了最友端,最后统计答案即可.
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lson (t<<1)
#define rson (t<<1|1)
#define mid ((l+r)>>1)
int a[5000500];
int Pow(int x,int y){
int ans=1;
while(y){
if(y&1) ans*=x;
y>>=1;
x=x*x;
}
return ans;
}
int tree[6005000],tre[6005000],lazy[6005000];
void pushup(int t){
tree[t]=min(tree[lson],tree[rson]);
}
void pushdown(int t,int l,int r){
tre[lson]=max(tre[lson],lazy[t]);
tre[rson]=max(tre[rson],lazy[t]);
lazy[lson]=max(lazy[lson],lazy[t]);
lazy[rson]=max(lazy[rson],lazy[t]);
}
void build(int t,int l,int r){
if(l==r){
tree[t]=a[l];
return;
}
build(lson,l,mid);build(rson,mid+1,r);
pushup(t);
}
int query(int t,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr){
return tree[t];
}
if(qr<=mid) query(lson,l,mid,ql,qr);
else if(ql>mid) query(rson,mid+1,r,ql,qr);
else{
return min(query(lson,l,mid,ql,qr),query(rson,mid+1,r,ql,qr));
}
}
void change(int t,int l,int r,int cl,int cr,int num){
if(cl<=l&&r<=cr){
tre[t]=max(tre[t],num);
lazy[t]=max(lazy[t],num);
//printf("=%d %d %d\n",l,r,tre[t]);
return;
}
pushdown(t,l,r);
if(cr<=mid) change(lson,l,mid,cl,cr,num);
else if(cl>mid) change(rson,mid+1,r,cl,cr,num);
else{
change(lson,l,mid,cl,cr,num);change(rson,mid+1,r,cl,cr,num);
}
tre[t]=max(tre[lson],tre[rson]);
//printf("%d %d %d\n",l,r,tre[t]);
}
int quer(int t,int l,int r,int q){
if(l==r){
//printf("=%d %d\n",l,tre[t]);
return tre[t];
}
pushdown(t,l,r);
if(q<=mid) return quer(lson,l,mid,q);
else return quer(rson,mid+1,r,q);
}
int b[5000500],pre=0,r,ans1,c[5000500];
signed main(){
//freopen("a.in","r",stdin);
//freopen("a.out","w",stdout);
int n,m;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i){
scanf("%lld",&a[i]);
}
build(1,1,n);
int cnt=0;
r=0;
for(int i=1,j;(j=i+m-1)<=n;++i){
int Min1=query(1,1,n,i,j);
int Min2=query(1,1,n,i+1,j+1);
if(Min1<=pre&&Min1<=Min2&&i<r+1&&j!=n) continue;
change(1,1,n,i,j,Min1);
pre=Min1;r=j;
cnt++;
}
for(int i=1;i<=n;++i){
ans1+=a[i]-quer(1,1,n,i);
//printf("=%d\n",quer(1,1,n,i));
}
printf("%lld\n%lld\n",ans1,cnt);
return 0;
}
T4:2017种树
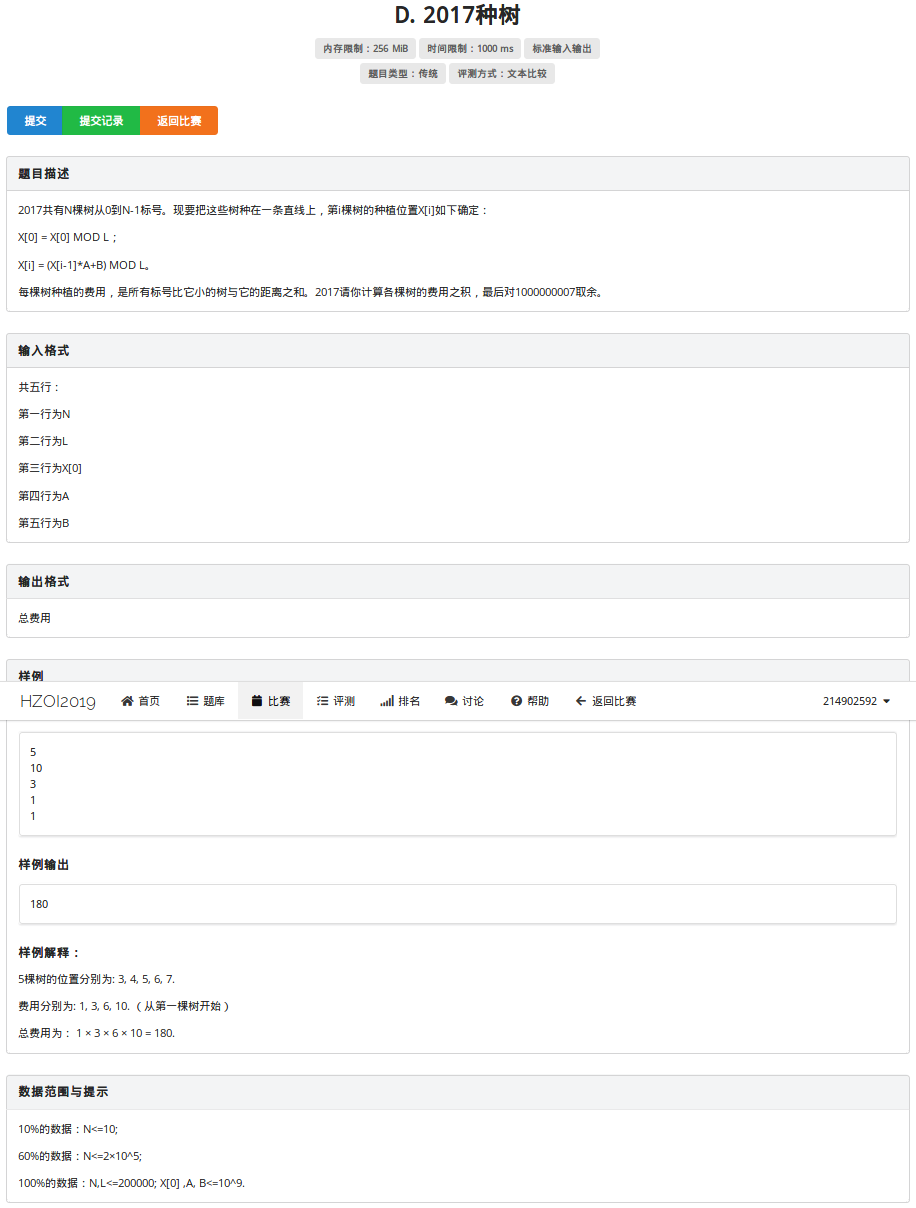
这道题的代码不怎么好调(写第三题的线段树把时间用光了),这道题首先不能读错题目,由于取模的存在,一颗树可能在他之前的树的位置之前,我们容易知道一棵树的花费就是前面点的个数乘上当前的点的坐标减去之前的点的坐标和(注意绝对值),我们可以维护一颗线段树,表示在当前位置的树的个数和坐标和,之后拿当前点的坐标减去前面点的坐标,再拿后面点的坐标和减去当前点的坐标就可以了.
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define debug printf("-debug-\n")
#define lson (t<<1)
#define rson (t<<1|1)
#define mid ((l+r)>>1)
const int M=1000000007;
const int N=1e6+10;
struct Tree{
int w,cnt;
}tree[N];
int n,Mod,x[500500],a,b,ans=1,pre;
void pushup(int t){
tree[t].w=(tree[lson].w+tree[rson].w)%M;
tree[t].cnt=(tree[lson].cnt+tree[rson].cnt)%M;
}
void change(int t,int l,int r,int pos){
if(l==r){
tree[t].cnt=(tree[t].cnt+1)%M;
tree[t].w=(tree[t].w+pos)%M;
return;
}
if(pos<=mid) change(lson,l,mid,pos);
else change(rson,mid+1,r,pos);
pushup(t);
}
int queryw(int t,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr){
return tree[t].w%M;
}
if(qr<=mid) return queryw(lson,l,mid,ql,qr)%M;
else if(ql>mid) return queryw(rson,mid+1,r,ql,qr)%M;
else return (queryw(lson,l,mid,ql,qr)+queryw(rson,mid+1,r,ql,qr))%M;
}
int querycnt(int t,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr){
return tree[t].cnt%M;
}
if(qr<=mid) return querycnt(lson,l,mid,ql,qr)%M;
else if(ql>mid) return querycnt(rson,mid+1,r,ql,qr)%M;
else return (querycnt(lson,l,mid,ql,qr)+querycnt(rson,mid+1,r,ql,qr))%M;
}
signed main(){
scanf("%lld%lld%lld%lld%lld",&n,&Mod,&x[0],&a,&b);
x[0]%=Mod;
for(int i=1;i<n;++i){
x[i]=(x[i-1]*a+b)%Mod;
}
change(1,0,Mod-1,x[0]);
for(int i=1;i<n;++i){
int a,b,now=0;
a=querycnt(1,0,Mod-1,0,x[i]);
b=queryw(1,0,Mod-1,0,x[i]);
now=(now+a*x[i])%M;
now=(now-b)%M;
a=querycnt(1,0,Mod-1,x[i],Mod-1);
b=queryw(1,0,Mod-1,x[i],Mod-1);
now=(now+b)%M;
now=(now-a*x[i]+M)%M;
ans=ans*now%M;
change(1,0,Mod-1,x[i]);
}
printf("%lld\n",ans);
return 0;
}
一道莫名恶心难调的树剖题目:P4315 月下“毛景树”
题目链接:https://www.luogu.com.cn/problem/P4315
这道题和其他普通树剖的区别就是这个树只有边权而没有点权,但是我们可以考虑把这个点与其父亲结点之间边的边权转化为这个点的点权,之后就可以愉快的树剖了,但是注意由于不包括父亲节点,查询的时候左端点的编号要加一(调试真恶心).
#include<bits/stdc++.h>
using namespace std;
const int maxn=4e6+5;
struct asd{
int from,to,next,val;
}b[maxn];
int head[maxn],tot=1;
void ad(int aa,int bb,int cc){
b[tot].from=aa;
b[tot].to=bb;
b[tot].val=cc;
b[tot].next=head[aa];
head[aa]=tot++;
}
int dep[maxn],sizz[maxn],son[maxn],f[maxn];
int uu[maxn],vv[maxn],ww[maxn];
void dfs(int now,int fa){
sizz[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(u==fa) continue;
dep[u]=dep[now]+1;
f[u]=now;
dfs(u,now);
sizz[now]+=sizz[u];
if(son[now]==0 || sizz[son[now]]<sizz[u]){
son[now]=u;
}
}
}
int dfn[maxn],rk[maxn],a[maxn],tp[maxn],cnt;
void dfs2(int now,int top){
dfn[now]=++cnt;
rk[cnt]=a[now];
tp[now]=top;
if(son[now]) dfs2(son[now],top);
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(u==f[now] || u==son[now]) continue;
dfs2(u,u);
}
}
struct trr{
int l,r,siz,laz,w,tag;
}tr[maxn];
void push_up(int da){
tr[da].w=max(tr[da<<1].w,tr[da<<1|1].w);
}
void push_down(int da){
if(tr[da].laz>=0){
tr[da<<1].tag=tr[da<<1|1].tag=0;
tr[da<<1].w=tr[da<<1].laz=tr[da<<1|1].w=tr[da<<1|1].laz=tr[da].laz;
tr[da].laz=-1;
}
if(tr[da].tag){
tr[da<<1].tag+=tr[da].tag;
tr[da<<1|1].tag+=tr[da].tag;
tr[da<<1].w+=tr[da].tag;
tr[da<<1|1].w+=tr[da].tag;
tr[da].tag=0;
}
}
void build(int da,int l,int r){
tr[da].l=l,tr[da].r=r,tr[da].siz=r-l+1,tr[da].laz=-1;
if(l==r){
tr[da].w=rk[l];
return;
}
int mids=(l+r)>>1;
build(da<<1,l,mids);
build(da<<1|1,mids+1,r);
push_up(da);
}
void xg(int da,int l,int r,int w){
if(tr[da].l>=l && tr[da].r<=r){
tr[da].w=w;
tr[da].tag=0;
tr[da].laz=w;
return;
}
push_down(da);
int mids=(tr[da].l+tr[da].r)>>1;
if(l<=mids) xg(da<<1,l,r,w);
if(r>mids) xg(da<<1|1,l,r,w);
push_up(da);
}
void add(int da,int l,int r,int w){
if(tr[da].l>=l && tr[da].r<=r){
tr[da].w+=w;
tr[da].tag+=w;
return;
}
push_down(da);
int mids=(tr[da].l+tr[da].r)>>1;
if(l<=mids) add(da<<1,l,r,w);
if(r>mids) add(da<<1|1,l,r,w);
push_up(da);
}
int cx(int da,int l,int r){
if(tr[da].l>=l && tr[da].r<=r){
return tr[da].w;
}
push_down(da);
int mids=(tr[da].l+tr[da].r)>>1;
int ans=0;
if(l<=mids) ans=max(ans,cx(da<<1,l,r));
if(r>mids) ans=max(ans,cx(da<<1|1,l,r));
return ans;
}
void trxg(int u,int v,int w){
while(tp[u]!=tp[v]){
if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
xg(1,dfn[tp[u]],dfn[u],w);
u=f[tp[u]];
}
if(dep[u]<dep[v]) swap(u,v);
//printf("%d %d\n",dfn[v]+1,dfn[u]);
if(dfn[v]<dfn[u]) xg(1,dfn[v]+1,dfn[u],w);
}
void trad(int u,int v,int w){
while(tp[u]!=tp[v]){
if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
add(1,dfn[tp[u]],dfn[u],w);
u=f[tp[u]];
}
if(dep[u]<dep[v]) swap(u,v);
//printf("%d %d\n",dfn[v]+1,dfn[u]);
if(dfn[v]<dfn[u]) add(1,dfn[v]+1,dfn[u],w);
}
int trcx(int u,int v){
int ans=0;
while(tp[u]!=tp[v]){
if(dep[tp[u]]<dep[tp[v]]) swap(u,v);
//printf("%d %d\n",dfn[tp[u]],dfn[u]);
ans=max(ans,cx(1,dfn[tp[u]],dfn[u]));
u=f[tp[u]];
}
if(dep[u]<dep[v]) swap(u,v);
if(dfn[v]<dfn[u]) ans=max(ans,cx(1,dfn[v]+1,dfn[u]));
return ans;
}
int main(){
/*freopen("P4315_1.in","r",stdin);
freopen("my.out","w",stdout);*/
memset(head,-1,sizeof(head));
int n;
scanf("%d",&n);
for(int i=1;i<n;i++){
int aa,bb,cc;
scanf("%d%d%d",&aa,&bb,&cc);
ad(aa,bb,cc);
ad(bb,aa,cc);
uu[i]=aa;
vv[i]=bb;
ww[i]=cc;
}
dep[1]=1;
dfs(1,0);
for(int i=1;i<n;i++){
int aa=uu[i],bb=vv[i],cc=ww[i];
if(dep[aa]<dep[bb]) a[bb]=cc;
else a[aa]=cc;
}
dfs2(1,1);
build(1,1,n);
char s[10];
while(scanf("%s",s)!=EOF && s[0]!='S'){
if(s[0]=='M'){
int aa,bb;
scanf("%d%d",&aa,&bb);
printf("%d\n",trcx(aa,bb));
} else if(s[0]=='A'){
int aa,bb,cc;
scanf("%d%d%d",&aa,&bb,&cc);
trad(aa,bb,cc);
} else if(s[0]=='C' && s[1]=='o'){
int aa,bb,cc;
scanf("%d%d%d",&aa,&bb,&cc);
trxg(aa,bb,cc);
} else {
int aa,bb;
scanf("%d%d",&aa,&bb);
trxg(uu[aa],vv[aa],bb);
}
}
return 0;
}
总结:
其实这篇题解是7月2号补的,昨天调上面那道题调了一晚上......昨天成绩有所下滑,已经将近掉出了前十了,说明自己在代码准确性和读题上还存有问题(开longlong),在之后的练习之中还要进行注意,另外今天和liuchang尝试了进行gdb学习(感觉还不如我在代码中输出中间变量好用),在以后应该可以派上用场,最后,一如既往的,希望明天(7月3日)会更好.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号