离散化

1. 城市正视图

来源：《算法竞赛入门经典》
原题链接

题目描述

给定\(n\)坐房子的左下角坐标\(x\), \(y\), 还有宽度\(w\)(\(x\)方向的长度), 深度\(d\)(\(y\)方向的长度), 高度\(h\)(\(z\)方向的长度). 输出正视图中能看到的所有建筑物, 按照左下角x坐标从小到大进行排序, 左下角x坐标相同时, 按y坐标从小到大排序.

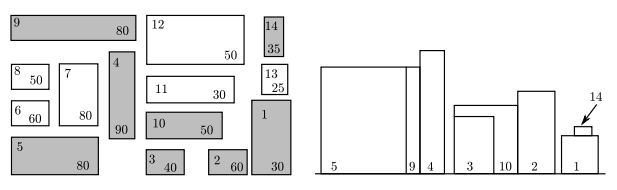
输入格式

有若干组测试样例.

对于每一组测试样例, 第一行为建筑物的个数\(n\).

接下来\(n\)行中的每一行输入四个数据, 分别代表编号为\(1\)~\(n\)的建筑物对应的\(x\)坐标, \(y\)坐标, 宽度\(w\), 深度\(d\), 高度\(h\).

输出格式

对于第\(k\)组测试样例.

第一行输出For map #k, the visible buildings are numbered as follows:

第二行输出符合题意的建筑物的编号,中间用空格隔开.

注意: 不同测试样例之间输出空行.

数据范围

\(n \le 100\)

输入样例

14
160 0 30 60 30
125 0 32 28 60
95 0 27 28 40
70 35 19 55 90
0 0 60 35 80
0 40 29 20 60
35 40 25 45 80
0 67 25 20 50
0 92 90 20 80
95 38 55 12 50
95 60 60 13 30
95 80 45 25 50
165 65 15 15 25
165 85 10 15 35
0

输出样例

For map #1, the visible buildings are numbered as follows:
5 9 4 3 10 2 1 14

---

算法：（离散化）\(O(n)\)

算法内容

• 由于深度并不会影响建筑物从南向北的可见性, 所以可以忽略深度.

• 朴素思想: 我们用结构体存下所有的建筑物, 从小到大枚举所有的建筑物, 对于每一个建筑物\(i\),枚举所有的\(x\), 判断\(i\)在\(x\)中是否可见.

• 朴素做法行不通是由于\(x\)是实数, 有无穷多个, 并且一个建筑物可能只有部分可见,无法枚举所有\(x\)坐标, 所以可以采取离散化的技巧, 把每一个建筑物的两个\(x\)坐标去重排序存放到一个数组中,这样就得到了有限个线段区间, 因为包含了所有矩形的\(x\)坐标，因此，相邻两点之间对于任意一个矩形来说，必定是完全的可见或者不可见, 我们可以用区间的中点来代表这段区间, 然后只需要对建筑物\(i\)枚举所有的区间, 依次判断建筑物\(i\)在该区间是否可见.

• 何判断一个矩形在当前线段区间可见呢?
  1.一个矩形\(A\)会被挡住当且仅当存在满足以下三点的矩形\(B\)：
  2.其\(y\)坐标小于当前矩形\(A\)的\(y\)坐标
  3.当前线段区间包含于矩形\(B\)的横坐标区间

C++代码

#include<bits/stdc++.h>

using namespace std;

const int N = 110;

struct Building
{
    int id;
    double x, y, w, d, h;
    bool operator < (const Building& t) const
	{
        if (x != t.x) return x < t.x;
        return y < t.y;
    }
}b[N];

int n;

bool cover(int i, double midx) //判断建筑i是否能够覆盖midx所在的区间 
{
	return (b[i].x <= midx && b[i].x + b[i].w >= midx);
}

bool isVisible(int i, double midx) //判断建筑i在midx所在区间是否可见 
{
    if (!cover(i, midx)) return false; //不在区间 
    for (int j = 0; j < n; j ++) //枚举建筑物 
	{
		//如果有建筑物比建筑i更高 && y更小 && 存在于此区间，建筑i就被挡住了 
        if (b[j].h >= b[i].h && b[j].y < b[i].y && cover(j, midx)) return false; // 建筑i被j挡住
    }
    
    return true; //不被挡住 
}

int main()
{
	int T = 0;
    while (cin >> n && n != 0)
	{
        if (T != 0) puts(""); //相邻测试输出的空行 
        printf("For map #%d, the visible buildings are numbered as follows:\n", ++ T);
        set<double> setx;
        for (int i = 0; i < n; i ++)
		{
            scanf("%lf %lf %lf %lf %lf", &b[i].x, &b[i].y, &b[i].w, &b[i].d, &b[i].h);
            b[i].id = i + 1;
            //将每一个建筑的两个x坐标先用set实现排序+去重，然后存储到x数组中，实现离散化 
            setx.insert(b[i].x);
			setx.insert(b[i].x + b[i].w);
        }
        
        sort(b, b + n);
        
		vector<double> x(setx.begin(), setx.end());
        int cnt = 0; //控制输出
        for (int i = 0; i < n; i ++) //枚举所有建筑 
		{
            for (int j = 0; j < x.size() - 1; j ++ ) //对于每一个建筑枚举所有的线段 
			{
                if (isVisible(i, (x[j] + x[j + 1]) / 2)) //取线段中点代表区间 
				{
                    cnt ++ ;
                    printf("%s%d", cnt != 1 ? " ":"", b[i].id); //前置空格
                    break;
                }
            }
        }
        puts("");
    }
    
    return 0;
}

---